Муниципальное бюджетное общеобразовательное учреждение
Красненская основная общеобразовательная школа
п. Красное Брасовского района
Брянской области
Рассмотрено:
на заседании МО учителей
Протокол №_____от_____________.
|
| Утверждаю: Директор МБОУ Красненская оош ________________ В.П.Митрахова Приказ № ______от______________ |


![]()
2017-2018учебный год

Автор-составитель:
Баранова И.В., учитель
математики
п. Красное 2017
Пояснительная записка
С учетом целей обучения в основной школе контрольно-измерительные материалы экзамена в новой форме проверяют сформированность комплекса умений, связанных с информационно-коммуникативной деятельностью, с получением, анализом, а также применением эмпирических знаний.
В связи с тем, что ЕГЭ по математике с 2009 года является обязательным для всех выпускников школ, Государственная итоговая аттестация за курс основной школы выдержана в идеологии единого подхода к общей математической подготовке обучающихся.
Структура экзаменационной работы и организация проведения экзамена отличаются от традиционной системы аттестации, поэтому и подготовка к экзамену должна быть другой.
В школах подготовка к экзаменам осуществляется на уроках, а также во внеурочное время на индивидуальных и групповых занятиях.
Для качественной подготовки к экзамену из школьного компонента выделен час на развивающий курс, который позволяет расширить и углубить изучаемый материал по школьному курсу.
Данный курс имеет основное назначение – введение открытой, объективной независимой процедуры оценивания учебных достижений обучающихся, результаты которой будут способствовать осознанному выбору дальнейшего пути получения образования; развивает мышление и исследовательские знания обучающихся; формирует базу общих универсальных приемов и подходов к решению заданий соответствующих типов. Экзаменационные материалы реализуют современные подходы к построению измерителей, они обеспечивают более широкие по сравнению с действующим экзаменом дифференцирующие возможности, ориентированы на сегодняшние требования к уровню подготовки обучающихся.
Цели элективного курса: подготовить обучающихся к сдаче экзамена в форме ГИА в соответствии с требованиями, предъявляемыми новыми образовательными стандартами.
Задачи:
Повторить и обобщить знания по алгебре и геометрии за курс основной общеобразовательной школы;
Расширить знания по отдельным темам курса Алгебра 5-9 класс и Геометрия 7-9 класс;
Выработать умение пользоваться контрольно-измерительными материалами.
Рабочая программа элективного курсу «Математический практикум» ориентирована на учащихся 9 классов и реализуется на основе следующих документов:
Федеральный компонент государственного образовательного стандарта начального общего, основного общего и основного общего образования.
Федеральный базисный учебный план для основного общего образования.
Элективный курс «Математический практикум» изучается из расчета 1 час в неделю, всего 34 часа.
Составленное календарно-тематическое планирование соответствует содержанию программ основного общего образования по математике и обеспечивает выполнение требований государственного стандарта математического образования. Включенный в программу материал предполагает повторение и углубление следующих разделов:
Проценты
Выражения и их преобразования
Уравнения и системы уравнений
Неравенства
Функции
Текстовые задачи
Геометрия
Формы проведения занятий включают в себя лекции, практические работы, тренинги по использованию методов поиска решений.
Основной тип занятий комбинированный урок. Каждая тема курса начинается с постановки задачи. Теоретический материал излагается в форме мини лекции. После изучения теоретического материала выполняются практические задания для его закрепления. Занятия строятся с учётом индивидуальных особенностей обучающихся, их темпа восприятия и уровня усвоения материала.
В ходе обучения периодически проводятся непродолжительные, рассчитанные на 30-45 минут, контрольные работы и тестовые испытания для определения глубины знаний и скорости выполнения заданий. Контрольные замеры обеспечивают эффективную обратную связь, позволяющую обучающим и обучающимся корректировать свою деятельность.
Систематическое повторение способствует более целостному осмыслению изученного материала, поскольку целенаправленное обращение к изученным ранее темам позволяет обучающимся встраивать новые понятия в систему уже освоенных знаний.
Контроль и система оценивания Текущий контроль уровня усвоения материала осуществляется по результатам выполнения обучающимися самостоятельных, практических и лабораторных работ. Присутствует как качественная, так и количественная оценка деятельности.
Качественная оценка базируется на анализе уровня мотивации обучающихся, их общественном поведении, самостоятельности в организации учебного труда, а так же оценке уровня адаптации к предложенной жизненной ситуации (сдачи экзамена по алгебре в форме малого ЕГЭ).
Количественная оценка предназначена для снабжения обучающихся объективной информацией об овладении ими учебным материалом и производится по пятибалльной системе.
Итоговый контроль реализуется в двух формах: традиционного зачёта и тестирования.
Требования к уровню подготовки
В результате работы по программе учащиеся должны:
Знать:
методы проверки правильности решения заданий;
методы решения различных видов уравнений и неравенств;
основные приемы решения текстовых задач, а также проверки правильности ответов;
элементарные методы исследования функции.
методы нахождения статистических характеристик
методы решения геометрических задач
Уметь:
проводить преобразования в степенных, дробно-рациональных выражениях;
решать уравнения и неравенства различного типа;
применять свойства арифметической и геометрической прогрессий;
решать различные текстовые задачи;
решать комбинаторные задачи
находить вероятности случайных событий в простейших случаях
использовать приобретенные знания в различных жизненных ситуациях, практической деятельности.
уметь распознавать геометрические фигуры, различать взаимное расположение, изображать геометрические фигуры, выполнять чертежи по условию задачи.
Содержание программы курса
Проценты
Решение задач на проценты. Сложный процент.
Числа и выражения. Преобразование выражений
Свойства арифметического квадратного корня. Стандартный вид числа. Формулы сокращённого умножения. Приёмы разложения на множители. Выражение переменной из формулы. Нахождение значений переменной.
Уравнения
Способы решения различных уравнений (линейных, квадратных и сводимых к ним, дробнорациональных и уравнений высших степеней).
Системы уравнений
Различные методы решения систем уравнений (графический, метод подстановки, метод сложения). Применение специальных приёмов при решении систем уравнений.
Неравенства
Способы решения различных неравенств (числовых, линейных, квадратных). Метод интервалов. Область определения выражения. Системы неравенств.
Функции
Функции, их свойства и графики (линейная, обратнопропорциональная, квадратичная и др.) «Считывание» свойств функции по её графику. Анализирование графиков, описывающих зависимость между величинами. Установление соответствия между графиком функции и её аналитическим заданием.
Текстовые задачи
.Задачи на «движение», на «концентрацию», на «смеси и сплавы», на «работу». Задачи геометрического содержания.
Уравнения и неравенства
Модуль числа, его геометрический смысл, основные свойства модуля. Уравнения и неравенства, содержащие знак модуля и способы их решения.
Линейные и квадратные уравнения и неравенства с параметром, способы их решения. Применение теоремы Виета. Расположение корней квадратного уравнения относительно заданных точек. Системы линейных уравнений.
Геометрия
Параллельные прямые. Треугольник. Четырехугольник. Окружность.
Обобщающее повторение. Решение заданий КИМов ГИА
Решение задач из контрольно измерительных материалов для ГИА.
Календарно - тематическое планирование (9 класс)
(1 час в неделю, всего 35 ч)
| № урока | Название раздела Тема урока | Кол-во часов |
Содержание урока
| Основные знания, умения, навыки | Дата | ||
| план | факт | ||||||
| Числа и выражения. Преобразование выражений (2 часа) | |||||||
| | Формулы сокращённого умножения. Приёмы разложения на множители. | 1 | Выражения и их преобразования. Многочлен. Формулы | Знать:
Уметь:
|
|
| |
| | Выражение переменной из формулы. Нахождение значений переменной. | 1 |
|
| |||
| Уравнения (2 часа) | |||||||
| | Способы решения различных квадратных и сводимых к ним уравнений | 1 | Формула корней квадратного уравнения. Целое рациональное уравнение. Степень целого уравнения . Биквадратное уравнение. Дробные рациональные уравнения | Уметь:
|
|
| |
| | Способы решения различных дробно-рациональных и уравнений высших степеней уравнений | 1 |
|
| |||
| Системы уравнений (2 часа) | |||||||
| | Графический метод решения систем уравнений | 1 | Метод подстановки. Метод сложения. Способы решения систем уравнений второй степени. Графический метод решения систем уравнений. | Уметь:
|
|
| |
| | Различные методы решения систем уравнений (метод подстановки, метод сложения). | 1 |
|
| |||
| Неравенства (2 часа) | |||||||
| | Способы решения различных неравенств (числовых, линейных, квадратных). Метод интервалов. Область определения выражения. | 1 | Понятие «решение неравенства», «решение системы неравенств», понятие «линейное неравенство. Решение неравенств второй степени с помощью графика. Алгоритм решения неравенств методом интервалов. | Знать:
Уметь:
|
|
| |
| | Системы неравенств. | 1 |
|
| |||
| Функции (1 часа) | |||||||
| | Функции, их свойства и графики Установление соответствия между графиком функции и её аналитическим заданием. | 1 | Функция, область определения, область значений, график функции. Нули функции, промежутки знакопостоянства. Графики функций. | Знать:
Уметь:
|
|
| |
| 1 | |||||||
| 1 | |||||||
| Текстовые задачи (2 часа) | |||||||
| | .Задачи на «движение», на «концентрацию», на «смеси и сплавы», на «работу». | 1 | Текстовая задача. Виды текстовых задач. Рисунки, схемы, таблицы, чертежи при решении задач. Арифметический и алгебраический способы решения текстовой задачи. Нестандартные способы решения текстовых задач. | Знать:
Уметь:
|
|
| |
| | Задачи геометрического содержания. | 1 |
|
| |||
| Геометрия (4 часа) | |||||||
| | Параллельные прямые. Треугольник. | 1 | Параллельные прямые. Треугольник. Четырехугольник. Окружность. Решение треугольником. Подобие фигур. Многоугольники | Уметь:
|
|
| |
| | Четырехугольник. Окружность. | 1 |
|
| |||
| | Решение треугольником. Подобие фигур. | 1 |
|
| |||
| | Многоугольники | 1 |
|
| |||
| Обобщающее повторение. Решение заданий КИМов ГИА (4 часов) | |||||||
| | Решение задач из контрольно- измерительных материалов для ГИА. | 1 |
|
|
|
| |
| | Решение задач из контрольно- измерительных материалов для ГИА. | 1 |
|
| |||
Список литературы
Алгебра: сб. заданий для подгот. к гос. итоговой аттестации в 9 кл. /[Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.].- 5-е изд. — М. : Просвещение, 2016..
Алгебра: сб. заданий для подгот. к гос. итоговой аттестации в 9 кл. /[Л. В. Кузнецова, С. Б. Суворова, Е. А. Бунимович и др.]. — 4-е изд., перераб. — М. : Просвещение, 2015.
Кузнецова Л. В., Суворова С. Б., Бунимович Е. А., Колесникова Т. В., Рослова Л. О. Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2017/ ФИПИ. — М.: Интеллект-Центр, 2010.
ГИА-2017 : Экзамен в новой форме : Алгебра 9-й кл. : Тренировочные варианты экзаменационных работ для проведения государственной итоговой аттестации в новой форме / авт.-сост. Л.В. Кузнецова, СБ. Суворова Е.А. Бунимович и др. — М.: ACT: Астрель, 2017.
И. В. Ященко, А. В. Семенов, П. И. Захаров Подготовка к экзамену по математике ГИА 9 (новая форма). - Методические рекомендации. - М., МЦНМО, 2016..
Математика. 9 класс. Подготовка к ГИА -2012: учебно-методическое пособие / Под ред. Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов –на-Дону: Легион-М. 2011.
Алгебра. 9-й класс. Подготовка к государственной итоговой аттестации-2017: учебно-методическое пособие / Под ред. Ф. Ф. Лысенко. —Ростов-на-Дону: Легион-М., 2009.
Колесникова Т.В., Минаева С.С. Типовые тестовые задания 9 класс. М.: «Экзамен», 2007..
Мордкович А.Г. Алгебра. Часть 1. Учебник. 79 классы. М.: «Мнемозина», 2004.
Алгебра. Решебник. 9 класс. Подготовка к государственной итоговой аттестации-2010. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю. —Ростов-на-Дону: Легион-М., 2009.
Глазков, Ю.А. ГИА. Алгебра. 9 класс. Государственная итоговая аттестация (в новой форме). Тематические тестовые задания / Ю.А. Глазков, М.Я. Гаиашвили. — М.: Издательство «Экзамен», 2010.

 Получите свидетельство
Получите свидетельство Вход
Вход



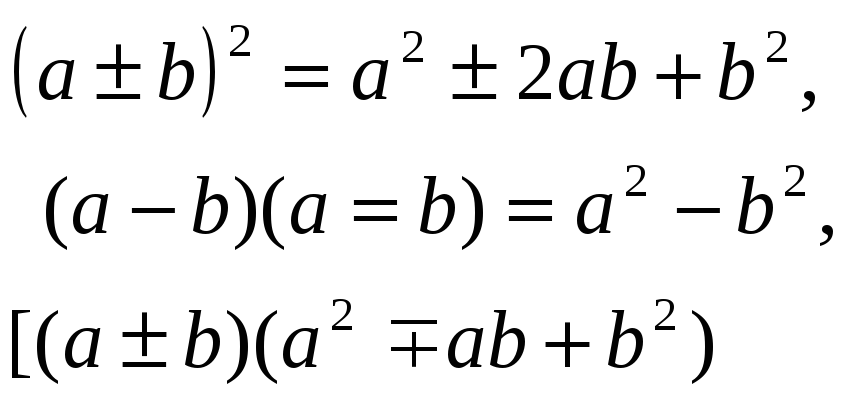









 Элективный курс "Математический практикум" (688.5 KB)
Элективный курс "Математический практикум" (688.5 KB)
 0
0 326
326 5
5 Нравится
0
Нравится
0


