МКУ «Департамент образования Местной администрации г.о. Нальчик»
Муниципальное казённое учреждение дополнительного образования
Центр детского творчества «Эрудит»
| Рассмотрена и одобрена на заседании Методсовета МКУ ДО ЦДТ «Эрудит» Протокол № ______ от «___» _____________ 2018 год | «Утверждаю» Директор МКУ ДО ЦДТ «Эрудит» _____________ М.А. Габаева «___» _____________ 2018 год |
ДОПОЛНИТЕЛЬНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА
«МАТЕМАТИЧЕСКИЕ СТУПЕНЬКИ»
Объединение: Математика
Срок реализации: 1 учебный год
Возраст: 11 - 14 лет
Автор: Шаваева Мадина Исмаиловна – педагог дополнительного образования
г.о. Нальчик
2018
Пояснительная записка
Дополнительная общеобразовательная программа «Математические ступеньки» составлена на основе федерального компонента государственного стандарта основного общего образования и конкретизирует содержание определенных тем образовательного стандарта.
Документы и материалы, с учетом которых составлена дополнительная общеобразовательная программа:
ФЗ-273 от 29.12.2012 г. «Об образовании в Российской Федерации».
Конвенция ООН о правах ребенка.
Программа развития на 2014-2019 г.г.
Порядок организации и осуществления образовательной деятельности по дополнительным общеобразовательным программам (Приказ Минобрнауки РФ №1008 от 29.08.2013г.)
Концепция развития дополнительного образования детей (Распоряжение Правительства РФ от 04.09.2014 г. №1726-р).
Образовательная программа учреждения.
Функциональные обязанности педагога дополнительного образования.
Устав Центра.
Данная дополнительная общеобразовательная программа «Математические ступеньки» рассчитана на обучающихся 11 - 14 лет. Программа составлена на основе федерального компонента государственного стандарта основного общего образования и конкретизирует содержание определенных тем образовательного стандарта и дает примерное распределение часов по разделам курса и выполняет две основные функции: информационно-методическую и организационно-планирующую.
Данный курс несет на себе нагрузку не только систематического развития понятия числа, выработки умений выполнять устно и письменно арифметические действия над числами, но и научить переводить практические задачи на язык математики, дать первоначальные понятия о геометрических фигурах, подготовка обучающихся к изучению алгебры и геометрии. Программа курса «Математические ступеньки» направлена на развитие одаренности у детей, углубление знаний учащихся, получаемых ими при изучении основного курса, развитие познавательного интереса к предмету, любознательности, смекалки, расширение кругозора. Программа строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил.
В ходе изучения курса обучающиеся развивают навыки вычислений с натуральными числами, овладевают навыками действий с обыкновенными и десятичными дробями, получают представления об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур и измерения геометрических величин.
Новизна программы определяется тем, что реализуется исследовательская деятельность обучающихся при решении нестандартных задач, проведение презентаций к докладам, решению логических задач, связанных с информатикой, теорией вероятности, осуществляется поиск, систематизация, классификация информации, использование разнообразных информационных источников.
Большое внимание уделяется решению нестандартных задач, проведению викторин, конкурсов, олимпиад, предоставлению возможности обучающимся продемонстрировать свои познания в области математики. Образование в современных условиях призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими компетентностного опыта в сфере учения, познания, профессионально-трудового выбора, личностного развития, ценностных ориентаций и смыслотворчества. Это предопределяет направленность целей обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределению в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.
Главной целью образования является развитие ребёнка как компетентной личности путём включения его в различные виды ценностной человеческой деятельности: учёба, познания, коммуникация, профессионально-трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определённой суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями.
Цель программы: Создание условий для интеллектуального развития обучающихся и формирования ценностно-смысловых компетенций школьников, с ориентацией на построение индивидуального образовательного маршрута. Привлечение к активным занятиям обучающихся, интересующих математикой.
Задачи курса:
Овладение, уточнение, закрепление знаний, полученных обучающимися в основной школе, связи с изучением смежных дисциплин.
Интеллектуальное развитие, формирование качеств личности, необходимых в современном обществе: ясность и точность мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей.
Формирование представлений об идеях и методах математики как универсального языка науки и техники.
Воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Изучение математики направлено на достижение следующих целей:
в направлении личностного развития:
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• формирование у обучающихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
• развитие интереса к математическому творчеству и математических способностей;
в метапредметном направлении:
• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
в предметном направлении:
• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Возраст детей, участвующих в реализации данной программы: 11-14 лет
Направленность программы: естественнонаучная
Тип программы: модифицированная
Режим и форма занятий
для обучающихся 13 и 14 лет - по 2 часа 2 раза в неделю (36 учебных недель) по утвержденному расписанию;
для обучающихся 11 и 12 лет – по 1 часу 2 раза в неделю (36 учебных недель) по утвержденному расписанию.
Длительность одного занятия 40 минут, перерыв на отдых 10 минут.
Основные формы и методы работы:
- лекционная;
практическая;
игровая;
групповая;
индивидуальная;
коллективная.
Ожидаемый результат:
Планируемые результаты освоения курса:
Изучение курса математики по данной программе способствует формированию у учащихся личностных, метапредметных и предметных результатов обучения, соответствующих требованиям федерального государственного образовательного стандарта основного общего образования.
в личностном направлении:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
уметь распознавать логически некорректные высказывания, отличать гипотезу от факта, вырабатывать критичность мышления;
представлять математическую науку как сферу человеческой деятельности, представлял этапы её развития и значимость для развития цивилизации;
вырабатывать креативность мышления, инициативу, находчивость, активность при решении математических задач;
уметь контролировать процесс и результат учебной математической деятельности;
вырабатывать способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
в метапредметном направлении:
иметь первоначальные представления об идеях и методах математики как об универсальном языке науки и техники, о средствах моделирования явлений и процессов;
уметь видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
уметь находить в различных источниках информацию, необходимую для решения математических проблем и представлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
уметь понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
уметь выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
уметь применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимать сущность алгоритмических предписаний и уметь действовать в соответствии с предложенным алгоритмом;
уметь самостоятельно ставить цели, выбирать и создавать алгоритм для решения учебных математических проблем;
уметь планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
в предметном направлении:
уметь работать с математическим текстом (структурирование, извлечение необходимой информации);
владеть базовым понятийным аппаратом:
развитие представлений о числе;
овладеть базовыми понятиями по основным разделам содержания; представлениями об основных изучаемых понятиях как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
усвоение на наглядном уровне знания о свойствах плоских и пространственных фигур; приобретение навыков их изображения и использования геометрического языка для описания предметов окружающего мира;
овладеть практически значимыми математическими умениями и навыками, их применением к решению математических и нематематических задач, предполагающих умение:
выполнять устные, письменные, инструментальные вычисления;
научиться решать текстовые задачи арифметическим способом, составлять графические и аналитические модели реальных ситуаций;
составлять алгебраические модели реальных ситуаций, решать простейшие линейные уравнения;
иметь представление о пропорциональных и обратно пропорциональных величинах, уметь составлять и решать пропорции;
использовать геометрический язык для описания предметов окружающего мира;
приобрести опыт измерения длин отрезков, длины окружности, величин углов, использовать формулы для нахождения периметров, площадей, объемов геометрических фигур, пути для вычисления значений неизвестной величины;
выполнять чертежи, делать рисунки, схемы по условию задачи;
уметь проводить несложные практические расчёты (включающие вычисления с процентами, выполнение необходимых измерений, использование прикидки и оценки);
уметь использовать буквы для записи общих утверждений, формул, выражений, уметь выполнять простейшие тождественные преобразования;
выполнять алгебраические преобразования для упрощения простейших буквенных выражений;
познакомиться с идеей координат на прямой и на плоскости; уметь выполнять стандартные процедуры на координатной плоскости;
иметь представление о достоверных, возможных, случайных событиях, о вероятности событий, уметь решать простейшие комбинаторные задачи.
К концу изучаемого курса обучающиеся 11 лет должны знать/уметь:
Натуральные числа и шкалы
уметь распознавать ряд натуральных чисел;
четко формулировать определения отрезка, длины отрезка, прямой, луча и уметь проводить их сравнительную характеристику при построении;
выполнять построения треугольника, находить площадь и периметр треугольника;
уметь сопоставлять координаты числам, отмеченным на шкале;
используя шкалу сравнивать натуральные числа;
Сложение и вычитания натуральных чисел
четко формулировать правила сложения и вычитания натуральных чисел, свойства;
♦ знать формулы, отражающие свойства сложения и вычитания, с переходом на буквенную запись, и применять их на практике.
♦ знать основные методы решения уравнения с одним неизвестным и выполнять проверку.
Умножение и деление натуральных чисел
знать свойства умножения и применять их на практике при работе с натуральными числами;
выполнять деление натуральных чисел нацело и с остатком;
выполнять возведение натурального числа в куб и квадрат;
♦ знать порядок выполнения действий при упрощении выражений;
Площади и объёмы
четко формулировать формулы площади и объема прямоугольника и прямоугольного параллелепипеда;
выполнять построение геометрических фигур;
уметь решать задачи по нахождению площади и объема прямоугольника и прямоугольного параллелепипеда.
Обыкновенные дроби
выполнять построения окружности при помощи циркуля;
давать определение окружности, кругу, долям, обыкновенным дробям
уметь сравнивать обыкновенные;
отличать правильную дробь от неправильной дроби;
выполнять сложение и вычитание дробей с одинаковыми знаменателями;
выполнять перевод смешанного числа в неправильную дробь и наоборот;
выполнять сложение и вычитание смешанных чисел;
Десятичные дроби
уметь записывать обыкновенную дробь в виде десятичных дробей;
знать основные правила сложения и вычитания десятичных дробей;
уметь сравнивать десятичные дроби;
уметь округлять десятичные дроби до целых, десятых, сотых и т.д.;
Умножение и деление десятичных дробей
знать основные правила умножения десятичных дробей на натуральные числа и применять их на практике;
выполнять деление десятичных дробей на натуральные числа;
выполнять умножение десятичных дробей;
выполнять деление на десятичную дробь;
находить среднее арифметическое чисел;
Инструменты для вычислений и измерений
знать работу микрокалькулятора и уметь пользоваться транспортиром.
К концу изучаемого курса обучающиеся 12 лет должны знать/уметь:
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты – в виде дроби и дробь – в виде процентов;
арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями и однозначным знаменателем и числителем;
выполнять арифметические действия с рациональными числами, сравнивать рациональные числа; находить значения числовых выражений;
решать текстовые задачи, включая задачи, связанные с отношением и пропорциональностью величин, дробями и процентами;
решать линейные уравнения и текстовые задачи при помощи них;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами;
строить геометрические фигуры и измерять геометрические величины.
Делимость чисел
Делители и кратные числа.
Признаки делимости на 2,3,5,10.
Простые и составные числа.
Разложение числа на простые множители.
Наибольший общий делитель.
Наименьшее общее кратное.
Находить делители и кратные числа.
Находить наибольший общий делитель двух или трех чисел.
Находить наименьшее общее кратное двух или трех чисел.
Сложение и вычитание дробей с разными знаменателями
Обыкновенные дроби.
Сократимая дробь.
Несократимая дробь.
Основное свойство дроби.
Сокращение дробей.
Сравнение дробей.
Сложение и вычитание дробей с разными знаменателями.
Сокращать дроби.
Приводить дроби к общему знаменателю.
Складывать и вычитать обыкновенные дроби с разными знаменателями.
Умножение и деление обыкновенных дробей
Умножение дробей.
Нахождение части числа.
Распределительное свойство умножения.
Взаимно обратные числа.
Нахождение числа по его части.
Находить число обратное данному.
Выполнять деление обыкновенных дробей.
Находить число по его дроби.
Находить значения дробных выражений
Умножать обыкновенные дроби.
Находить часть числа.
Отношения и пропорции
Отношения.
Пропорции.
Основное свойство пропорции.
Пропорциональные и обратно пропорциональные величины.
Формула длины окружности.
Формула площади круга.
Масштаб. Шар.
Составлять и решать пропорции.
Решать задачи с помощью пропорций на прямую и обратную пропорциональные зависимости.
Масштаб.
Длина окружности, площадь круга.
Шар.
Решать задачи по формулам.
Положительные и отрицательные числа
Противоположные числа.
Координаты на прямой.
Модуль числа.
Находить для числа противоположное ему число.
Находить модуль числа.
Сравнивать рациональные числа.
Сложение и вычитание положительных и отрицательных чисел
Правило сложения отрицательных чисел.
Правило сложения двух чисел с разными знаками.
Вычитание рациональных чисел
Сложение чисел с помощью координатной прямой.
Складывать числа с помощью координатной плоскости.
Складывать и вычитать рациональные числа.
Умножение и деление положительных и отрицательных чисел
Понятие рациональных чисел.
Выполнять умножение и деление рациональных чисел.
Свойства действий с рациональными числами.
Применять свойства действий с рациональными числами для преобразования выражений.
Решение уравнений
Подобные слагаемые.
Коэффициент выражения.
Правила раскрытия скобок.
Раскрывать скобки.
Приводить подобные слагаемые
Применять свойства уравнения для нахождения его решения.
Координаты на плоскости
Перпендикулярные прямые.
Параллельные прямые.
Координатная плоскость.
Координаты точки.
Столбчатая диаграмма.
График зависимости.
Изображать координатную плоскость.
Строить точку по заданным координатам.
Находить координаты изображенной в координатной плоскости точки.
Строить столбчатые диаграммы.
К концу изучаемого курса обучающиеся 13 лет должны знать/уметь:
по алгебре:
составлять буквенные выражения и формулы по условиям задач;
выполнять основные действия со степенями с целыми показателями;
выполнять действия с многочленами и алгебраическими дробями;
решать линейные уравнения, системы линейных уравнений;
решать текстовые задачи алгебраическим методом;
работать с координатной прямой и координатной плоскостью;
находить значение функции, заданной формулой, таблицей, графиком по ее аргументу и решать обратные задачи;
определять свойства функции по ее графику;
описывать свойства функции и строить графики.
по геометрии:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры, выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей, объемов);
решать геометрические задачи, опираясь на изученные свойства фигур;
проводить доказательные рассуждения при решении задач, используя известные теоремы;
пользоваться геометрическими инструментами (линейка, угольник, циркуль, транспортир).
К концу изучаемого курса обучающиеся 14 лет должны знать/уметь:
по алгебре:
производить все математические действия с алгебраическими дробями;
знать свойства функции у =
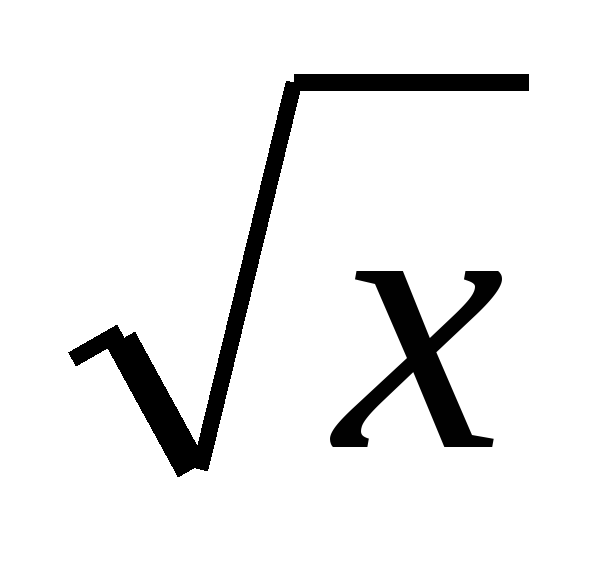 и свойства квадратного корня;
и свойства квадратного корня;знать свойства квадратичной функции и ее график;
решать линейные уравнения, системы линейных уравнений;
решать текстовые задачи алгебраическим методом;
работать с координатной прямой и координатной плоскостью и уметь строить графики функций;
находить значение функции, заданной формулой, таблицей, графиком по ее аргументу и решать обратные задачи;
определять свойства функции по ее графику;
уметь решать квадратные уравнения;
уметь решать квадратные неравенства методом интервалов.
по геометрии:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры, выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей, объемов);
решать геометрические задачи, опираясь на изученные свойства фигур;
проводить доказательные рассуждения при решении задач, используя известные теоремы;
пользоваться геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Формы подведения итогов:
самостоятельная работа;
собеседование;
тесты;
викторины;
математические игры и соревнования;
олимпиады.
Учебно-тематический план
/11 лет/
| № | Перечень разделов тем | Всего часов | Теория | Практика |
| 1 | Натуральные числа и шкалы. История возникновения чисел. | 2 | 1 | 1 |
| 2 | Делители числа. Признаки делимости, которые не изучают в школе. | 4 | 2 | 2 |
| 3 | Сложение и вычитание натуральных чисел. Нестандартные способы сложения и вычитания отрицательных и положительных чисел. | 6 | 3 | 3 |
| 4 | Умножение и деление натуральных чисел. | 5 | 2 | 3 |
| 5 | Площади и объемы. Решение задач, связанных с ремонтом в квартире.. | 4 | 2 | 2 |
| 6 | Обыкновенные дроби и их необыкновенное применение. | 11 | 4 | 7 |
| 7 | Десятичные дроби и умение их применять в повседневной жизни. | 6 | 2 | 4 |
| 8 | Умножение и деление десятичных дробей. Нестандартные способы вычислений. | 10 | 4 | 6 |
| 9 | Координатная плоскость в повседневной жизни.двухмерное и трехмерное пространство. | 5 | 2 | 3 |
| 10 | Инструменты для вычислений и измерений | 4 | 1 | 3 |
| 11 | Решение задач на логическое мышление | 15 | 6 | 9 |
|
| Итого
| 72 | 29 | 43 |
Содержание программы
Натуральные числа и шкалы – 2 часа
Обозначение натуральных чисел. Отрезок. Длина отрезка. Треугольник. Плоскость. Прямая. Луч. Шкалы и координаты. Меньше или больше.
Делители числа – 4 часа.
Признаки делимости на 10,5 и 2. Признаки делимости на 9 и 3. Простые и составные числа. Наибольший общий делитель. Взаимно простые числа.
Сложение и вычитание натуральных чисел – 6 часов.
Сложение натуральных чисел и его свойства. Вычитание. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания. Уравнения
Умножение и деление натуральных чисел – 5 часов.
Умножение натуральных чисел и его свойства. Деление. Деление с остатком. Упрощение выражений. Порядок выполнения действий. Квадрат и куб.
Площади и объемы – 4 часа.
Формулы. Площадь. Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объём прямоугольного параллелепипеда.
Обыкновенные дроби – 11 часов.
Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби. Сложение и вычитание дробей с одинаковыми знаменателями. Деление и дроби. Смешанные числа. Сложение и вычитание смешанных чисел.
Десятичные дроби – 6 часов.
Сложение и вычитание десятичных дробей. Десятичная запись дробных чисел. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Приближенные значения чисел. Округление чисел.
Умножение и деление десятичных дробей – 10 часов.
Умножение десятичных дробей на натуральные числа. Деление десятичных дробей на натуральные числа. Умножение десятичных дробей. Деление на десятичную дробь. Среднее арифметическое.
Координатная плоскость – 5 часов.
Координаты точек. Построение фигур по координатам точек.
Инструменты для вычислений и измерений – 4 часа.
Микрокалькулятор. Проценты. Угол. Прямой и развернутый угол. Чертёжный угол. Измерение углов. Транспортир. Круговые диаграммы.
Решение задач на логическое мышление – 15 часов.
Методическое обеспечение программы
| № п/п | Разделы и темы | Основные формы занятий | Методы | Оснащение занятий | Форма подведения итогов |
| 1. | Натуральные числа и шкалы | групповые индивидуальные | лекция беседа | дидактический материал | собеседование |
| 2. | Делители числа | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 3. | Сложение и вычитание натуральных чисел | групповые индивидуальные | лекция практика | дидактический материал | тест по теме |
| 4. | Умножение и деление натуральных чисел | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 5. | Площади и объемы | групповые индивидуальные | лекция практика | дидактический материал | тест по теме |
| 6. | Обыкновенные дроби | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 7. | Десятичные дроби | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 8. | Умножение и деление десятичных дробей | групповые индивидуальные | лекция практика | дидактический материал | тест по теме |
| 9. | Координатная плоскость | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 10. | Инструменты для вычислений и измерений | групповые индивидуальные | лекция практика | дидактический материал | собеседование |
| 11. | Решение задач на логическое мышление | групповые индивидуальные | лекция практика | дидактический материал | собеседование |
Учебно-тематический план
/12 лет/
| № | Содержание темы | Всего | Теория | Практика |
|
| Раздел I. Делимость чисел. Решение нестандартных задач по данной теме | 7 | 1,5 | 5,5 |
| 1 | Признаки делимости. | 2 | 1 | 1 |
| 2 | Простые и составные числа | 1 | 0,5 | 0,5 |
| 3 | Разложение на множители. НОД | 1 | - | 1 |
| 4 | Наименьшее общее кратное | 1 | - | 1 |
| 5 | Решение тестов по пройденным темам | 1 | - | 1 |
| 6 | Решение задач из сборника «Кенгуру» | 1 | - | 1 |
|
| Раздел П. Сложение и вычитание |
|
|
|
|
| дробей с разными знаменателями. Применение разных приемов для вычислений. | 6 | 1,5 | 4,5 |
| 1 | Основное свойство дроби | 1 | 1,5 | 0,5 |
| 2 | Сравнение дробей (НОЗ). «Сложение и вычитание дробей» | 1 | - | 1 |
| 3 | Сложение и вычитание смешанных чисел | 2 | 1 | 1 |
| 4 | Самостоятельная работа | 1 | - | 1 |
| 5 | Решение задач на логическое мышление | 1 | - | 1 |
|
| Раздел III. Умножение и деление | 8 | 3 | 5 |
|
| обыкновенных дробей. |
|
|
|
| 1 | Умножение дробей. Нахождение дроби от числа | 2 | 1 | 1 |
| 2 | Применение распределительного свойства умножения | 2 | 1 | 1 |
| 3 | Взаимнообратные числа. Деление дробей | 1 | - | 1 |
| 4 | Нахождение числа по его дроби | 2 | 1 | 1 |
| 5 | Дробные выражения. Решение задач. | 1 | - | 1 |
|
| Раздел IV. Отношения и пропорции. Золотое сечение. | 8 | 3 | 5 |
| 1 | Отношения. Решение задач | 2 | 1 | 1 |
| 2 | Пропорции | 2 | 1 | 1 |
| 3 | Прямая и обратная пропорциональные зависимости | 2 | 1 | 1 |
| 4 | Масштаб. Решение задач | 1 |
| 1 |
| 5 | Длина окружности и площадь круга. Шар | 1 |
| 1 |
|
| Раздел V. Рациональные числа. | 5 | 1 | 4 |
|
| Положительные и отрицательные |
|
|
|
|
| числа. История их возникновения. |
|
|
|
| 1 | Координаты на прямой. Противоположные числа | 1 | - | 1 |
| 2 | Модуль числа. Построение графиков | 1 | - | 1 |
| 3 | Сравнение чисел. Изменение величин | 2 | 1 | 1 |
| 4 | Решение задач олимпиадного характера | 1 | - | 1 |
|
| Раздел VI: Сложение и вычитание | 8 | 3 | 5 |
|
| положительных и отрицательных |
|
|
|
|
| чисел. Применение различных способов для вычисления. |
|
|
|
| 1 | Сложение чисел с помощью координатной прямой | 1 | - | 1 |
| 2 | Сложение отрицательных чисел | 2 | 1 | 1 |
| 3 | Сложение чисел с разными знаками | 2 | 1 | 1 |
| 4 | Вычитание рациональных чисел | 2 | 1 | 1 |
| 5 | Решение задач из сборника «Кенгуру» | 1 | - | 1 |
|
| Раздел VII. Умножение и деление | 8 | 3 | 5 |
|
| рациональных чисел |
|
|
|
| 1 | Умножение и деление положительных и отрицательных чисел | 3 | 1 | 2 |
| 2 | Понятие рационального числа | 2 | 1 | 1 |
| 3 | Свойства действий с рациональными числами | 2 | 1 | 1 |
| 4 | Решение логических задач | 1 | - | 1 |
|
| Раздел VIII. Решение уравнений. Решение нестандартных видов уравнений. | 6 | 2 | 4 |
| 1 | Раскрытие скобок. Коэффициент | 2 | 1 | 1 |
| 2 | Подобные слагаемые | 2 | 1 | 1 |
| 3 | Решение уравнений | 1 | - | 1 |
| 4 | Математический турнир | 1 | - | 1 |
|
| Раздел IX. Координаты на | 5 | 1 | 4 |
|
| плоскости. Кинотеатр. Координаты в повседневной жизни. |
|
|
|
| 1 | Перпендикулярные и параллельные прямые | 1 | - | 1 |
| 2 | Координатная плоскость. Столбчатые диаграммы | 1 | - | 1 |
| 3 | Графики | 2 | 1 | 1 |
| 4 | Самостоятельная работа | 1 | - | 1 |
|
| Раздел X. Повторение | 11 | - | 11 |
|
| ИТОГО: | 72 | 19 | 53 |
Содержание программы
I. Делимость чисел – 7 часов.
Делители и кратные. Признаки делимости на 10, 5, 2. Признаки делимости, Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное.
Основная цель - сформулировать умения и навыки нахождения НОД и НОК, используя признаки делимости чисел. Продолжать формирование умения решать задачи и выполнять все действия с рациональными числами.
II. Сложение и вычитание дробей с разными знаменателями - 6 часов.
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел.
Основная цель - сформировать умения и навыки сложения и вычитания дробей с разными знаменателями.
III. Умножение и деление обыкновенных дробей – 8 часов.
Умножение дробей. Нахождение дроби от числа. Решение задач на нахождение дроби от числа. Применение распределительного свойства умножения. Взаимообратные числа. Деление дробей. Нахождение числа по его дроби. Дробные выражения.
Основная цель - изучив умножение и деление дробей, научить решать задачи на нахождение дроби от числа по его дроби.
IV. Отношения и пропорции – 8 часов.
Отношения. Решение задач. Пропорции. Прямая и обратная пропорциональные зависимости. Масштаб. Решение задач. Длина окружности и площадь круга. Шар.
V. Рациональные числа. Положительные и отрицательные числа – 5 часов.
Координаты на прямой. Противоположные числа. Модуль числа. Построение графиков. Сравнение чисел. Изменение величин.
Основная цель - сформировать понятие о модуле. Используя это понятие, показать детям графическое истолкование модуля.
VI. Сложение и вычитание положительных и отрицательных чисел - 8 часов.
Сложение чисел с помощью координатной прямой. Сложение отрицательных чисел. Сложение чисел с разными знаками. Вычитание.
Основная цель - выработать умения выполнять действия сложения и вычитания с рациональными числами.
VII. Умножение и деление рациональных чисел – 8 часов.
Умножение и деление положительных и отрицательных чисел. Понятие рационального числа. Свойства действий с рациональными числами. Самостоятельная работа по данной теме. Решение логических задач.
VIII. Решение уравнений – 6 часов
Раскрытие скобок. Коэффициент. Подобные слагаемые. Решение уравнений. Проведение математического турнира.
IX. Координаты на плоскости – 5 часов
Перпендикулярные и параллельные прямые. Координатная плоскость. Столбчатые диаграммы. Графики. Самостоятельная работа.
X. Повторение – 11 часов.
Методическое обеспечение программы
/12 лет/
| № п/п | Разделы и темы | Основные формы занятий | Методы работы | Оснащение занятий | Форма подведения итогов |
| 1. | Делимость чисел | групповые индивидуальные | лекция беседа | дидактический материал | Собеседование |
| 2. | Сложение и вычитание дробей с разными знаменателями | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 3. | Умножение и деление обыкновенных дробей | групповые индивидуальные | лекция практика | дидактический материал | тест по теме |
| 4. | Отношения и пропорции | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 5. | Рациональные числа. Положительные и отрицательные числа. | групповые индивидуальные | лекция практика | дидактический материал | тест по теме |
| 6. | Сложение и вычитание положительных и отрицательных чисел | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 7. | Умножение и деление рациональных чисел | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа |
| 8. | Решение уравнений | групповые индивидуальные | лекция практика | дидактический материал | самостоятельная работа викторина |
| 9. | Координаты на плоскости | групповые индивидуальные | лекция практика | дидактический материал | тест по теме |
| 10. | Повторение | групповые индивидуальные | лекция практика | дидактический материал | викторина тест по теме |
Учебно-тематический план алгебре
/13 лет/
| № n/n | Содержание темы | Количество часов | ||
| Всего | Теория | Практика | ||
| | Раздел I. Степень с натуральным показателем. Решение нестандартных задач. | 5 | 1 | 4 |
| | Понятие степени и свойства степени с натуральным показателем | 1 | - | 1 |
| | Умножение и деление степеней с одинаковыми основаниями, с одинаковыми показателями | 3 | 1 | 2 |
| | Степень с нулевым показателем | 1 | - | 1 |
| | Раздел II. Одночлены. Арифметические операции над одночленами. Решение нестандартных задач. | 10 | 2 | 8 |
| | Сложение и вычитание одночленов | 3 | 1 | 2 |
| | Умножение одночленов | 2 | - | 2 |
| | Возведение одночленов в натуральную степень | 3 | 1 | 2 |
| | Деление одночленов | 2 | - | 2 |
| | Раздел III. Многочлены. Арифметические операции над многочленами. Решение олимпиадных задач. | 16 | 3 | 13 |
| | Сложение и вычитание многочленов | 2 | - | 2 |
| | Умножение многочлена на одночлен | 2 | - | 2 |
| | Умножение многочлена на многочлен | 2 | - | 2 |
| | Формулы сокращенного умножения | 7 | 2 | 5 |
| | Деление многочлена на многочлен | 3 | 1 | 2 |
| | Раздел IV. Разложение многочленов на множители. Применение различных способов для разложения. | 20 | 3 | 17 |
| | Вынесение общего множителя за скобки | 4 | 1 | 3 |
| | Способ группировки | 5 | 2 | 3 |
| | Разложение многочлена на множители с помощью формул сокращенного умножения | 3 | - | 3 |
| | Комбинированные примеры, связанные с разложением многочлена на множители | 4 | - | 4 |
| | Сокращение алгебраических дробей | 4 | - | 4 |
| | Раздел V. Линейная функция и ее применение в повседневной жизни. | 10 | 2 | 8 |
| | Координатная прямая и координатная плоскость | 1 | - | 1 |
| | Линейное уравнение с двумя переменными и его график | 3 | 1 | 2 |
| | Линейная функция и ее график | 2 | - | 2 |
| | Прямая пропорциональность и ее график | 1 | - | 1 |
| | Взаимное расположение графиков линейных функций | 3 | 1 | 2 |
| | Раздел VI. Функция y = x2 | 7 | 3 | 4 |
| | Функция y = x2 и ее график | 3 | 1 | 2 |
| | Графическое решение уравнений | 4 | 2 | 2 |
| | Раздел VII. Системы двух линейных уравнений с двумя переменными. Решение нестандартных задач. | 15 | 2 | 13 |
| | Метод подстановки | 5 | 1 | 4 |
| | Метод алгебраического сложения | 5 | 1 | 4 |
| | Решение задач с помощью систем уравнения | 5 | - | 5 |
| | Раздел VIII. Повторение | 4 | - | 4 |
| | ИТОГО: | 87 | 16 | 71 |
Содержание изучаемого курса
по алгебре - 87 часов
Раздел I. Степень с натуральным показателем и ее свойства - 5 часов.
Понятие степени с натуральным показателем. Таблицы основных степеней. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковым показателем. Нулевой показатель.
Основные цели: Закрепить знания и умения по выполнению действий с натуральным показателем. Решение нестандартных задач по данной теме.
Раздел II. Одночлены. Арифметические операции над одночленами - 10 часов.
Понятие одночлена. Стандартный вид одночленов. Сложение и вычитание одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.
Основные цели: выработать у обучающихся практические навыки при работе с одночленами. Продолжать формировать умения решать нестандартные задачи.
Раздел III. Многочлены. Арифметические операции над многочленами - 16 часов.
Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Формулы сокращенного умножения. Деление многочлена на одночлен.
Основные цели: Выработать прочные навыки по работе с многочленами, уметь применять формулы сокращенного умножения.
Раздел IV. Разложение многочленов на множители - 20 часов.
Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения. Комбинированные примеры, связанные с разложением многочлена на множители. Сокращение алгебраических дробей.
Основные цели: Обеспечить овладение обучающимися умением выполнять разложение многочленов различными способами, выработать практические умения по данному вопросу.
Раздел V. Линейная функция - 10 часов.
Координатная прямая. Координатная плоскость. Линейное уравнение с двумя переменными и его график. Линейная функция и ее график. Прямая пропорциональность и ее график. Взаимное расположение графиков линейных функций.
Основные цели: Выработать умения строить графики линейных уравнений с двумя переменными, отработать эти умения.
Раздел VI. Функция у = х2 - 7 часов.
Функция у = х2 и ее график. Графическое решение уравнений.
Раздел VII. Системы двух линейных уравнений с двумя переменными - 15 часов.
Метод подстановки. Метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.
Основные цели: Научить обучающихся решать системы двух линейных уравнений с двумя переменными различными способами и применять системы при решении текстовых задач, олимпиадных задач.
Раздел VIII. Повторение - 4 часа.
Решение задач, занимательных упражнений из сборников нестандартных задач, сборников «Кенгуру».
Учебно-тематический план по геометрии
/13 лет/
| № n/n | Содержание темы | Количество часов | ||
| Всего | Теория | Практика | ||
| | Раздел I. Начальные геометрические сведения. История возникновения науки. | 7 | 2 | 5 |
| | Прямая и отрезок. Измерение отрезков | 1 | - | 1 |
| | Луч и угол. Измерение углов | 2 | 1 | 1 |
| | Перпендикулярные прямые, смежные и вертикальные углы | 3 | 1 | 2 |
| | Решение задач | 1 | - | 1 |
| | Раздел II. Треугольники. Египетский треугольник. | 14 | 3 | 11 |
| | Первый признак равенства треугольников | 3 | 1 | 2 |
| | Перпендикуляр к прямой медианы, биссектрисы и высоты треугольника | 3 | 1 | 2 |
| | Свойства равнобедренного треугольника | 2 | 1 | 1 |
| | Второй признак равенства треугольников | 1 | - | 1 |
| | Третий признак равенства треугольников | 1 | - | 1 |
| | Решение задач | 2 | - | 2 |
| | Задачи на построение | 2 | - | 2 |
| | Раздел III. Параллельные прямые. Решение задач из повседневной жизни. | 9 | 4 | 5 |
| | Определение параллельных прямых. Признаки параллельности двух прямых | 3 | 2 | 1 |
| | Аксиома параллельных прямых | 2 | 1 | 1 |
| | Свойства параллельных прямых | 2 | 1 | 1 |
| | Решение задач | 2 | - | 2 |
| | Раздел IV. Соотношение между сторонами и углами треугольника. Золотое правило треугольника. | 6 | 2 | 4 |
| | Теорема о сумме углов треугольника | 1 | - | 1 |
| | Внешний угол треугольника. Теорема о внешнем угле треугольника | 1 | - | 1 |
| | Теорема о соотношениях между сторонами и углами треугольника | 1 | 1 | - |
| | Неравенство треугольника | 1 | - | 1 |
| | Решение задач | 2 | 1 | 1 |
| | Раздел V. Прямоугольные треугольники. Решение нестандартных задач. | 10 | 2 | 8 |
| | Сумма двух острых углов прямоугольного треугольника. Прямоугольник с углом в 30 | 3 | 1 | 2 |
| | Признаки равенства прямоугольных треугольников | 3 | 1 | 2 |
| | Решение задач | 4 | - | 4 |
| | Раздел VI. Расстояние от точки до прямой. Измерения на местности. Решение задач на улице. | 7 | 1 | 6 |
| | Перпендикуляр и наклонная. Расстояние от точки до прямой | 2 | 1 | 1 |
| | Расстояние между параллельными прямыми | 1 | - | 1 |
| | Построение треугольника по трем элементам | 3 | - | 3 |
| | Решение задач | 1 | - | 1 |
| | Раздел VII. Повторение | 4 | - | 4 |
| | ИТОГО: | 57 | 14 | 43 |
Содержание изучаемого курса
по геометрии - 57 часов
Раздел I. Начальные геометрические сведения - 7 часов.
Точки, прямые, отрезки. Провешивание прямой на местности. Практические задания. Луч и угол. Сравнение отрезков и углов. Равенство геометрических фигур. Измерение отрезков (длина отрезка, единицы измерения). Измерение углов. Градусная мера. Измерение углов на местности. Перпендикулярные прямые. Смежные и вертикальные углы.
Выполнение практических заданий. Решение дополнительных задач.
Основные цели: Познакомить обучающихся с возникновением геометрии, с геометрическими фигурами, которые изучает геометрия, с основными понятиями, систематизировать сведения о взаимном расположении точек и прямых, ввести понятия углов, отрезков, их измерении, видах углов.
Раздел II. Треугольники - 14 часов.
Первый признак равенства треугольников. Практические задания. Дополнительные задания. Медианы, биссектрисы и высоты треугольника. Равнобедренные и равносторонние треугольники. Свойства равнобедренного треугольника. Решение дополнительных задач.
Второй признак равенства треугольников. Третий признак равенства треугольников. Решение задач.
Задачи на построение. Окружность. Построение циркулем и линейкой. Примеры задач на построение. Решение задач.
Основные цели: Ввести понятие треугольника и его элементов, решать задачи, развивать логическое мышление, разъяснить понятие теоремы и ее доказательство, выработать умение применять при решении задач признаки равенства треугольников и свойства равнобедренных треугольников.
Раздел III. Параллельные прямые - 9 часов.
Определение параллельных прямых. Признаки параллельности двух прямых. Практические способы построения параллельных прямых. Аксиома параллельных прямых. Свойства параллельных прямых. Решение задач.
Основные цели: Изучить признаки параллельности двух прямых, продолжать прививать навыки аккуратности в построении чертежей, продолжать решать задачи по изученной теме.
Раздел IV. Соотношения между сторонами и углами треугольника - 6 часов.
Теорема о сумме углов треугольника. Остроугольный, прямоугольный и тупоугольный треугольники. Внешний угол треугольника. Теорема о внешнем угле треугольника. Внешний угол треугольника. Теорема о внешнем угле треугольника. Теорема о соотношениях между сторонами и углами треугольника. Неравенство треугольника. Решение задач.
Основные цели: Усвоение теоремы о сумме углов треугольника и применять ее при решении задач. Ввести понятие внешнего угла треугольника, научить применять изученный теоретический материал при решении задач.
Раздел V. Прямоугольные треугольники - 10 часов.
Сумма двух острых углов прямоугольного треугольника. Прямоугольный треугольник с углом в 30º. Признаки равенства прямоугольных треугольников. Решение задач.
Основные цели: Научить применять свойства прямоугольных треугольников, признаки их равенства при решении задач.
Раздел VI. Расстояние от точки до прямой. Расстояние между параллельными прямыми - 6 часов.
Перпендикуляр и наклонная. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем измерениям. Решение задач. Множество точек, равноудаленных от данной прямой. Решение задач. Более сложные случаи построения треугольников.
Раздел VII. Итоговое повторение - 5 часов.
Учебно-тематический план по алгебре
/14 лет/
| № n/n | Содержание темы | Количество часов | ||
| Всего | Теория | Практика | ||
|
| Раздел I. Алгебраические дроби | 15 | 5 | 10 |
| | Основные понятия | 1 | - | 1 |
| | Основное свойство алгебраической дроби | 2 | 1 | 1 |
| | Сложение и вычитание алгебраических дробей с одинаковыми знаменателями | 2 | 1 | 1 |
| 4. | Сложение и вычитание алгебраических дробей с разыми знаменателями | 4 | 1 | 3 |
| 5. | Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень | 3 | 1 | 2 |
| 6. | Преобразование рациональных выражении | 2 | 1 | 1 |
| 7. | Степень с отрицательным целым показателем | 1 | - | 1 |
| | Раздел II. Функция | 10 | 2 | 8 |
| | Понятие квадратного корня из неотрицательного числа | 2 | 1 | 1 |
| | Функция | 3 | - | 3 |
| | Свойства квадратных корней | 3 | 1 | 2 |
| | Преобразование выражений, содержащих операцию извлечения квадратного корня | 2 | - | 2 |
| | Раздел III. Квадратичная функция. Функция | 20 | 6 | 14 |
| | Функция y =k x2, ее свойства и график | 3 | 1 | 2 |
| | Функция | 3 | 1 | 2 |
| | Как построить график функции y=f(x+l), если известен график функции у=f(x) | 3 | 1 | 2 |
| | Как построить график функции y=f(x)+m, если известен график функции у=f(x) | 4 | 1 | 3 |
| | Функция y= ах2 + bх + с ее свойства и график | 4 | 1 | 3 |
| | Графическое решение квадратных уравнений | 3 | 1 | 2 |
| | Раздел IV. Квадратные уравнения. | 17 | 4 | 13 |
| | Основные понятия | 3 | 1 | 2 |
| | Формулы корней квадратного уравнения | 5 | 2 | 3 |
| | Рациональные уравнения | 3 | - | 3 |
| | Рациональные уравнения как математические модели реальных ситуации | 4 | - | 4 |
| | Терема Виета | 2 | 1 | 1 |
| | Раздел V. Неравенства. | 20 | 7 | 13 |
| | Свойства числовых неравенств | 2 | 1 | 1 |
| | Исследование функции на монотонность | 3 | 1 | 2 |
| | Решение линейных неравенств | 4 | 1 | 3 |
| | Решение квадратных неравенств | 4 | 1 | 3 |
| | Иррациональные уравнения | 3 | 1 | 2 |
| | Приближенное значение действительных чисел | 2 | 1 | 1 |
| | Стандартный вид числа | 2 | 1 | 1 |
| | Раздел VIII. Повторение | 5 | - | 5 |
| | ИТОГО: | 87 | 24 | 63 |
Содержание изучаемого курса
по алгебре - 87 часов
Раздел I. Алгебраические дроби - 15 часов.
Основные понятия. Основное свойство алгебраической дроби. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Сложение и вычитание алгебраических дробей с разыми знаменателями. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Преобразование рациональных выражении. Первые представления о рациональных уравнениях. Степень с отрицательным целым показателем.
Основные цели: Закрепить знания и умения по выполнению действий с алгебраическими дробями. Решение нестандартных задач по данной теме.
Раздел II. Функция ![]() . Свойства квадратного корня – 10 часов.
. Свойства квадратного корня – 10 часов.
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Функция ![]() , ее свойства и график. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Модуль действительного числа, график функции
, ее свойства и график. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Модуль действительного числа, график функции ![]() , формула
, формула ![]() .
.
Основные цели: выработать у учащихся практические навыки при работе с корнями квадратными. Продолжать формировать умения решать нестандартные задачи.
Раздел III. Квадратичная функция. Функция ![]() - 20 часов.
- 20 часов.
Функция y =k x2, ее свойства и график. Функция ![]() , ее свойства и график. Как построить график функции y=f(x+l), если известен график функции у=f(x). Как построить график функции y=f(x)+m, если известен график функции у=f(x). Как построить график функции y=f(x+l)+m, если известен график функции у=f(x). Функция y= ах2 + bх + с ее свойства и график. Графическое решение квадратных уравнений.
, ее свойства и график. Как построить график функции y=f(x+l), если известен график функции у=f(x). Как построить график функции y=f(x)+m, если известен график функции у=f(x). Как построить график функции y=f(x+l)+m, если известен график функции у=f(x). Функция y= ах2 + bх + с ее свойства и график. Графическое решение квадратных уравнений.
Основные цели: Выработать прочные навыки по работе с графиками квадратичных функций.
Раздел IV. Квадратные уравнения - 20 часов.
Основные понятия. Формулы корней квадратного уравнения. Рациональные уравнения. Рациональные уравнения как математические модели реальных ситуации. Еще одна формула корней квадратного уравнения. Терема Виета .
Основные цели: Обеспечить овладение учащимися умением решать квадратные уравнения различными способами, выработать практические умения по данному вопросу.
Раздел V. Неравенства - 20 часов.
Свойства числовых неравенств. Исследование функции на монотонность. Решение линейных неравенств. Решение квадратных неравенств. Иррациональные уравнения. Приближенное значение действительных чисел. Стандартный вид числа.
Основные цели: Выработать умения решать квадратные неравенства методом интервалов. Иметь представление об иррациональных уравнениях.
Раздел VIII. Повторение - 5 часов.
Решение задач, занимательных упражнений из сборников нестандартных задач, сборников «Кенгуру».
Учебно-тематический план по геометрии
/14 лет/
| № n/n | Содержание темы | Количество часов | ||
| Всего | Теория | Практика | ||
|
| Раздел I. Четырехугольники | 13 | 4 | 9 |
| | Понятие многоугольника | 1 | - | 1 |
| | Параллелограмм | 1 | - | 1 |
| | Признаки параллелограмма | 2 | 1 | 1 |
| | Решение задач | 1 | - | 1 |
| | Трапеция | 2 | 1 | 1 |
| | Теорема Фалеса | 1 | - | 1 |
| | Прямоугольник | 2 | 1 | 1 |
| | Ромб и квадрат | 2 | 1 | 1 |
| | Решение задач | 1 | - | 1 |
| | Раздел II. Площадь | 13 | 6 | 7 |
| | Площадь многоугольника | 1 | 1 | - |
| | Площадь прямоугольника и квадрата | 2 | 1 | 1 |
| | Площадь параллелограмма | 2 | 1 | 1 |
| | Площадь треугольника | 2 | 1 | 1 |
| | Площадь трапеции | 2 | 1 | 1 |
| | Теорема Пифагора | 2 | 1 | 1 |
| | Решение задач | 2 | - | 2 |
| | Раздел III. Признаки подобия треугольников | 9 | 5 | 4 |
| | Определение подобных треугольников | 1 | 1 | - |
| | Отношение площадей подобных треугольников | 2 | 1 | 1 |
| | Первый признак подобия | 2 | 1 | 1 |
| | Второй признак подобия | 2 | 1 | 1 |
| | Третий признак подобия | 2 | 1 | 1 |
| | Раздел IV. Применение подобия к доказательству теорем и решению задач | 4 | 1 | 3 |
| | Средняя линия треугольника | 1 | - | 1 |
| | Свойство медиан треугольника | 1 | - | 1 |
| | Пропорциональные отрезки в прямоугольном треугольнике | 1 | 1 | - |
| | Решение задач | 1 | - | 1 |
| | Раздел V. Соотношения между сторонами и углами прямоугольного треугольника | 6 | 3 | 3 |
| | Синус, косинус и тангенс острого угла прямоугольного треугольника | 2 | 1 | 1 |
| | Значения синуса, косинуса и тангенса для углов 30, 45 и 60 | 2 | 1 | 1 |
| | Соотношения между сторонами и углами прямоугольного треугольника | 2 | 1 | 1 |
| | Раздел VI. Окружность | 12 | 2 | 10 |
| | Взаимное расположение прямой и окружности | 1 | - | 1 |
| | Касательная к окружности | 1 | - | 1 |
| | Теорема о вписанном угле | 1 | - | 1 |
| | Теорема об отрезках пересекающихся хорд | 1 | - | 1 |
| | Свойства биссектрисы угла | 1 | - | 1 |
| | Серединный перпендикуляр к отрезку | 1 | - | 1 |
| | Вписанная окружность. Свойство описанного четырёхугольника. | 2 | 1 | 1 |
| | Описанная окружность. Свойство вписанного четырёхугольника. | 2 | 1 | 1 |
| | Решение задач «Окружность» | 2 | - | 2 |
| | ИТОГО: | 57 | 21 | 36 |
Содержание изучаемого курса
по геометрии - 57 часов
Раздел I. Четырехугольники – 13 часов.
Многоугольник, выпуклый и невыпуклый многоугольник, формула суммы углов выпуклого многоугольника, периметр многоугольника. Параллелограмм. Свойства и признаки параллелограмма. Трапеция, виды трапеций, равнобедренная трапеция. Теорема Фалеса. Прямоугольник, свойства и признаки. Ромб, квадрат; свойства и признаки.
Выполнение практических заданий. Решение дополнительных задач.
Основные цели: Познакомить обучающихся с видами четырехугольников, разобрать их свойства и признаки.
Раздел II. Площадь – 13 часов
Формула для вычисления площади многоугольника. Формула для вычисления площади прямоугольника. Формула для вычисления площади прямоугольника. Формула для вычисления площади треугольника. Формула для вычисления площади трапеции. Теорема Пифагора. Теорема, обратная теореме Пифагора.
Основные цели: Ввести понятие площади четырехугольника, решать задачи, развивать логическое мышление, разъяснить понятие теоремы и ее доказательство, выработать умение применять при решении задач признаки равенства треугольников и свойства равнобедренных треугольников.
Раздел III. Признаки подобия треугольников – 9 часов
Пропорциональные отрезки, сходственные стороны, подобные треугольники. Первый признак подобия треугольников. Применение первого признака подобия. Второй и третий признаки подобия треугольников. Признаки подобия треугольников и их применение.
Основные цели: Изучить признаки подобия треугольников, продолжать решать задачи по изученной теме.
Раздел IV. Применение подобия к доказательству теорем и решению задач -4 часа.
Средняя линия треугольника. Свойство медиан треугольника. Пропорциональные отрезки в прямоугольном треугольнике. Практические приложения подобия треугольников .
Основные цели: Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике. Уметь доказывать эти теоремы и применять при решении задач , а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение.
Раздел V. Соотношения между сторонами и углами прямоугольного треугольника – 6 часов
Синус, косинус и тангенс острого угла прямоугольного треугольника. Значения синуса, косинуса и тангенса для углов 30, 45 и 60.
Основные цели: Знать определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30, 45 и 60, метрические соотношения. Уметь доказывать основное тригонометрическое тождество.
Раздел VI. Окружность – 12 часов.
Случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной. Центральный угол, вписанный угол, градусная мера дуги окружности, отрезки пересекающихся хорд.
Основные цели: Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной. Уметь их доказывать и применять при решении задач; выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.
Здоровьесберегающие технологии образовательного процесса
Данная инструкция обязательна для всех обучающихся. Обучающиеся должны знать основные правила техники безопасности на рабочем месте.
Прежде всего, это выполнение санитарно - гигиенических правил:
режим проветривания;
влажная уборка помещения;
соответствующая нормам освещенность;
соблюдение норм физических и умственных нагрузок.
Известно, что устойчивая работоспособность характерна для середины занятия. Этот момент необходимо учитывать при планировании. Необходимо чередовать различные виды деятельности и их последовательность для обеспечения функциональной активности основных систем организма в течение длительного времени. Для предупреждения перегрузок, переутомлений необходимо чаще проводить смену видов деятельности.
Образовательный процесс всегда связан с получением новой информации, которая лучше воспринимается, если задействованы различные каналы (кинетический, визуальный, аудиальный). Например, от просто прочитанного в памяти остается только 10% информации, от услышанного 20%, от увиденного 30%; от того, что слышим и видим 50%, от того, что используем в своей практической деятельности 90%. Отсюда вывод: необходимо использовать различные источники информации.
К здоровьесберегающим технологиям необходимо отнести обеспечение комфортного эмоционально-психического состояния обучающихся. Это помощь обучающимся в адаптации к новым условиям, создание общей эмоционально-положительной, дружественной, доверительной, доброй атмосферой на занятиях. Не следует забывать о создании «ситуации успеха», которая позволяет человеку находиться в состоянии психологического равновесия, исключая стрессы, обусловленные ошибками при выполнении задания, незнанием учебного материала.
Рекомендуемая литература для педагогов (5 класс):
Ганенкова И.С., «Математика» Многоуровневые самостоятельные работы в форме тестов для проверки качества знаний» 5-7 классы, 2001г.
Гальперин Г.А., Толпыго А.К., «Математические олимпиады в школе», М., 2004г.
Левитас Г.Г., «Математические диктанты» М: «Просвещение», 2005г.
Нагибин Ф.Ф., Канин Е.С., «Математическая шкатулка», 2003г.
Никольский С.М., Потапов М.К., «Математика», Пособие для самообразования, М., Наука. 2001г.
Симонов А.Я., Бакаев Д.С., Система тренировочных упражнений по математике», М., Просвещение, 2001г.
Чесноков А.С., «Дидактические материалы по математике» - М: «Просвещение» 2004г.
Рекомендуемая литература для педагогов (6 класс):
Ганенкова И.С., «Математика» Многоуровневые самостоятельные работы в форме тестов для проверки качества знаний» 5-7 классы, 2003г.
Гальперин Г.А., Толпыго А.К., «Математические олимпиады в школе», 2001г.
Левитас Г.Г., «Математические диктанты» М: «Просвещение» 2005г.
Нагибин Ф.Ф., Канин Е.С., «Математическая шкатулка», 2003г.
Никольский С.М., Потапов М.К., «Математика», пособие для самообразования. М., Наука. 2001г.
Симонов А.Я., Бакаев Д.С., Система тренировочных упражнений по математике», 2002
Чесноков А.С., «Дидактические материалы по математике» - М: «Просвещение» 2004г.
Рекомендуемая литература для обучающихся (5 класс):
Ганенкова И.С., «Математика» Многоуровневые самостоятельные работы в форме тестов для проверки качества знаний» 5-7 классы, 2001г.
Гальперин Г.А., Толпыго А.К., «Математические олимпиады в школе», М., 2004г.
Нагибин Ф.Ф., Канин Е.С., «Математическая шкатулка», 2003г.
Никольский С.М., Потапов М.К., «Математика», Пособие для самообразования, М., Наука. 2001г.
Симонов А.Я., Бакаев Д.С., Система тренировочных упражнений по математике», М., Просвещение, 2001г.
Чесноков А.С., «Дидактические материалы по математике» - М: «Просвещение» 2004г.
Рекомендуемая литература для обучающихся (6 класс):
Ганенкова И.С., «Математика» Многоуровневые самостоятельные работы в форме тестов для проверки качества знаний» 5-7 классы, 2003г.
Гальперин Г.А., Толпыго А.К., «Математические олимпиады в школе», 2001г.
Нагибин Ф.Ф., Канин Е.С., «Математическая шкатулка», 2003г.
Никольский С.М., Потапов М.К., «Математика», пособие для самообразования. М., Наука. 2001г.
Симонов А.Я., Бакаев Д.С., Система тренировочных упражнений по математике», 2002г.
Чесноков А.С., «Дидактические материалы по математике» - М: «Просвещение», 2004г.
Рекомендуемая литература по алгебре для обучающихся и педагогов (7 класс):
Бартенев Ф.А., Нестандартные задачи по алгебре. – М.: Просвещение, 2003г.
Дудницын, Тульчинская Ю.П. , Алгебра 7 класс, Контрольные работы. – М.: Мнемозина, 2001г.
Жохов В.И., Крайнева Л.Б., Уроки алгебры в 7 классе.
Кенгуру – сборник задач 2003-2010 год – математика для всех.
Мордкович А.Г., Алгебра 7 класс. Методическое пособие для учителя.
Мордкович А.Г., Алгебра. 7 класс.
Мейлер В.М., Дидактические материалы для 7 класса (по алгебре).
Фарков А.В., Математические олимпиады в школе 5-11 классы.
Рекомендуемая литература по геометрии для обучающихся и педагогов (7 класс):
Атанасян Л.С. и др., Задачи повышенной трудности на построение, Москва, 2004г.
Афанасьева Г.Л., Поурочные планы. Геометрия 7 класс, Москва, 2007г.
Зив Б.Г., Мейлер В.М. , Дидактические материалы по геометрии, Москва, 2004г.
Математические тесты (институт продуктивного обучения Российской академии образования) под редакцией Братусь Т.А., Жарковская Н.А. и др., Москва, 2007г.
Сборник задач «Кенгуру» - 2000-2010 год.
Мейлер В.М., Дидактические материалы для 7 класса (по геометрии).
Фарков А.В. , Математические олимпиады в школе.
Рекомендуемая литература по алгебре для обучающихся и педагогов (8 класс):
Галицкий М.Л. и др. Сборник задач по алгебре: 8-9 классы.
Дудницын Ю.П. и др. Алгебра. Тематические тесты. 8 класс
Звавич Л.И. и др. Алгебра. Дидактические материалы для 8 класса.
Жохов В.И. и др. Алгебра. Дидактические материалы для 8 класса.
Жохов В.И. и др. Уроки алгебры в 7, 8 и 9 классах. Поурочные разработки.
Кузнецова Л.В. и др. Государственная итоговая аттестация. Алгебра. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе.
Макарычев Ю.Н. и др. Алгебра. Дидактические материалы для 8 класса.
Макарычев Ю.Н. и др. Изучение алгебры, в 7-9 классах. Книга для учителя.
Макарычев Ю.Н. и др. Элементы статистики и теории вероятностей, 7-9 классы.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дополнительные главы к школьному учебнику, 8 и 9 классы.
Ткачева М.В. и др. Сборник задач по алгебре для 7-9 классов.
Рекомендуемая литература по геометрии для обучающихся и педагогов (8 класс):
Атанасян Л.С. и др., Задачи повышенной трудности на построение, Москва, 2004г
Атанясан Л.С. и др., Геометрия 7-9 класс (учебник).
Афанасьева Г.Л., Поурочные планы. Геометрия 8 класс, Москва, 2007г.
Зив Б.Г., Мейлер В.М. , Дидактические материалы по геометрии, Москва, 2004г.Геометрия, 7 – 9: Учеб. для общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2004.
Б.Г. Зив, В.М. Мейлер, А.П. Баханский. Задачи по геометрии для 7 – 11 классов. – М.: Просвещение, 2003.
С.М. Саакян, В.Ф. Бутузов. Изучение геометрии в 7-9 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2001.
Научно-теоретический и методический журнал «Математика в школе»
31

 Получите свидетельство
Получите свидетельство Вход
Вход












 Дополнительная образовательная программа по математике (473.5 KB)
Дополнительная образовательная программа по математике (473.5 KB)
 0
0 1312
1312 116
116 Нравится
0
Нравится
0


