Действующее значение силы тока и напряжения

Презентация по физике для проведения урока по теме:

R , C , L в цепи переменного тока

Вопросы для изучения:

• Действующие значения тока и напряжения. Активное сопротивление в цепи ~ тока
• Конденсатор в цепи ~ тока
• Индуктивность в цепи ~ тока
• Использование частотных свойств конденсатора и катушки индуктивности

R C L

в цепи переменного тока -1

@ Краснополянская школа № 1 Домнин Константин Михайлович 2006 год

• Действующие значения тока и напряжения. Активное сопротивление в цепи переменного тока

Действующие значения тока и напряжения, виды сопротивлений

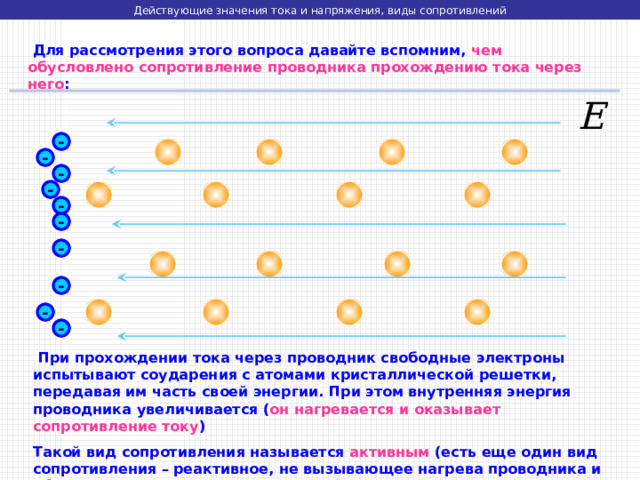
Для рассмотрения этого вопроса давайте вспомним, чем обусловлено сопротивление проводника прохождению тока через него :

-

-

-

-

-

-

-

-

-

-

При прохождении тока через проводник свободные электроны испытывают соударения с атомами кристаллической решетки, передавая им часть своей энергии. При этом внутренняя энергия проводника увеличивается ( он нагревается и оказывает сопротивление току )

Такой вид сопротивления называется активным (есть еще один вид сопротивления – реактивное, не вызывающее нагрева проводника и обусловленное другими процессами)

Действующие значения тока и напряжения, виды сопротивлений

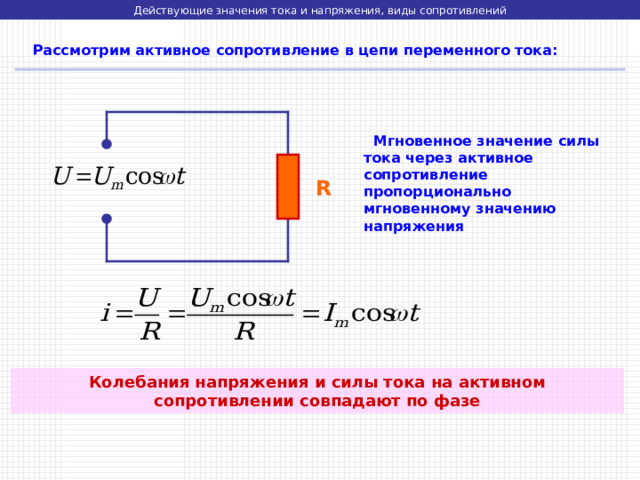
Рассмотрим активное сопротивление в цепи переменного тока:

Мгновенное значение силы тока через активное сопротивление пропорционально мгновенному значению напряжения

R

Колебания напряжения и силы тока на активном сопротивлении совпадают по фазе

Активное сопротивление в цепи переменного тока

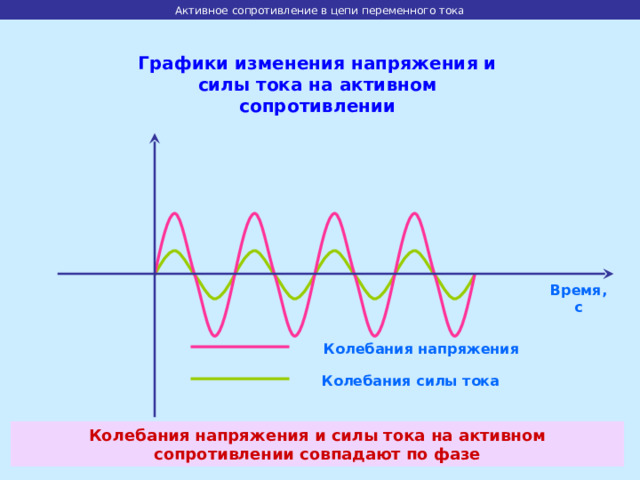
Графики изменения напряжения и силы тока на активном сопротивлении

Время, с

Колебания напряжения

Колебания силы тока

Колебания напряжения и силы тока на активном сопротивлении совпадают по фазе

Активное сопротивление в цепи переменного тока

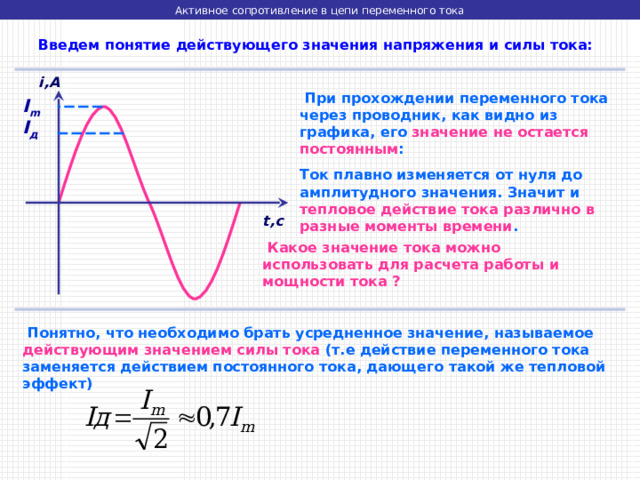
Введем понятие действующего значения напряжения и силы тока:

i,A

При прохождении переменного тока через проводник, как видно из графика, его значение не остается постоянным :

Ток плавно изменяется от нуля до амплитудного значения. Значит и тепловое действие тока различно в разные моменты времени .

I m

I д

t,c

Какое значение тока можно использовать для расчета работы и мощности тока ?

Понятно, что необходимо брать усредненное значение, называемое действующим значением силы тока (т.е действие переменного тока заменяется действием постоянного тока, дающего такой же тепловой эффект)

Активное сопротивление в цепи переменного тока

Аналогично действующее значение напряжения:

Тогда действующая мощность (средняя мощность):

а выделяемое в проводнике тепло:

2. Конденсатор в цепи переменного тока

C

Конденсатор в цепи переменного тока

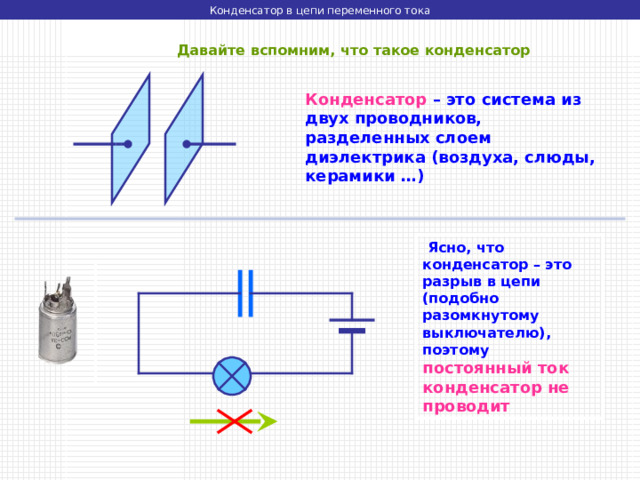
Давайте вспомним, что такое конденсатор

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика (воздуха, слюды, керамики …)

Ясно, что конденсатор – это разрыв в цепи (подобно разомкнутому выключателю), поэтому постоянный ток конденсатор не проводит

Конденсатор в цепи переменного тока

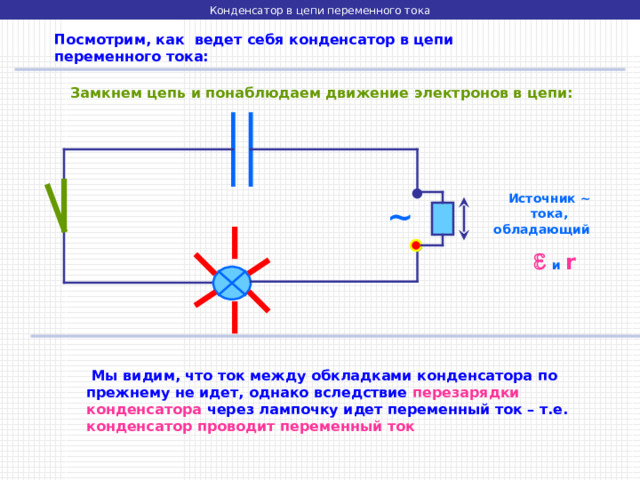
Посмотрим, как ведет себя конденсатор в цепи переменного тока:

Замкнем цепь и понаблюдаем движение электронов в цепи:

Источник ~ тока, обладающий  и r

~

Мы видим, что ток между обкладками конденсатора по прежнему не идет, однако вследствие перезарядки конденсатора через лампочку идет переменный ток – т.е. конденсатор проводит переменный ток

Конденсатор в цепи переменного тока

Итак, конденсатор проводит переменный ток, однако он оказывает току сопротивление, которое называется емкостным сопротивлением

- емкостное сопротивление

 - циклическая частота протекающего тока

С – электроемкость конденсатора

 - частота тока

Конденсатор в цепи переменного тока

Проанализируем формулу емкостного сопротивления:

Из формулы видно, что сопротивление конденсатора обратно пропорционально частоте протекающего тока и его электроемкости :

Сопротивление конденсатора уменьшается с ростом частоты, значит конденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные , а постоянный ток вообще не проводит

C 1 X С 2 С 2 Сопротивление конденсатора зависит и от его электроемкости: при фиксированной частоте конденсатор с большей емкостью будет обладать меньшим сопротивлением " width="640"

Конденсатор в цепи переменного тока

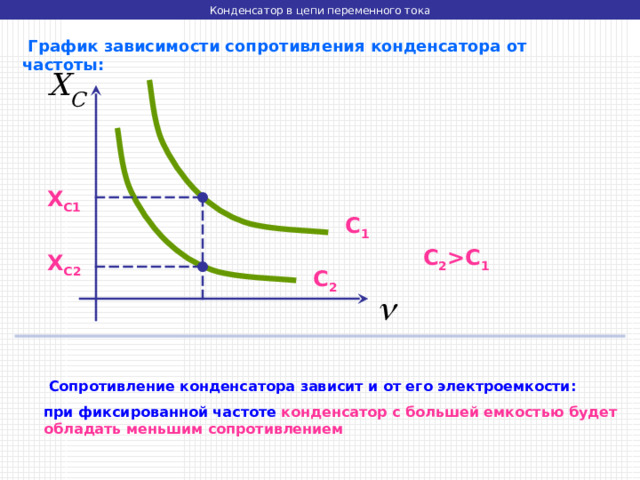
График зависимости сопротивления конденсатора от частоты:

X С1

С 1

С 2 C 1

X С 2

С 2

Сопротивление конденсатора зависит и от его электроемкости:

при фиксированной частоте конденсатор с большей емкостью будет обладать меньшим сопротивлением

Конденсатор в цепи переменного тока

Сдвиг фаз между напряжением и током:

Если напряжение на конденсаторе меняется по закону:

то заряд на конденсаторе равен:

тогда сила тока в цепи:

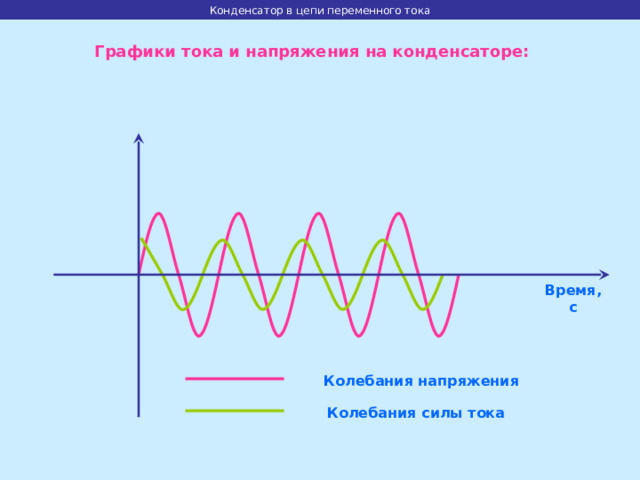
Колебания тока на конденсаторе опережают колебания напряжения на  /2

Конденсатор в цепи переменного тока

Графики тока и напряжения на конденсаторе:

Время, с

Колебания напряжения

Колебания силы тока

3. Индуктивность в цепи переменного тока

L

Индуктивность в цепи переменного тока

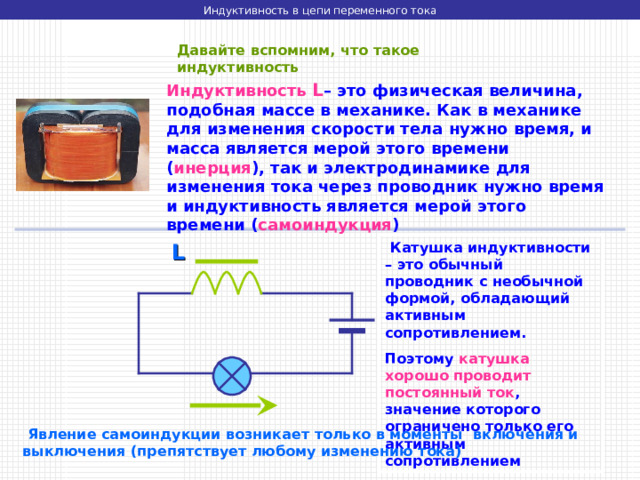
Давайте вспомним, что такое индуктивность

Индуктивность L – это физическая величина, подобная массе в механике. Как в механике для изменения скорости тела нужно время, и масса является мерой этого времени ( инерция ), так и электродинамике для изменения тока через проводник нужно время и индуктивность является мерой этого времени ( самоиндукция )

Катушка индуктивности – это обычный проводник с необычной формой, обладающий активным сопротивлением.

Поэтому катушка хорошо проводит постоянный ток , значение которого ограничено только его активным сопротивлением

L

Явление самоиндукции возникает только в моменты включения и выключения (препятствует любому изменению тока)

Индуктивность в цепи переменного тока

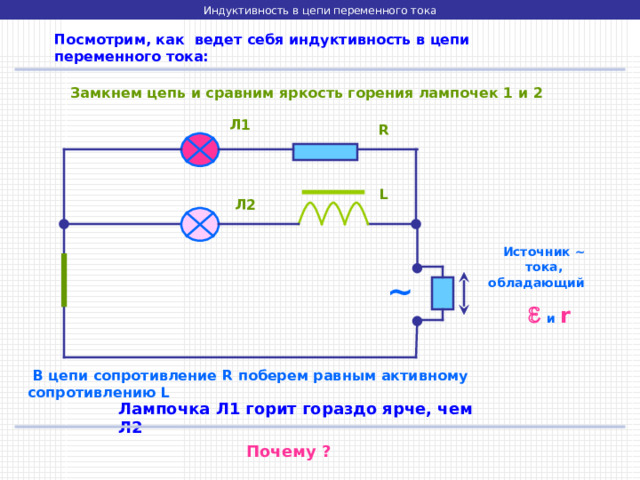
Посмотрим, как ведет себя индуктивность в цепи переменного тока:

Замкнем цепь и сравним яркость горения лампочек 1 и 2

Л1

R

L

Л2

Источник ~ тока, обладающий  и r

~

В цепи сопротивление R поберем равным активному сопротивлению L

Лампочка Л1 горит гораздо ярче, чем Л2

Почему ?

Индуктивность в цепи переменного тока

Все дело в явлении самоиндукции , возникающей в катушке при любом изменении тока, которое мешает этому изменению – поэтому у катушки индуктивности кроме активного сопротивления провода, из которого она сделана, появляется еще одно сопротивление, обусловленное явлением самоиндукции и называемое индуктивным сопротивлением X L

 - циклическая частота протекающего тока

L – индуктивность катушки

 - частота тока

Индуктивность в цепи переменного тока

Проанализируем формулу индуктивного сопротивления:

Из формулы видно, что индуктивное сопротивление прямо пропорционально частоте протекающего тока и индуктивности

Индуктивное сопротивление увеличивается с ростом частоты, значит катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные , а для постоянного тока оно равно нулю

Индуктивность в цепи переменного тока

Сдвиг фаз между напряжением и током:

Если ток в катушке изменяется по закону:

то напряжение на катушке изменяется по закону:

Ток в катушке индуктивности отстает от напряжения  /2

C I V I L

Правило:

Индуктивность в цепи переменного тока

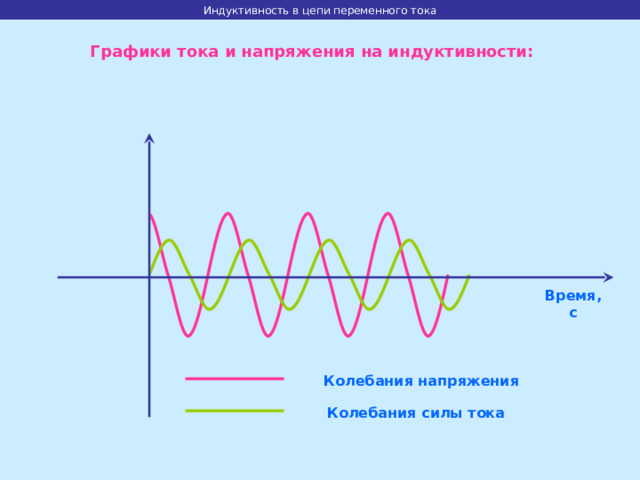
Графики тока и напряжения на индуктивности:

Время, с

Колебания напряжения

Колебания силы тока

4. Использование частотных свойств конденсатора и катушки индуктивности

5. Использование частотных свойств конденсатора и катушки

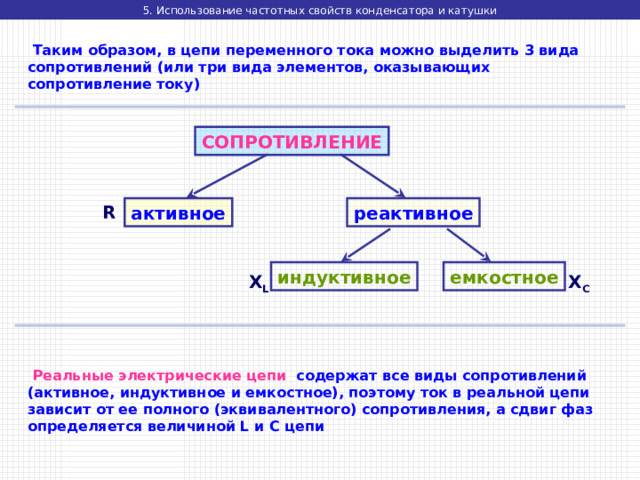
Таким образом, в цепи переменного тока можно выделить 3 вида сопротивлений (или три вида элементов, оказывающих сопротивление току)

СОПРОТИВЛЕНИЕ

R

активное

реактивное

индуктивное

емкостное

X L

X C

Реальные электрические цепи содержат все виды сопротивлений (активное, индуктивное и емкостное), поэтому ток в реальной цепи зависит от ее полного (эквивалентного) сопротивления, а сдвиг фаз определяется величиной L и C цепи

5. Использование частотных свойств конденсатора и катушки

Итак,

• конденсатор хорошо проводит ВЧ колебания, и плохо – НЧ колебания катушка наоборот: хорошо НЧ колебания и плохо – ВЧ колебания
• конденсатор хорошо проводит ВЧ колебания, и плохо – НЧ колебания катушка наоборот: хорошо НЧ колебания и плохо – ВЧ колебания
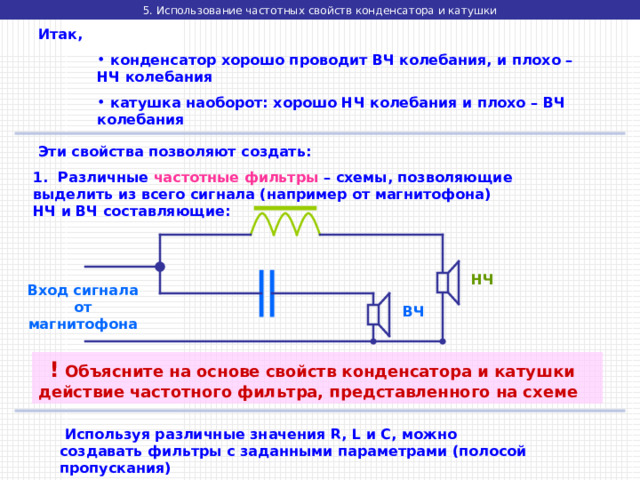
• конденсатор хорошо проводит ВЧ колебания, и плохо – НЧ колебания
• катушка наоборот: хорошо НЧ колебания и плохо – ВЧ колебания

Эти свойства позволяют создать:

1. Различные частотные фильтры – схемы, позволяющие выделить из всего сигнала (например от магнитофона) НЧ и ВЧ составляющие:

НЧ

Вход сигнала от магнитофона

ВЧ

! Объясните на основе свойств конденсатора и катушки действие частотного фильтра, представленного на схеме

Используя различные значения R, L и C , можно создавать фильтры с заданными параметрами (полосой пропускания)

5. Использование частотных свойств конденсатора и катушки

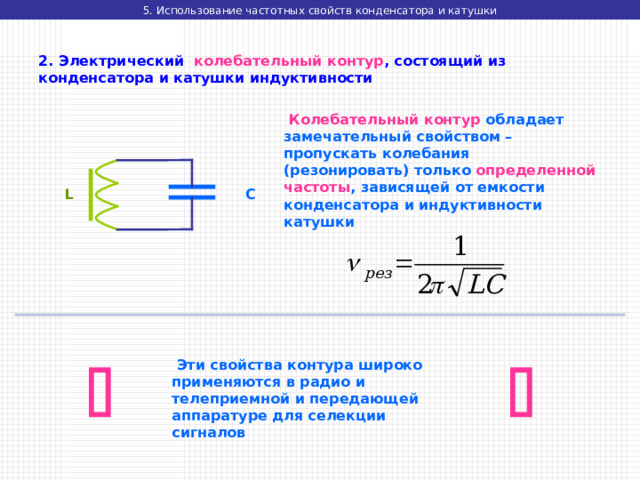
2. Электрический колебательный контур , состоящий из конденсатора и катушки индуктивности

Колебательный контур обладает замечательный свойством – пропускать колебания (резонировать) только определенной частоты , зависящей от емкости конденсатора и индуктивности катушки

L

C





Эти свойства контура широко применяются в радио и телеприемной и передающей аппаратуре для селекции сигналов

На этом урок закончен, на следующем уроке мы рассмотрим примеры решения задач на частотные свойства конденсатора и катушки индуктивности в цепи переменного тока, действующие значения электрических величин

Домнин Константин Михайлович

E – mail: [email protected]

2006 год .