Подготовка к ОГЭ 2024-
Модуль «Геометрия» (базовый уровень)
Работа учителя математики
МБОУ-СОШ №17
Г. Армавира
Краснодарского края
Ванян Риты Санасаровны
2024 уч. год
Вычисление углов.-
Параллелограмм
-
Угол А параллелограмма в 3 раза меньше угла В. Найдите угол D. (135°)
-
Сумма двух углов параллелограмма равна 110°.Найти больший угол. (125°)
-
Разность углов параллелограмма равна 80°. Найти меньший угол параллелограмма. (50°)
-
Найти меньший угол параллелограмма, если два его угла относятся как 4:5. (120°)
-
Диагональ параллелограмма образует с двумя его сторонами углы 26° и 34°. Найдите больший угол параллелограмма. (80°)
-
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне.
-
Прямоугольник
-
Диагональ прямоугольника образует с его стороной угол 58°. Найдите угол между диагоналями прямоугольника. (64°)
-
Ромб
-
Угол между диагональю ромба и его стороной равен 30°. Найдите угол между другой диагональю ромба и той же стороной. (60°)
-
Угол ромба в 2раза меньше другого угла этого ромба. Найдите меньший угол ромба. (60°)
-
Трапеция
-
Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. (70°)
-
Разность двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. (115°)
-
Один угол равнобедренной трапеции в два раза больше другого. Найдите меньший угол этой трапеции. (60°)
-
Два противолежащих угла равнобедренной трапеции относятся как 4:5. Найдите меньший угол трапеции. (80°)
-
Угол между основанием и диагональю равнобедренной трапеции равен 30°. Найдите угол между диагоналями трапеции. (60°)
-
Угол между диагоналями равнобедренной трапеции равен 76°. Найдите угол между основанием и диагональю трапеции. (38°)
-
Треугольник.
-
В равнобедренном треугольнике ABC с основанием АС величина угла АВС равна 46° . Найдите величину внешнего угла при вершине С . Ответ дайте в градусах. (113)
-
Один острый угол прямоугольного треугольника на 79° больше другого. Найти больший острый угол. Ответ дайте в градусах . (45)
-
В треугольнике ABCAC=BC. Угол C равен 116°. Найдите внешний угол CBD. Ответ дайте в градусах. (148)
-
Один их внешних углов треугольника равен 15°. Углы, не смежные с данным внешним углом, относятся как 1:4. Найдите наибольший из них. Ответ дайте в градусах. (12)
-
Один из углов равнобедренного треугольника равен 98°. Найдите один из других его углов. Ответ дайте в градусах. (41)
-
Сумма углов треугольника и внешнего угла к третьему равна 68°. Найдите этот третий угол. Ответ дайте в градусах. (146)
-
Один острый угол прямоугольного треугольника в
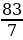 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах. (83)
раза больше другого. Найдите больший острый угол. Ответ дайте в градусах. (83) -
В треугольнике ABC угол A равен 17°, уголB равен 23°, CH- высота. Найдите разность углов ACHи BCH. Ответ дайте в градусах. (6)
-
В треугольнике ABCAD- биссектриса, угол C равен 30°, угол BAD равен 69°. Найдите угол ADB.Ответ дайте в градусах.(99)
-
В треугольнике ABCAC=BC, AD- высота, угол BAD равен 19°. Найдите угол C.Ответ дайте в градусах. (38)
-
В треугольнике ABCCD- медиана, угол ACB равен 90°, угол B равен 55°. Найдите угол ACD. Ответ дайте в градусах. (35)
-
Два угла треугольника равны 147° и 27°. Найдите тупой угол, который образует высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах. (174)
-
В треугольнике ABC CH – высота, AD – биссектриса, О – точка пересечения прямых CH и AD, угол BAD равен 74°. Найдите угол AOC. Ответ дайте в градусах. (16)
-
В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 37°. Найдите меньший угол данного треугольника. Ответ дайте в градусах. (8)
-
В треугольнике ABC уголA равен 25°, угол B равен 89°. AD, BE, CF- биссектрисы, пересекающиеся в точке О. Найдите угол AOF.Ответ дайте в градусах. (45,5)
-
В треугольнике ABC угол A равен 45°, угол B равен 45°. AD, BE, CF – высоты, пересекающиеся в точке О. Найдите угол AOF. Ответ дайте в градусах. (45)
-
В треугольнике ABCAC=BC, AB=86, высота CH равна 43
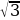 . Найдите угол C. Ответ дайте в градусах. (60)
. Найдите угол C. Ответ дайте в градусах. (60)
-
Углы в окружности.
-
Найдите центральный угол AOB, если он на 39° больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. (78)
-
Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD, AD, градусные меры которых относятся соответственно как 1:4:12:19. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах. (80)
-
Четырехугольник ABCD вписан в окружность. Угол ABC равен 48°, угол CAD равен 38°. Найдите уголABD.Ответ дайте в градусах. (10)
-
Центральный угол на 45° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах. (45)
-
Найдите вписанный угол, опирающийся на дугу, которая составляет
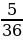 окружности.Ответ дайте в градусах. (25)
окружности.Ответ дайте в градусах. (25) -
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах. (36)
-
Дуга окружности AC, не содержащая точки B, составляет 165°. А дуга окружности BC, не содержащая точки A, составляет 55°. Найдите вписанный угол ACB.Ответ дайте в градусах. (70)
-
ACи BD – диаметры окружности с центром О. угол ACB равен 69°. Найдите угол AOD. Ответ дайте в градусах. (42)
-
Хорда ABстягивает дугу окружности в 6°. Найдите острый угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах. (3)
-
Касательные CA иCB к окружности образуют угол ACB, равный 118°. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах. (62)
-
Найдите угол ACO, если его сторона CA касается окружности, О – центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 33°. Ответ дайте в градусах. (57)
-
Найдите угол CBD, если вписанные углы ADB и ADC опираются на дуги окружности, градусные величины которых равны соответственно 128° и 48°.Ответ дайте в градусах. (40)
-
Параллелограмм
-
Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите большую сторону параллелограмма. (13)
-
Периметр параллелограмма равен 30. Одна сторона параллелограмма в два раза меньше другой. Найдите меньшую сторону параллелограмма. (50)
-
Две стороны параллелограмма относятся как 3:4, а периметр его равен 70. Найдите большую сторону параллелограмма. (20)
-
Биссектриса тупого угла параллелограмма делит противолежащую сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88. (28)
-
Прямоугольник
-
Найдите диагональ прямоугольника, если его периметр равен 28, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 24. (10)
-
Периметр прямоугольника ABCD равен 34, диагональ AC равна 13. Найдите периметр треугольника ABC. (30)
-
Меньшая сторона прямоугольника равна 6, диагонали пересекаются под углом 60°. Найдите диагональ прямоугольника. (12)
-
Ромб
-
Диагонали ромба относятся как 3:5 . Периметр ромба равен 136. Найдите высоту ромба.(15)
-
Трапеция, средняя линия трапеции
-
Найдите среднюю линию трапеции, если известно , что ее основания 111 и 112. (111,5)
-
В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60°. Найдите ее периметр. (69)
-
Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45°. Найдите высоту трапеции. (3)
-
Найдите среднюю линию трапеции, если ее основания равны 30 и 16. (23)
-
Средняя линия трапеции равна 28, а основание равно 18. Найдите другое основание трапеции. (38)
-
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию трапеции. (10)
-
Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции. (150
-
Боковые стороны трапеции равны 24 и 26,средняя линия равна 28. Найдите периметр трапеции.(106)
-
Основания трапеции относятся как 2:3, а средняя линия равна 5. Найдите меньшее основание.(4)
-
Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции. (20)
-
Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции. (9)
-
Средняя линия трапецииравна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции. (14)
-
Основания трапеции равны 6 и 4. Найдите отрезок, соединяющий середины диагоналей трапеции. (1)
-
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию. (12)
Площади фигур.
-
Квадрат.
-
Найдите площадь квадрата, если его диагональ равна 1. (0,5)
-
Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9. (6)
-
Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами 5 и 12. (13)
-
Во сколько раз увеличится площадь квадрата, если его стороны увеличится в три раза. (9)
-
Даны два квадрата, диагонали которых равны 12 и 13. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов. (5)
-
Прямоугольник.
-
Найдите площадь прямоугольника, если его периметр равен 18 и одна сторона на 3 больше другой. (18)
-
Найдите площадь прямоугольника, если его периметр равен 30, а отношение сторон равно 1:2. (50)
-
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника. (48)
-
Найдите периметр прямоугольника, если его площадь равна 16, а отношение сторон равно 1:4. (20)
-
Периметр прямоугольника равен 24, а площадь 20. Найдите большую сторону прямоугольника. (10)
-
Сторона прямоугольника относится к его диагонали как 4:5. А другая сторона равна 9. Найдите площадь прямоугольника.(108)
-
Параллелограмм.
-
Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°. (40)
-
Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону. (6)
-
Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма. (8)
-
Ромб.
-
Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°. (0,5)
-
Найдите площадь ромба, если его высота равна 2, а острый угол 30°. (8)
-
Найдите площадь ромба, если его диагонали равны 4 и 12. (24)
-
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ. (3)
-
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ. (2)
-
Треугольник.
-
Прямоугольный
-
Найдите площадь прямоугольного треугольника если его катеты равны 5 и 8. (20)
-
Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет. (8)
-
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10. (24)
-
Площадь прямоугольного треугольника равна 65. Один из его катетов на 3 больше другого. Найдите меньший катет. (10)
-
Равнобедренный
-
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника. (100)
-
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
-
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 9. (6)
-
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 100. (20)
-
Площадь равнобедренного треугольника, основание которого равно 15, а высота, опущенная на боковую сторону, равна 12. (75)
-
Произвольный
-
Найдите площадь треугольника, две стороны которого равны 11 и 14, а угол между ними 30°. (77)
-
Площадь треугольника равна 12. Две его стороны равны 6 и 8. Найдите угол между этими сторонами. (30° или 150°)
-
Периметр треугольника равен 8, а радиус вписанной окружности равен 2. Найдите площадь этого треугольника. (8)
-
Площадь треугольника равна 205, а его периметр 82. Найдите радиус вписанной окружности. (5)
-
Трапеция.
-
Основания трапеции равны 1 и 3, высота 1. Найдите площадь трапеции. (2)
-
Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции. (6)
-
Основания трапеции 8 и 34, площадь равна 168. Найдите его высоту. (8)
-
Основание трапеции равно 13, высота 5, а площадь равна 50. Найдите второе основание трапеции. (7)
-
Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции. (15)
-
Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции. (8)
-
Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции. (160)
-
Основания равнобедренной трапеции равны 7 и 13. А ее площадь равна 40. Найдите периметр трапеции. (30)
-
Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием 45°. (16)
-
Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. (45°)
-
Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции. (42)
-
Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. (30)
-
Круг.
-
Площадь круга равна
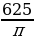 . Найдите длину его окружности. (50)
. Найдите длину его окружности. (50) -
Найдите площадь сектора круга радиуса
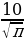 , центральный угол которого равен 90°. (25)
, центральный угол которого равен 90°. (25) -
Найдите площадь сектора круга радиуса 24, длина дуги которого равна 3. (36)
-
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны
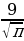 и
и 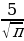 . (56)
. (56) -
Найдите центральный угол сектора круга радиуса
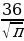 , площадь которого 216. Ответ дай те в градусах. (60)
, площадь которого 216. Ответ дай те в градусах. (60) -
Площадь сектора круга радиуса 22 равна 165. Найдите длину его дуги. (15)
-
Многоугольник.
-
Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника. (50)
-
Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр. (22)
-
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь. (30)
-
Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.(1)
-
Диагонали четырехугольника перпендикулярны и равны 4 и 6. Найдите площадь этого четырехугольника. (12)
-
Диагонали четырехугольника образуют угол 30°и равны 4 и 6.Найдите площадь этого четырехугольника. (6)
Тригонометрия.
-
В треугольнике ABC угол C равен 90°, sinA=
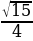 . Найдите cosA. (0,25)
. Найдите cosA. (0,25) -
В треугольнике ABC угол C равен 90°, cosA=
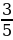 . Найти cos B. (0,8)
. Найти cos B. (0,8) -
В треугольнике ABC угол C равен 90°, cosA=
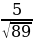 . Найдите tg A. (1,6)
. Найдите tg A. (1,6) -
В треугольнике ABC угол C равен 90°,tgA=2
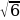 . Найти cos A. (0,2)
. Найти cos A. (0,2) -
В треугольнике ABC угол C равен 90°,tgA=
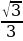 .Найти sin A. (0,5)
.Найти sin A. (0,5) -
В треугольнике ABC угол C равен 90°,AB=10, sinA=0,9. Найти BC. (9)
-
В треугольнике ABC угол C равен 90°,AB=16, cosA=0,25. Найти AC. (4)
-
В треугольнике ABC угол C равен 90°,AB=39, cosB=
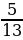 . Найти AC. (36)
. Найти AC. (36) -
В треугольнике ABC угол C равен 90°,CH – высота, AB=16, sinA=
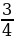 . Найдите BH. (9)
. Найдите BH. (9) -
В треугольнике ABC угол C равен 90°,cosA=0,5.Найдите CH. (12)
-
В треугольнике ABCAC=BC, AB=8,cosA=0,2. Найти AC. (20)
-
В треугольнике ABCAC=BC=30, tgA=
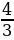 . Найти AB. (18)
. Найти AB. (18) -
В треугольнике ABCAC=BC=14, AB=14. Найти cos A. (0,5)
-
В треугольнике ABCAC=BC=15, AB=6
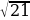 . Найти sin A.(0,4)
. Найти sin A.(0,4) -
В треугольнике ABCAC=BC=10, AB=16. Найти tg A. (0,75)
Основные понятия и утверждения геометрии.
Для каждого из следующих утверждений укажите, верно оно или нет.
-
Прямые
-
Любые две прямые имеют ровно одну общую точку. (нет)
-
Если две прямые перпендикулярны третьей прямой, то эти две прямые перпендикулярны. (нет)
-
Любые две прямые имеют не менее одной общей точки. (нет)
-
Через любые две точки проходит не менее одной прямой. (да)
-
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны. (да)
-
Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны. (да)
-
Если расстояние от точки до прямой меньше 7, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 7. (нет)
-
Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны. (нет)
-
Углы
-
Вертикальные углы равны. (да)
-
Сумма вертикальных углов равна 180°. (нет)
-
Сумма двух смежных углов 180°. (да)
-
Смежные углы равны. (нет)
-
Если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы равны. (нет)
-
Если вписанный угол равен 60°, то центральный угол, опирающийся на ту же дугу окружности, равен 120°. (да)
-
Если вписанный угол равен 60°, то центральный угол, опирающийся на ту же дугу окружности, равен 30°. (нет)
-
Если угол равен 30°, то вертикальный ему угол равен 150°. (нет)
-
Если дуга окружности составляет 80°, то центральный угол, опирающийся на эту дугу, равен 40°. (нет)
-
Треугольники
-
Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны. (нет)
-
Если две стороны и угол между ними одного треугольника соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (да)
-
Если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны. (да)
-
Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники равны. (нет)
-
Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники подобны. (да)
-
Если гипотенуза одного прямоугольного треугольника равна гипотенузе другого прямоугольного треугольника, то такие треугольники равны. (нет)
-
Каждая сторона треугольника равна сумме двух других сторон. (нет)
-
Каждая сторона треугольника больше суммы двух других сторон. (нет)
-
Каждая сторона треугольника меньше разности двух других сторон. (нет)
-
Сумма углов треугольника равна 180°. (да)
-
Сумма углов прямоугольного треугольника равна 180°. (да)
-
В треугольнике против меньшего угла лежит большая сторона. (нет)
-
В треугольнике против меньшей стороны лежит меньший угол. (да)
-
Любые два равносторонних треугольника равны. (да)
-
Любые два равнобедренных треугольника равны. (нет)
-
Любые два прямоугольных треугольника равны. (нет)
-
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними. (нет)
-
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.(да)
-
Треугольник ABC, у которого AB=3, BC=4, AC=5, является тупоугольным. (нет)
-
Треугольник ABC, у которого AB=4, BC=5, AC=6, является прямоугольным. (нет)
-
Площадь треугольника равна произведению его стороны на высоту, проведенную к этой стороне. (нет)
-
Площадь треугольника равна половине произведения стороны на высоту. (нет)
-
Площадь прямоугольного треугольника равна произведению его катетов. (нет)
-
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. (да)
-
В прямоугольном треугольнике все углы прямые. (нет)
-
Треугольник со сторонами 1, 2, 4 не существует. (да)
-
В тупоугольном треугольнике сумма углов больше 180°. (нет)
-
Любые два равнобедренных прямоугольных треугольника подобны. (да)
-
Стороны треугольника пропорциональны градусным величинам противолежащих углов. (нет)
-
В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета. (да)
-
Площадь прямоугольного треугольника равна удвоенному произведению его катетов. (нет)
-
В Треугольнике ABC, для которого AB=4, BC=5, AC=6, угол A наибольший. (нет)
-
Внешний угол треугольника больше каждого не смежного с ним внутреннего угла. (да)
-
Четырехугольники
-
Сумма углов выпуклого четырехугольника равна 180°. (нет)
-
Сумма углов выпуклого четырехугольника равна 360°. (да)
-
Сумма противоположных углов четырехугольника равна 180°. (нет)
-
Сумма противоположных углов параллелограмма равна 180°. (нет)
-
Если в четырехугольнике две стороны параллельны, то этот четырехугольник- параллелограмм. (нет)
-
Если в четырехугольнике два угла – прямые, то этот четырехугольник – параллелограмм. (нет)
-
Если в четырехугольнике три угла – прямые, то этот четырехугольник – параллелограмм. (да)
-
Диагонали параллелограмма делят его углы пополам. (нет)
-
Диагонали параллелограмма перпендикулярны. (нет)
-
Диагонали ромба точкой пересечения делятся пополам. (да)
-
Диагонали квадрата равны. (да)
-
Площадь прямоугольника равна произведению двух его сторон. (нет)
-
Площадь прямоугольника равна произведению двух его смежных сторон. (да)
-
Площадь ромба равна произведению его стороны на высоту, проведенную к этой стороне. (да)
-
Площадь трапеции равна произведению суммы оснований на высоту. (нет)
-
Сумма углов ромба равна 360°. (да)
-
Сумма двух противоположных углов равнобедренной трапеции равна 180°. (да)
-
Диагонали параллелограмма параллельны. (нет)
-
Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат. (да)
-
Если диагонали ромба равны 3 и 4. То его площадь равна 6. (да)
-
Площадь трапеции равна произведению средней линии на высоту. (да)
-
Окружность
-
Длина окружности радиуса R равна πR. (нет)
-
Длина окружности радиуса R равна 2πR. (да)
-
Если расстояние от точки до центра окружности меньше или равно радиусу окружности, то эта точка лежит на окружности. (нет)
-
Если расстояние от центра окружности до прямой меньше диаметра окружности, то эти прямая и окружность пересекаются. (нет)
-
Площадь круга равна квадрату его радиуса. (нет)
-
Через любые три точки проходит единственная окружность. (нет)
-
Если расстояние от центра окружности до прямой меньше радиуса окружности, то эти прямая и окружность пересекаются. (да)
-
Если расстояние между центрами двух окружностей меньше суммы радиусов, то эти окружности пересекаются. (нет)
-
Площадь круга радиусаR равна 2πR. (нет)
-
Центром окружности, описанной около правильного треугольника, является точка пересечения высот. (да)
-
В любой четырехугольник можно вписать не более одной окружности. (да)
-
Если стороны прямоугольника равны 3 и 4, то диаметр описанной около него окружности равен 5. (да)
13)В любой четырехугольник можно вписать окружность(нет)
Список литературы
-
Учебник «Геометрия 7-9» под редакцией Л.С.Атанасяна , В.Ф Бутузова, С.Б. Кадомцева и др. , Просвещение ,2020 г.
-
Сборник Типовые экзаменационные варианты ОГЭ 2024., под редакцией И.В.Ященко,
-
Сайт ФИПИ
-
Сайт МИОО.
Вычисление углов. 2
Вычисление длин. 3
Площади фигур. 4
Тригонометрия. 8

 Получите свидетельство
Получите свидетельство Вход
Вход












 Дидактические материалы по геометрии "Подготовка к ОГЭ" (44.66 KB)
Дидактические материалы по геометрии "Подготовка к ОГЭ" (44.66 KB)
 0
0 106
106 2
2 Нравится
0
Нравится
0


