Диагностический контроль материала по темам " Тригонометрические формулы. Производная и её геометрический смысл"

Диагностический контроль материала

по темам « Тригонометрические функции. Производная и её геометрический смысл» для 11 класса.

Составила: учитель математики МБОУ «Нововерхиссенская СОШ» Тувышкина Надежда Сергеевна.

[email protected]

1. Найти область определения функции:

а) y= cos3x; б) y=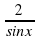 ; в) y= tg 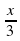; г) y= ;

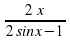2. Найти множество значений функции:

а) y= 2+cosx; б) 1+ 3sin4x;

3. Выяснить, является ли данная функция чётной или нечётной:

а) y=x cosx; б) y= ;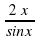

4. Найти все корни уравнения, принадлежащие отрезку :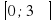

а) cosx= - -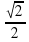 ; б) sinx= ;

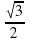5. Найти производные функций:

а) x¹²; б) 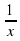; в) (2x + 7)²; г) 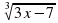; д) ( 7x -3)^-3; е) 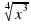; ж) 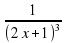; з) 3x² + 6x+ 3;

6. Найти мгновенную скорость тела, движущегося по закону s(t) = 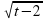, в момент времени

t= 2.

7. Найти значения х , при которых значение производной функции f(x) больше 0, равно 0, меньше 0: f(x) = 2x³+x²-4x+1.

8. Найти угловой коэффициент касательной к графику функции y= f(x) в точке с абсциссой х₀:

f(x)=x⁴, x₀=2.

9. Найти угол между касательной к графику функции y= f(x) в точке с абсциссой x₀ и осью Ох:

f(x)= 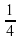x⁴, x₀ = 1.

10. Написать уравнение касательной к графику функции y= f(x) в точке с абсциссой х₀:

f(x)= x³+ 4x²-2x , x₀= 2.