Четыре замечательные точки треугольника

Четыре замечательные точки треугольника

Геометрия 8 класс

Выполнила: Василик Татьяна Тимофеевна, учитель математики МОУ ЦО «Открытие», г. Комсомольска-на-Амуре, Хабаровского края

Решите задачи:

А

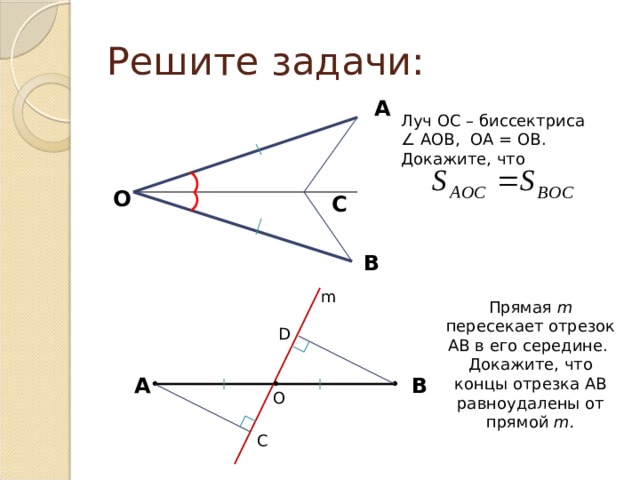
Луч ОС – биссектриса ∠ АОВ, ОА = ОВ. Докажите, что

О

С

В

m

Прямая m пересекает отрезок АВ в его середине.

Докажите, что концы отрезка АВ равноудалены от прямой m .

D

А

В

•

•

•

O

C

Теорема:

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Доказательство:

1) Пусть М- произвольная точка биссектрисы ∠ВАС, проведем перпендикуляры МК и ML. Рассмотрим ∆АМК и ∆AML. Они равны по гипотенузе и острому углу (АМ –общая гипотенуза, ∠1= ∠2 по условию). ⇒ МК = МL.

В

К

M

1

•

А

2

2) Пусть точка М лежит внутри ∠ВАС . Проведем перпендикуляры МК и МL к прямым АВ и АС. Прямоугольные треугольники АКМ и АLМ равны по гипотенузе и катету ( АМ – общая гипотенуза, МК = МL по условию). ⇒ ∠1 = ∠2. Значит луч АМ – биссектриса ∠ВАС.

L

С

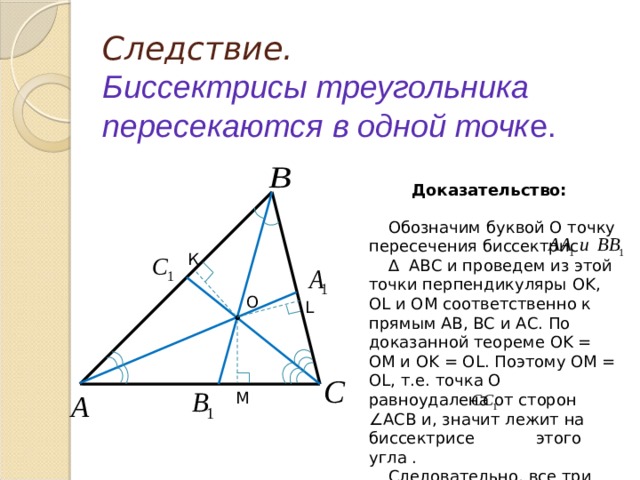
Следствие. Биссектрисы треугольника пересекаются в одной точк е.

Доказательство:

Обозначим буквой О точку пересечения биссектрис

∆ АВС и проведем из этой точки перпендикуляры OK , OL и OM соответственно к прямым АВ, ВС и АС. По доказанной теореме OK = OM и OK = OL . Поэтому OM = OL , т.е. точка О равноудалена от сторон ∠АСВ и, значит лежит на биссектрисе этого угла .

Следовательно, все три биссектрисы ∆ АВС пересекаются в точке О.

К

O

L

•

М

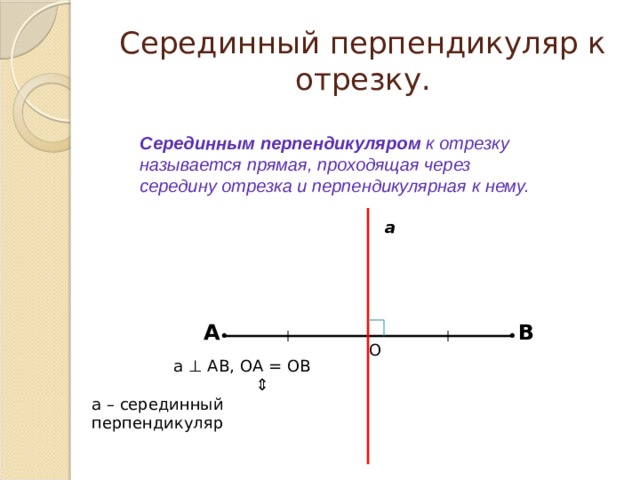
Серединный перпендикуляр к отрезку.

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему.

а

А

В

•

•

О

а ⊥ АВ, ОА = ОВ

⇕

а – серединный перпендикуляр

Теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратно : каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство:

М

•

• Пусть прямая m – серединный перпендикуляр к отрезку АВ. Рассмотрим произвольную точку М прямой m . Проведем отрезки АМ и ВМ. Прямоугольные треугольники АОМ и ВОМ равны по двум катетам ( ОА = ОВ по условию, ОМ – общий катет) ⇒ АМ = ВМ

•

•

О

А

В

m

m

2) Так как AN = NB , то ∆ABN равнобедренный.

NO – медиана этого треугольника ⇒NO – высота этого треугольника. Таким образом, NO ⊥ AB, поэтому прямые ON и m совпадают, значит N – точка прямой m.

О

А

В

•

•

•

N

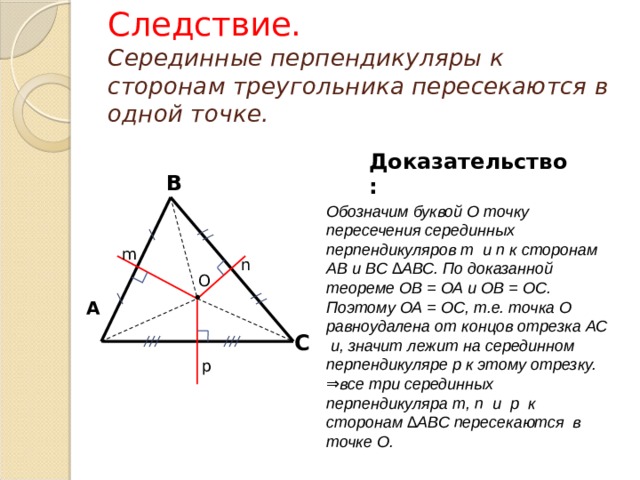
Следствие. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство:

В

Обозначим буквой О точку пересечения серединных перпендикуляров m и n к сторонам АВ и ВС ∆АВС. По доказанной теореме ОВ = ОА и ОВ = ОС. Поэтому ОА = ОС, т.е. точка О равноудалена от концов отрезка АС и, значит лежит на серединном перпендикуляре p к этому отрезку. ⇒все три серединных перпендикуляра m, n и p к сторонам ∆АВС пересекаются в точке О.

m

n

О

•

А

С

p

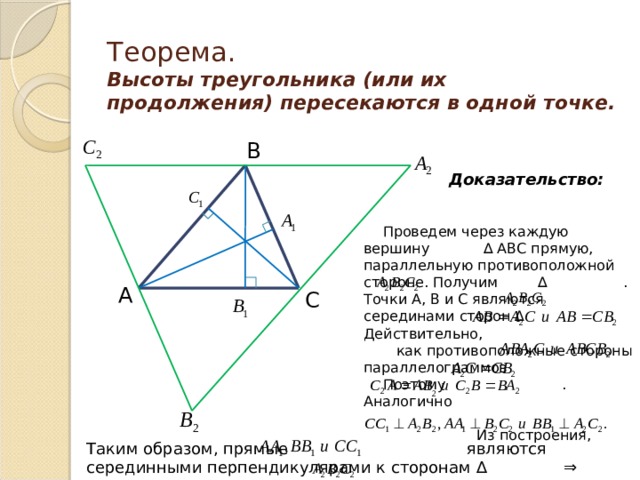
Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке.

В

Доказательство:

Проведем через каждую вершину ∆ АВС прямую, параллельную противоположной стороне. Получим ∆ . Точки А, В и С являются серединами сторон ∆ . Действительно,

как противоположные стороны параллелограммов

Поэтому . Аналогично

Из построения,

А

С

Таким образом, прямые являются серединными перпендикулярами к сторонам ∆ ⇒ пересекаются в одной точке.