Четырёхугольники

Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

Ромбом называется параллелограмм, у которого все стороны равны.

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.

Квадратом называется прямоугольник, у которого все стороны равны.

Прямоугольником называется параллелограмм, у которого все углы прямые.

• «Четырехугольники»

• Работу выполнила
• учениц а 9 класса
• Боярко Яна
• учитель: Лата С.В.

КРОССВОРД

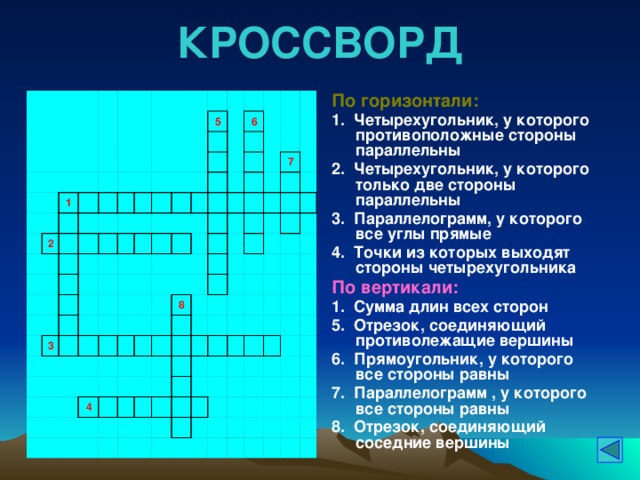
По горизонтали:

1. Четырехугольник, у которого противоположные стороны параллельны

2. Четырехугольник, у которого только две стороны параллельны

3. Параллелограмм, у которого все углы прямые

4. Точки из которых выходят стороны четырехугольника

По вертикали:

1. Сумма длин всех сторон

5. Отрезок, соединяющий противолежащие вершины

6. Прямоугольник, у которого все стороны равны

7. Параллелограмм , у которого все стороны равны

8. Отрезок, соединяющий соседние вершины

1

2

5

3

6

7

8

4

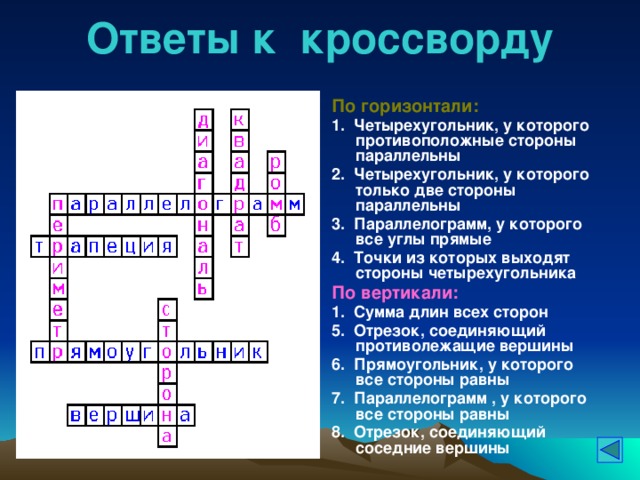
Ответы к кроссворду

По горизонтали:

1. Четырехугольник, у которого противоположные стороны параллельны

2. Четырехугольник, у которого только две стороны параллельны

3. Параллелограмм, у которого все углы прямые

4. Точки из которых выходят стороны четырехугольника

По вертикали:

1. Сумма длин всех сторон

5. Отрезок, соединяющий противолежащие вершины

6. Прямоугольник, у которого все стороны равны

7. Параллелограмм , у которого все стороны равны

8. Отрезок, соединяющий соседние вершины

Четырехугольники:

параллелограмм

трапеция

ромб

прямоугольник

квадрат

другие четырехугольники

Параллелограмм

• Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

Ромб

• Ромбом называется параллелограмм, у которого все стороны равны.

Трапеция

• Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.

Квадрат

• Квадратом называется прямоугольник, у которого все стороны равны.

Прямоугольник

• Прямоугольником называется параллелограмм, у которого все углы прямые.

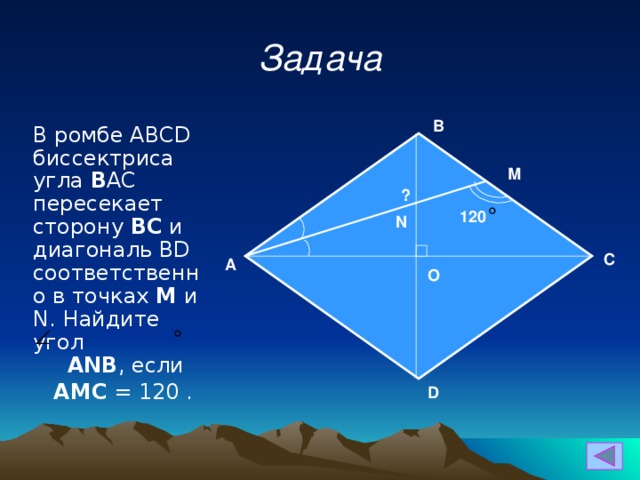
Задача

B

В ромбе ABCD биссектриса угла В AC пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите угол АNВ , если

АМС = 120 .

М

?

120

N

C

A

О

D

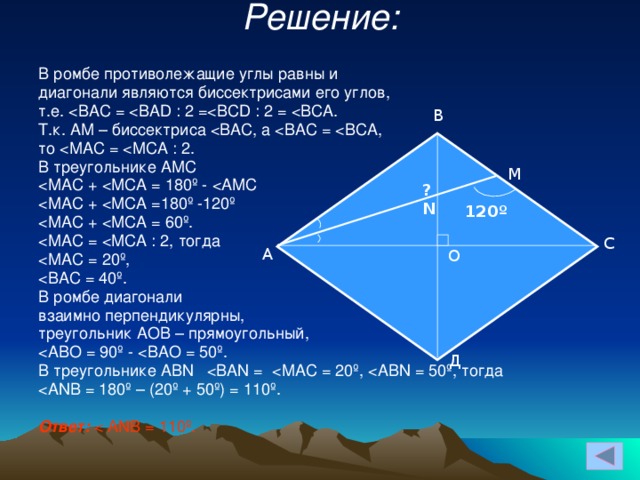
Решение:

В ромбе противолежащие углы равны и

диагонали являются биссектрисами его углов,

т.е.

Т.к. АМ – биссектриса

то

В треугольнике АМС

В ромбе диагонали

взаимно перпендикулярны,

треугольник АОВ – прямоугольный,

В треугольнике АВN

Ответ:

В

М

?

N

120 º

С

А

О

Д

спасибо

всем за внимание