“Учиться можно только весело…
Чтобы переваривать знания, надо поглощать их с аппетитом”.
Французский писатель XIX столетия Анатоль Франс.
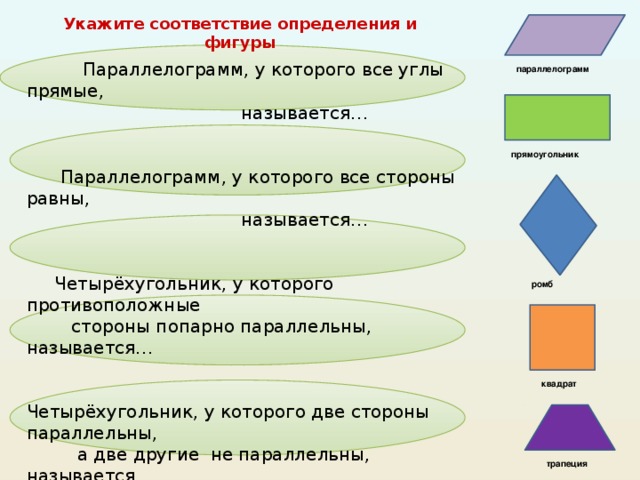
Укажите соответствие определения и фигуры.
Параллелограмм, у которого все углы прямые, называется…
Параллелограмм, у которого все стороны равны, называется…
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется…
Четырёхугольник, у которого две стороны параллельны, а две другие не параллельны, называется…
Прямоугольник, у которого все стороны равны, называется…

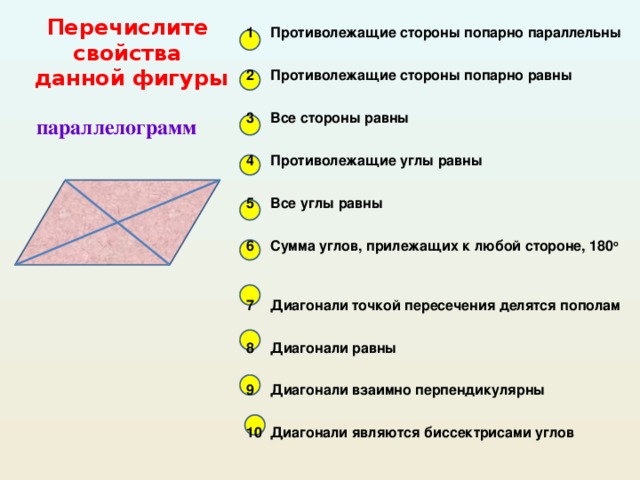
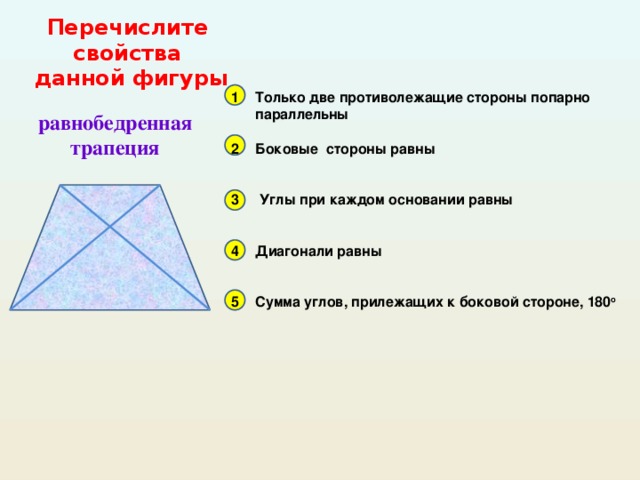
Перечислите свойства данной фигуры - параллелограмм.
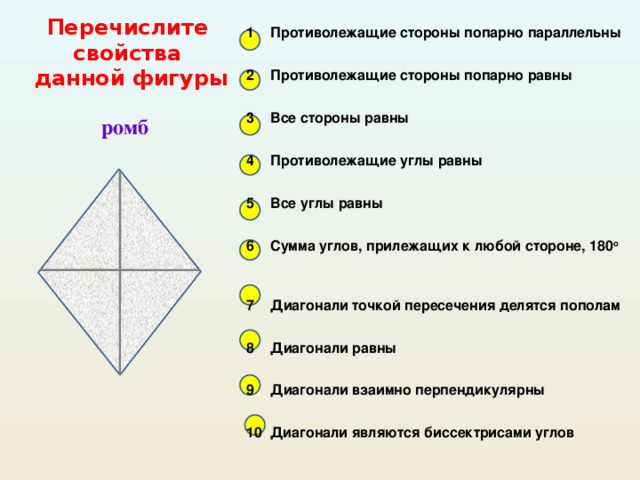
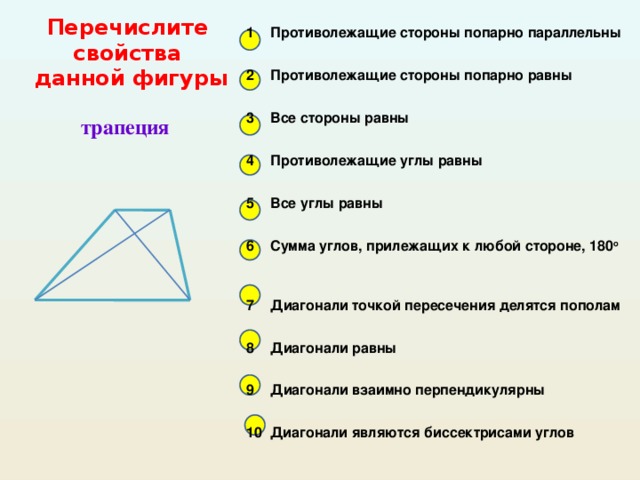
1. Противолежащие стороны попарно параллельны.
2. Противолежащие стороны попарно равны.
3. Все стороны равны.
4. Противолежащие углы равны.
5. Все углы равны.
6. Сумма углов, прилежащих к любой стороне, 180.
7. Диагонали точкой пересечения делятся пополам.
8. Диагонали равны.
9. Диагонали взаимно перпендикулярны.
10. Диагонали являются биссектрисами углов.
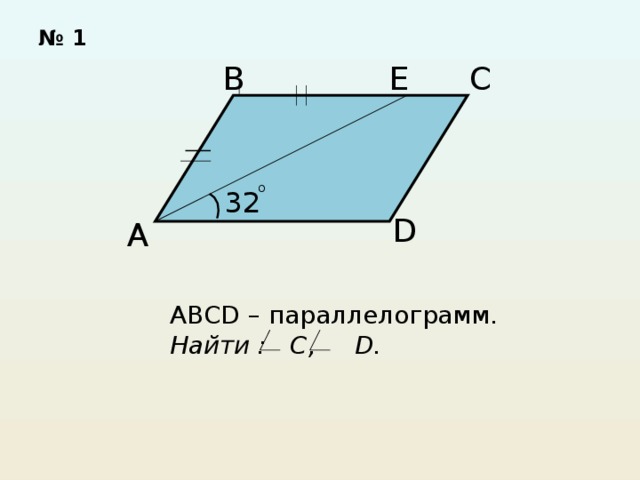
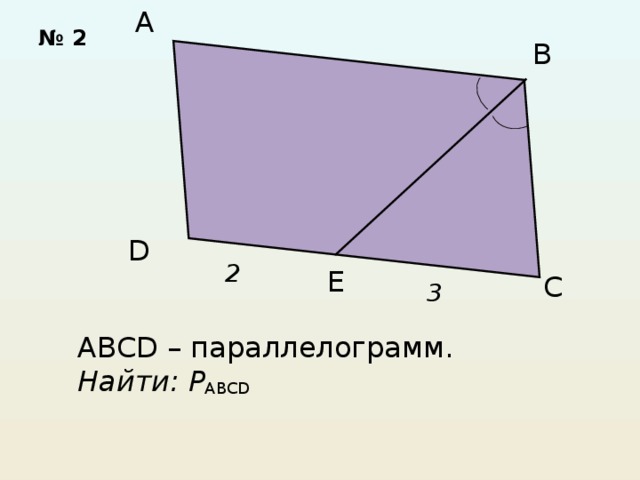
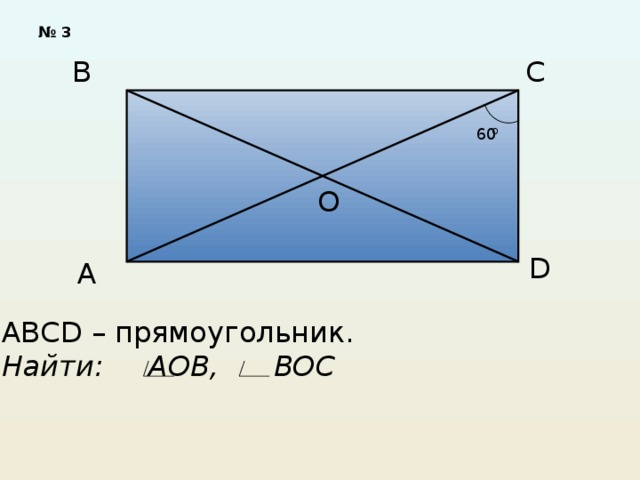
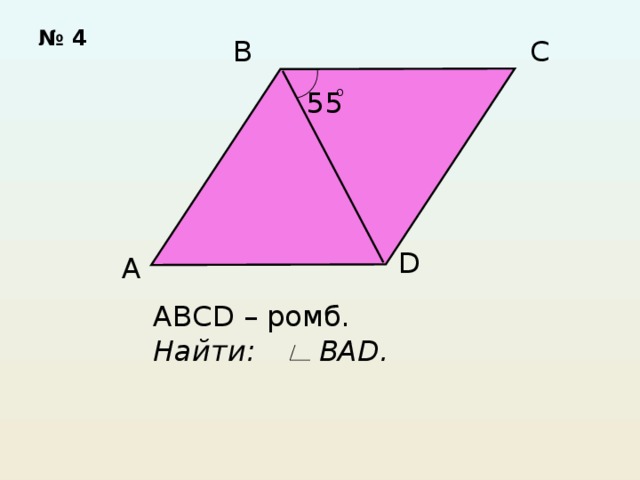
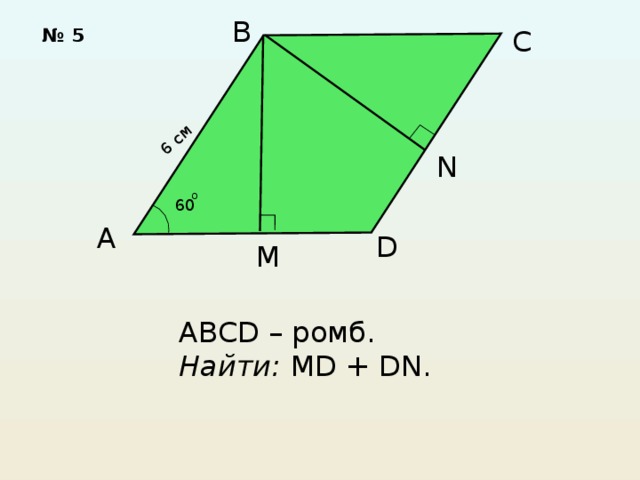
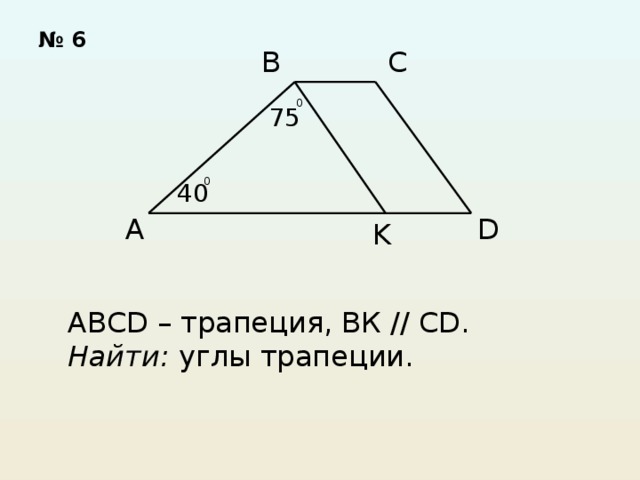
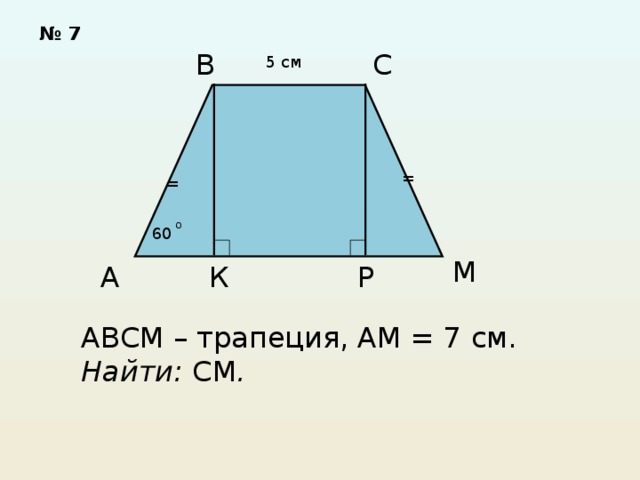
Решите задачи по готовым рисункам.

 Получите свидетельство
Получите свидетельство Вход
Вход















 Четырёхугольники (0.12 MB)
Четырёхугольники (0.12 MB)
 0
0 1293
1293 23
23 Нравится
0
Нравится
0






