Рациональные числа

Числа появились в практической деятельности для подсчета количества предметов. Такие числа, кроме нуля, называют натуральными числами. Они образуют множество натуральных чисел.

От первой буквы латинского слова naturalis – естественный, природный.

Если к натуральным числам присоединить число нуль и противоположные им числа (т.е. целые отрицательные числа), то получится множество целых чисел.

От первой буквы немецкого слова zahl – число.

А если к множеству целых чисел присоединить все дробные числа (положительные и отрицательные), то получится множество рациональных чисел.

От первой буквы французского слова quotient – отношение.

Для того чтобы записать, что какое-либо число принадлежит рассматриваемому множеству, используют вот такой знак принадлежности .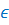

Введённые обозначения множеств чисел и знак принадлежности позволяют кратко записывать утверждения.

Например:

«Число 5 принадлежит множеству натуральных чисел»

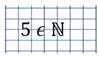
«Число –51 принадлежит множеству целых чисел»

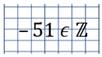
«Число −5/7 является рациональным числом»

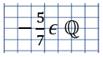
Число не принадлежит множеству:

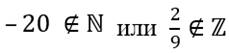
Теперь рассмотрим, понятие подмножества.

Пусть есть некоторые два множества А и В.

Пусть каждый элемент множества В является элементом множества А.

В таких случаях, говорят, что множество В является подмножеством множества А.

Для записи этого утверждения также есть определенный знак 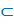, называют его знаком включения (т.е. одно множество содержится в другом).

Записывают это утверждение так:

а читают: В – подмножество множества А.

Понятие разности множеств.

Разностью множеств А и В называется множество, состоящее из всех элементов, которые принадлежат множеству А и не принадлежат множеству В.

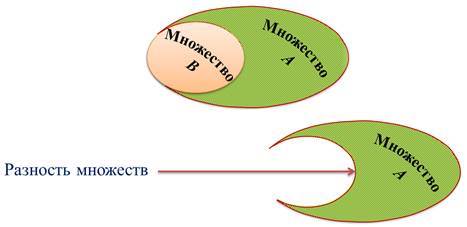
Например, разность множества целых чисел и множества натуральных чисел является множество, состоящее из всех целых отрицательных чисел и нуля.

Вернёмся к рациональным числам. Вы уже знаете, что любое рациональное число, как целое, так и дробное, можно представить в виде дроби , где m – целое число, n – натуральное. Одно и то же рациональное число можно представить в таком виде разными способами.

Например:

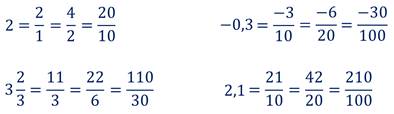
Сумма, разность и произведение рациональных чисел, тоже рациональные числа. Например:

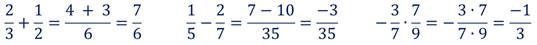
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.

Например:

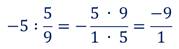
Обыкновенную дробь можно перевести в десятичную.

Например:

Бесконечные десятичные дроби такого вида называют периодическими. В периодических дробях повторяется одна или несколько цифр. Повторяющиеся цифры называют периодом. При записи периодических десятичных дробей период пишут один раз, заключая его в круглые скобки: читают эту запись так «нуль целых и 63 в периоде».

Например:

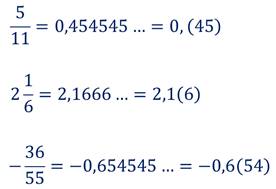
Замечание: любое рациональное число можно записать не только в виде обыкновенной дроби, но и в виде десятичной (конечной десятичной дроби), либо в виде бесконечной десятичной периодической дроби.

Любое целое число и любую конечную десятичную дробь можно записать в виде бесконечной десятичной периодической дроби. Для этого нужно приписать справа в качестве десятичных знаков бесконечную последовательность нулей.

Например:

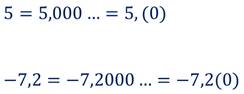
Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби.

Верно и обратное утверждение: любая бесконечная десятичная периодическая дробь есть рациональное число.

Итоги:

Любое рациональное число, как целое, так и дробное, можно представить в виде дроби , где m – целое число, n – натуральное.

Сумма, разность и произведение рациональных чисел, тоже рациональные числа.

Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.

Любое рациональное число можно записать не только в виде обыкновенной дроби, но и в виде десятичной (конечной десятичной дроби), либо в виде бесконечной десятичной периодической дроби.

Любая бесконечная десятичная периодическая дробь есть рациональное число.