Давайте рассмотрим пример:
Пусть расстояние в 200 км автомобиль со скоростью равной v км/ч преодолеет за время равное t часов. Тогда используя формулу пути, зависимость времени от скорости движения автомобиля при равном расстоянии можно выразить формулой:

Напомню, что такую зависимость называют обратно пропорциональной. Т.к. при увеличении одной величины вторая величина будет уменьшаться.
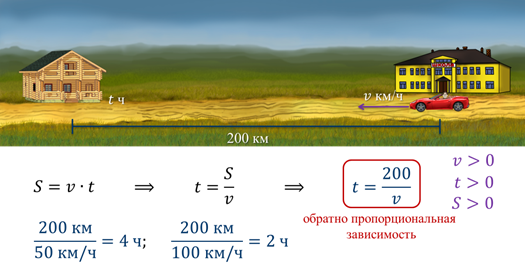
Вот, например, если автомобиль будет ехать со скоростью 50 км/ч, то на преодоление расстояния в 200 км ему понадобится 4 часа.
А вот, если автомобиль будет ехать со скоростью 100 км/ч, то на преодоление этого же пути, ему понадобится всего лишь 2 часа. Видим, что при увеличении скорости, времени тратится меньше.
Но в этой задаче переменные v и t могут принимать лишь положительные значения, т.к. скорость, время и расстояние это положительные величины.
В дальнейшем мы будем рассматривать функции, задаваемые формулой вида:

Такие функции называют обратными пропорциональностями.
С обратной пропорциональностью мы с вами часто встречаемся в повседневной жизни.
Например:
Масса m кг конфет, которую можно купить на 1 000 рублей по цене p рублей за кг. Зависимость массы конфет от стоимости за килограмм является обратно пропорциональной. Или, если есть прямоугольник длина которого a см, а ширина b см с площадью равной 27 см2. Такая зависимость также является обратно пропорциональной.

Определение:
Обратной пропорциональностью называется функция, которую можно задать формулой вида:

где x – независимая переменная и k – не равное 0 число.
Число k – называют коэффициентом обратной пропорциональности.
В нашем примере

Областью определения функции, заданной формулой вида:

является множество действительных чисел,
отличных от нуля, т.к. выражение  имеет смысл при любых x, кроме x равное нулю.
имеет смысл при любых x, кроме x равное нулю.
Теперь давайте построим график обратной
пропорциональности  .
.
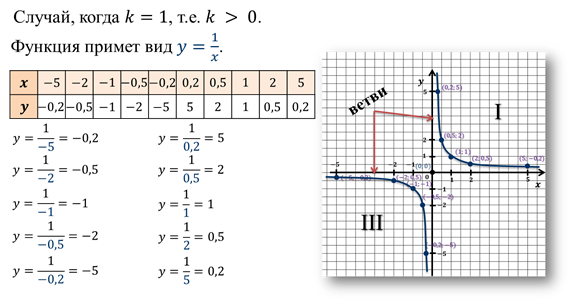
Полученный график состоит из двух симметричных относительно начала координат частей. Их обычно называют ветвями. Одна из этих ветвей расположена в первой четверти, вторая – в третьей.
График функции  при
любом k > 0 имеет такой же вид, что и график
функции
при
любом k > 0 имеет такой же вид, что и график
функции  .
.
Теперь построим график функции  .
.
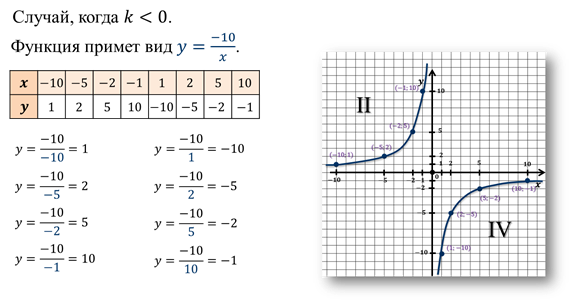
Такой же вид
имеет график функции  при
любом k < 0.
при
любом k < 0.
Определение:
Кривую, являющуюся графиком обратной пропорциональности, называют гиперболой.
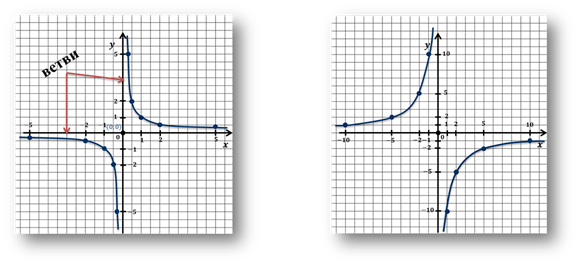
Гипербола состоит из двух ветвей.
Задание: задайте формулой обратную пропорциональность, зная, что её график проходит через точку А с координатами (10; 0,5). Постройте указанную гиперболу.
Решение:
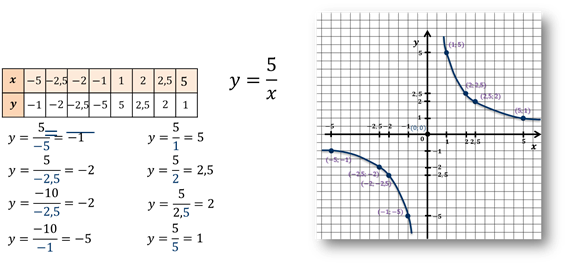
Задание: функция задана формулой  .
Заполните таблицу.
.
Заполните таблицу.
Решение:
Для того чтобы заполнить таблицу, надо подставлять известные данные в формулу функции и решать полученные уравнения.

Итоги:
Обратной пропорциональностью называется функция, которую можно задать формулой вида:

где x – независимая переменная и k – не равное 0 число.
Число k – называют коэффициентом обратной пропорциональности.
Кривую, являющуюся графиком обратной пропорциональности, называют гиперболой.
Гипербола состоит из двух ветвей. При k > 0 ветви гиперболы лежат в 1-ой и 3-ей четвертях. При k < 0 ветви гиперболы лежат во 2-ой и 4-ой четвертях.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 11413
11413

