Любое числовое выражение после выполнения всех входящих в его состав арифметических действий принимает конкретное числовое значение. Точно также состоит дело и с рациональными выражениями. Любое рациональное выражение после выполнения преобразований принимает вид рациональной дроби. Для этого рациональные выражения предварительно преобразуют или упрощают.
Числовое выражение:
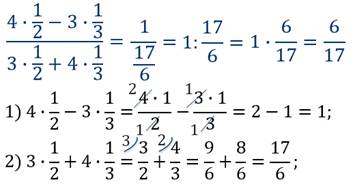
Рациональное выражение:
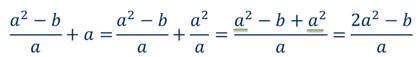
Преобразование рациональных выражений – это применение тождественных преобразований, с целью упростить запись выражения (сделать его короче и удобнее для дальнейших вычислений).
Напомню тождественные преобразования, которые мы уже умеем выполнять:
- приведение подобных слагаемых;
- раскрытие скобок;
- разложение на множители;
- приведение рациональных дробей к общему знаменателю.
Для преобразования рациональных выражений принимают тот же порядок выполнения действий, что и при преобразовании числовых выражений. Т.е. первыми выполняют действия в скобках, вторыми – действия второй ступени (это умножение, деление, возведение в степень), а затем уже действия первой ступени (сложение, вычитание).
Ещё для преобразования рациональных выражений необходимы знания формул сокращённого умножения и тождества, которые доказали на прошлых уроках:

Задание 1: преобразуйте выражение в рациональную дробь 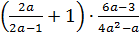 .
.
Решение:
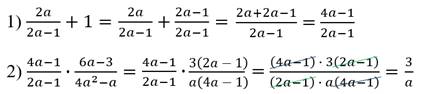
Задание 2: упростите выражение 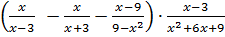 .
.
Решение:
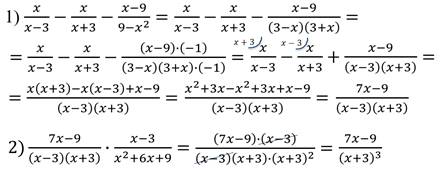
Задание 3: доказать тождество 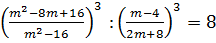 .
.
Решение: доказать тождество – это значит установить, что при всех допустимых значениях переменных его левая и правая части равны. Есть несколько способов доказательства тождеств:
1) Можно преобразовать левую часть и в итоге получить правую.
2) Можно преобразовать правую часть и в итоге получить левую.
3) Можно по отдельности преобразовать правую и левую части и в итоге получить и в первом и во втором случае одно и то же выражение.
4) Можно составить разность левой и правой частей и в результате её преобразований должны получить нуль.
Какой способ выбрать зависит от конкретного тождества, которое требуется доказать.
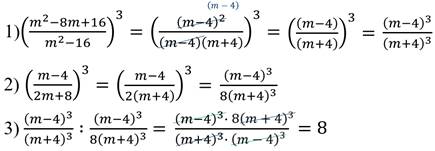
Итоги:
Преобразование рациональных выражений – это применение тождественных преобразований, с целью упростить запись выражения.
Есть несколько способов доказательства тождеств:
1) Можно преобразовать левую часть и в итоге получить правую.
2) Можно преобразовать правую часть и в итоге получить левую.
3) Можно по отдельности преобразовать правую и левую части и в итоге получить и в первом и во втором случае одно и то же выражение.
4) Можно составить разность левой и правой частей и в результате её преобразований должны получить нуль.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 16060
16060

