Данная тема посвящена решению задач на тему «Работа в термодинамике».
Задача 1. Над 3 моль идеального газа проведен процесс, график которого в системе координат (p; V) представлен на рисунке. Определите работу, совершенную газом.

РЕШЕНИЕ
Работа, выполненная газом в системе координат (p; V), численно равна площади фигуры (в нашем случае трапеции), ограниченной графиком процесса, осью абсцисс и ординатами, соответствующими начальному и конечному состоянию системы.

Выпишем начальные и конечные параметры газа, основываясь на данных из графика процесса.

Тогда работа равна

Ответ: работа, совершенная газом, равна 2 кДж.
Задача 2. При изобарном процессе температура идеального газа уменьшается в два раза. Как изменится работа, совершенная над газом, если его первоначальную температуру увеличить вдвое?
|
ДАНО:
|
РЕШЕНИЕ Запишем формулу для вычисления работы, совершаемой газом, при изобарном процессе
На основании уравнения Менделеева — Клапейрона:
Тогда
Составим уравнения для работы газа для двух процессов
Работа внешних сил:
Тогда
И
|
|
|
Ответ: работа, совершенная над газом, увеличится в 3 раза.
Задача 3. Азот массой 14 г, молярная масса которого 28 г/моль, находится в сосуде при температуре 543 К. После изохорного охлаждения, в результате которого давление уменьшается в 3 раза, азот испытывает изобарное расширение, причем температура газа становится равной первоначальной. Изобразите графически эти процессы в координатах (p, V ) и вычислите совершенную газом работу.
|
ДАНО:
|
РЕШЕНИЕ В условии задачи говорится о том, что изначально азот изохорно охлаждают и давление газа, в результате этого процесса, уменьшается. Напомним, что изохорный процесс — это процесс при постоянном объеме. Поэтому графиком данного процесса будет являться прямая линия, параллельная оси ординат. В дальнейшем газ изобарно расширяют. Иными словами, увеличивают его объем при постоянном давлении. Поэтому график этого процесса параллелен оси абсцисс. При этом нам следует учесть то, что в результате изобарного расширения температура газа становится равной первоначальной. Значит точка один и точка три должны лежат на одной изотерме. С учётом этих рассуждений графически эти процессы будут выглядеть следующим образом
Поскольку при изохорном процессе работа не совершается, то совершенная в процессе 1–2–3 работа, равна работе газа при его изобарном расширении
Из уравнения состояния
Тогда работа газа
|
|
|
Ответ: А = 1,5 кДж.
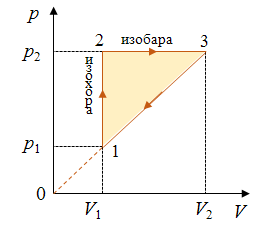
Задача 4. Идеальный газ в количестве v моль совершает цикл, представленный на графике. Отношение давлений в состояниях 2 и 1 равно k. Температура газа в состоянии 3 равна Т3. Определите полезную работу, совершенной газом за цикл.
|
ДАНО:
|
РЕШЕНИЕ Искомая полезная работа газа равна площади фигуры, ограниченной циклом. В данной задаче — это прямоугольный треугольник, то его площадь можно найти как половину произведения катетов.
В результате процесса 1–2 происходит увеличение давления газа. Так как объем газа в результате этого процесса не изменяется, то можно с уверенностью сказать, что процесс 1–2 — это изохорный процесс. В результате процесса 2–3 происходит расширение газа при неизменном давлении. Значит этот процесс изобарный. точки один и три находятся на одной прямой, проходящей через начало координат, уравнение которой можно представить в виде
Тогда
Закон Гей-Люссака для изобарного процесса
Тогда полезная работа равна
Уравнение состояния газа в точке 1
Закон Шарля
Тогда уравнении Менделеева-Клапейрона
Полезная работа равна
|
|
|
Задача 5. 0,5 моль газа совершают круговой процесс, график которого представлен на рисунке. Какая работа может быть совершена за один цикл при таком процессе, если наименьшая температура газа 0 оС, а наибольшая — 127 оС? При температуре 0 оС объем газа 5 л, а при 127 оС — 6 л.

|
ДАНО:
|
СИ
|
РЕШЕНИЕ Для определения работы газа изобразим круговой процесс в координатах p–V
Теперь работу газа можно определить, как площадь фигуры, ограниченной графиком процесса и осями координат. Исходя из графика процессы 1–2 и 3–4 – изохорные, т.к. в них объём не изменяется процессы 2–3 и 4–1 – изобарные, т.к. в них давление не изменяется На графике хорошо видно, что работа, совершаемая газом при
расширении, положительна и численно равна площади, ограниченной графиком Работа, совершаемая газом при сжатии, отрицательна и
численно равна площади, ограниченной графиком Суммарная работа, совершенная газом, равна разности этих площадей, то есть численно равна площади прямоугольника bcdeb.
Запишем уравнения Менделеева — Клапейрона для состояний, которым на графике соответствуют точки 1 и 3
Проверим размерности
|
|
|
Ответ: работа газа за цикл равна 50 Дж.

 Получите свидетельство
Получите свидетельство Вход
Вход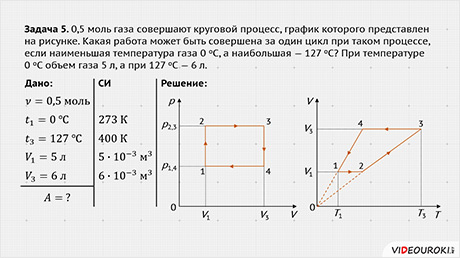




















































 , осью V и отрезками ac и fd.
, осью V и отрезками ac и fd. ,
осью V и
отрезками ab и fe.
,
осью V и
отрезками ab и fe.








 0
0 6705
6705

