Показательные неравенства

Вопросы занятия:

·  рассмотреть основные виды показательных неравенств;

·  разобрать основные методы решения таких неравенств.

Материал урока

Давайте определим, какие же неравенства мы будем называть показательными?

Определение.

Показательными неравенствами называют неравенства вида:

и неравенства, сводящиеся к этому виду.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним, какую же функцию мы называем показательной, как выглядит её график и основные свойства показательной функции.

Одно из свойств показательной функции – это свойство монотонности.

Если a > 1, то функция возрастающая на всей области определения.

Если 0 < a < 1, то функция убывает на всей области определения.

То есть выполняются следующие утверждения (поскольку эта тема неразрывно связана с темой «Показательные уравнения», то нумерацию теорем мы продолжим):

Теорема 2.

Если a > 1, то показательное неравенство:

равносильно неравенству

Если 0 < a < 1, то показательное неравенство:

равносильно неравенству

Рассмотрим несколько примеров.

Пример.

Пример.

Пример.

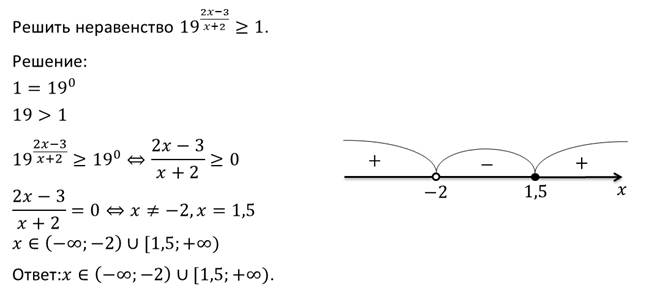
Пример.

Пример.

Пример.