Напомним, что основным тригонометрическим тождеством называется равенство
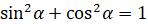 .
.
Это равенство выполняется при любых значениях 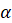 .
.
Из основного тригонометрического тождества можно выразить:
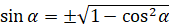 ,
,
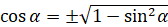 .
.
Знак перед корнем определяется знаком выражения в левой части.
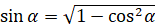 , если
, если 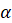 –
угол I или II четверти,
–
угол I или II четверти,
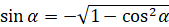 , если
, если 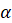 –
угол III или IV четверти.
–
угол III или IV четверти.
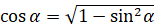 , если
, если 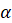 – угол I или IV четверти,
– угол I или IV четверти,
 , если
, если 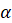 –
угол II или III четверти.
–
угол II или III четверти.
Следующее тождество выражает зависимость между тангенсом и котангенсом:
 .
.
Оно справедливо при всех 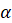 ,
кроме
,
кроме  ,
,  .
.
Следующее равенство устанавливает связь между косинусом и тангенсом одного и того же угла:
 .
.
При этом  ,
,  .
.
И следующее равенство устанавливает связь между синусом и котангенсом:
 .
.
Здесь  ,
,  .
.
Далее напомним формулы приведения.

Данные формулы позволяют свести вычисление синуса, косинуса, тангенса и котангенса любого угла к вычислению их значений для острого угла.
Теперь вспомним формулы сложения.
Формула синуса суммы двух углов:  .
.
Формула синуса разности двух углов:  .
.
Формула косинуса суммы двух углов:  .
.
Формула косинуса разности двух углов:  .
.
Эти формулы справедливы для любых углов 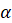 и
и  .
.
Формула тангенса суммы двух углов:
 ,
, 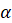 ,
,  ,
,  ,
,  .
.
Формула тангенса разности двух углов:
 ,
, 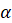 ,
,  ,
,  ,
,  .
.
Формула котангенса суммы двух углов:
 ,
, 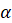 ,
,  ,
,  ,
,  .
.
Формула котангенса разности двух углов:
 ,
, 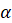 ,
,  ,
,  ,
,  .
.
Напомним формулы синуса, косинуса, тангенса и котангенса двойного угла:
 ;
;
 ;
;
 ,
,  ,
,  ,
,  ;
;
 ,
,  ,
,  .
.
Следующие формулы – формулы суммы и разности синусов:
 ,
,
 .
.
И формулы суммы и разности косинусов:
 ,
,
 .
.
Они
справедливы для любых углов 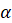 и
и  .
.
Все приведённые выше формулы используются в преобразованиях тригонометрических выражений.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание
первое. Вычислите  ,
,  и
и  , если
, если  и
и  .
.
Решение.

Задание второе. Упростите выражения:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
Решение.


Задание третье. Вычислите, используя формулы приведения:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Решение.
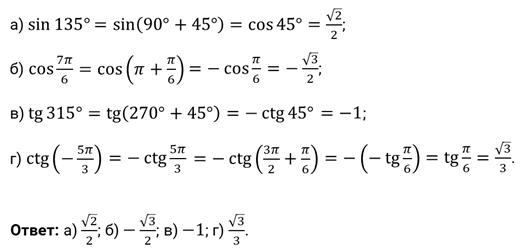
Задание четвёртое. Вычислите:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Решение.


Задание пятое. Найдите значения выражений:
а)
 ;
;
б)
 ;
;
в)
 .
.
Решение.

Задание
шестое. Вычислите  , если
, если  и
и  .
.
Решение.

Задание седьмое. Найдите значения выражений:
а) 
 ; б)
; б)  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход




 4316
4316