Преобразование тригонометрических выражений

На прошлом занятии мы с вами вспомнили основные тригонометрические формулы.

В преобразованиях тригонометрических выражений также используются формулы синуса, косинуса и тангенса половинного угла:

,

,

, , .

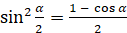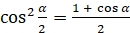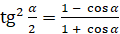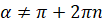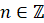Формулы синуса и косинуса половинного угла справедливы для любого угла .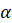

Напомним также формулы, которые называют формулами универсальной тригонометрической подстановки:

, , ;

, , ;

, , , , .

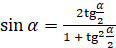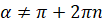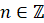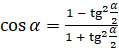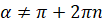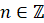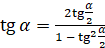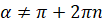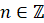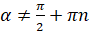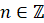По этим формулам можно находить синус, косинус и тангенс угла 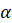, зная тангенс угла .

И вспомним формулы преобразования произведения в сумму или разность:

,

,

.

Эти формулы справедливы для любых углов 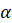 и .

Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.

Задание первое. Найдите значения выражений:

а) ;

б) ;

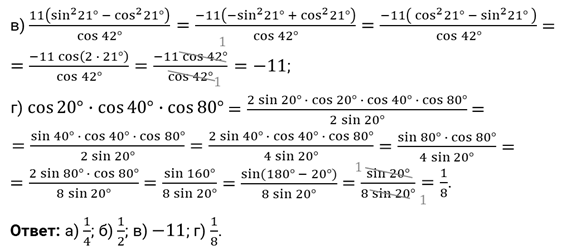
в) ;

г) .

Решение.

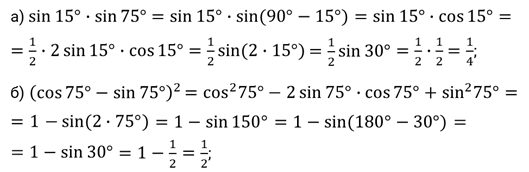
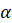Задание второе. Вычислите , если , ,  и  – углы II четверти.

Решение.

Задание третье. Найдите значение выражений:

а) ;

б) ;

в) .

Решение.

Задание четвёртое. Найдите значения выражений:

а) ; б) .

Решение.

Задание пятое. Вычислите: .

Решение.

Задание шестое. Найдите значения выражений:

а) ; б) .

Решение.

Задание седьмое. Найдите ,  и , если .

Решение.