Напомним, что логарифмом положительного числа 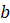 по основанию
А,
по основанию
А,  , где
, где 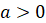 ,
, 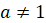 , называется
показатель степени, в которую надо возвести число
, называется
показатель степени, в которую надо возвести число  , чтобы
получить число
, чтобы
получить число 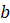 .
.
Например, 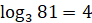 , так как
, так как 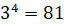 ;
;
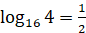 , так как
, так как  .
.
Отметим,
что 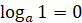 , а
, а 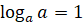 .
.
Из
определения логарифма следует тождество  ,
, 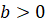 ,
, 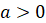 и
и 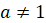 , которое называют основным
логарифмическим тождеством.
, которое называют основным
логарифмическим тождеством.
Действие нахождения логарифма числа называют логарифмированием. А действие нахождения числа по его логарифму называют потенцированием.
Десятичным
логарифмом числа называют логарифм этого числа по основанию 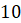 .
.
Натуральным
логарифмом числа называют логарифм этого числа по основанию 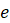 ,
где
,
где  ,
, 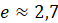 .
.
Напомним также основные свойства логарифмов.
1.
 ,
, 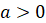 ,
, 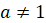 ,
, 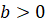 ,
,  .
.
2.
 ,
, 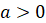 ,
, 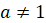 ,
, 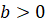 ,
,  .
.
3.
 ,
, 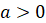 ,
, 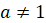 ,
, 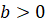 ,
,  .
.
4.
 ,
, 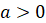 ,
, 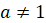 ,
, 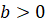 ,
,  .
.
5.
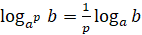 ,
, 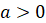 ,
, 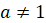 ,
, 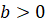 ,
,  .
.
Также вспомним формулу перехода от логарифма по одному основанию к логарифму по другому основанию:
 ,
, 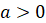 ,
, 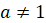 ,
, 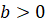 ,
,  ,
,  .
.
Из
этой формулы следует, что  ,
, 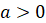 ,
, 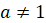 ,
, 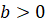 ,
,  .
.
Также
из формулы перехода от логарифма по одному основанию к логарифму по другому
основанию при  и при
и при  получаются
формулы перехода к десятичным и натуральным логарифмам:
получаются
формулы перехода к десятичным и натуральным логарифмам:
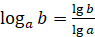 ,
, 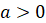 ,
, 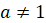 ,
, 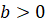 ;
;
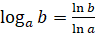 ,
, 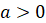 ,
, 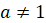 ,
, 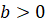 .
.
Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.
Задание первое. Вычислите:
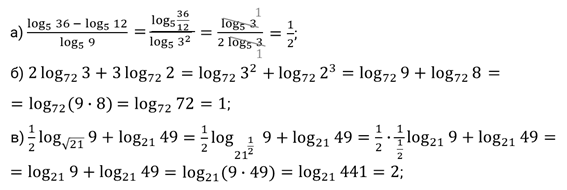
а)
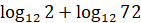 ;
;
б)
 ;
;
в)
 ;
;
г)
 ;
;
д)
 .
.
Решение.

Задание второе. Найдите значения выражений:
а)
 ;
;
б)
 ;
;
в)
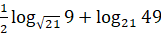 ;
;
г)
 .
.
Решение.
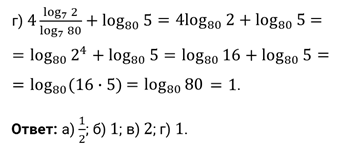
Задание
третье. Вычислите:  .
.
Решение.

Задание
четвёртое. Найдите значение выражения:  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход




 2788
2788

