Напомним, что градусом называют величину
центрального угла, которому соответствует 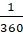 часть окружности.
Градусная мера угла – это положительное число, которое показывает,
сколько раз градус и его части укладываются в измеряемом угле.
часть окружности.
Градусная мера угла – это положительное число, которое показывает,
сколько раз градус и его части укладываются в измеряемом угле.
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.
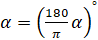 –
формула перехода от радианной меры к градусной.
–
формула перехода от радианной меры к градусной.
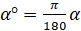 рад
– формула перехода от градусной меры к радианной.
рад
– формула перехода от градусной меры к радианной.
Угол
в 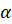 рад стягивает
дугу длиной
рад стягивает
дугу длиной 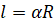 .
.
Также
вспомним, что при повороте точки 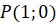 на угол
на угол 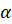 рад, где
рад, где 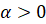 , точка двигается
по единичной окружности против часовой стрелки, проходит путь длиной
, точка двигается
по единичной окружности против часовой стрелки, проходит путь длиной 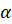 и оказывается в
точке
и оказывается в
точке 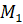 .
.
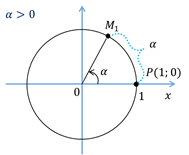
При
повороте точки 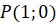 на угол
на угол 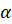 рад, где
рад, где  , точка двигается
по единичной окружности по часовой стрелке, проходит путь длиной
, точка двигается
по единичной окружности по часовой стрелке, проходит путь длиной  и оказывается в
точке
и оказывается в
точке  .
.

Поворот
на  рад означает, что
точка остаётся на месте. Угол поворота можно задавать как в радианах, так и в
градусах.
рад означает, что
точка остаётся на месте. Угол поворота можно задавать как в радианах, так и в
градусах.
Если угол 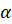 можно
представить как
можно
представить как  , где
, где  –
целое число, то при повороте на угол
–
целое число, то при повороте на угол 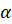 получаем
ту же самую точку, что и при повороте на угол
получаем
ту же самую точку, что и при повороте на угол  .
.
Вы знаете, что синусом угла 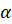 называется
ордината точки
называется
ордината точки  единичной
окружности, полученной поворотом точки
единичной
окружности, полученной поворотом точки  вокруг
начала координат на угол
вокруг
начала координат на угол 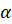 .
.
Косинусом угла 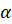 называется
абсцисса точки
называется
абсцисса точки  единичной
окружности, полученной поворотом точки
единичной
окружности, полученной поворотом точки  вокруг
начала координат на угол
вокруг
начала координат на угол 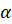 .
.
Тангенсом угла 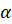 называется
отношение синуса угла
называется
отношение синуса угла 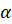 к его
косинусу.
к его
косинусу.
Котангенсом угла 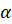 называется
отношение косинуса угла
называется
отношение косинуса угла 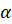 к его
синусу.
к его
синусу.
В этих определениях угол 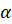 может
выражаться как в градусах, так и в радианах.
может
выражаться как в градусах, так и в радианах.

Важно помнить, что  и
и  определены
для любого угла
определены
для любого угла 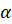 , а их
значения заключены в промежутках от
, а их
значения заключены в промежутках от  до
до  , так
как координаты точек единичной окружности заключены в промежутках от
, так
как координаты точек единичной окружности заключены в промежутках от  до
до  .
.
 определён
для любых углов, кроме
определён
для любых углов, кроме  ,
,  .
.
 определён
для любых углов, кроме
определён
для любых углов, кроме  ,
,  .
.
Отметим,
что синусом, косинусом, тангенсом и котангенсом числа  называется число,
которое соответственно равно синусу, косинусу, тангенсу и котангенсу угла в
называется число,
которое соответственно равно синусу, косинусу, тангенсу и котангенсу угла в  радиан.
радиан.
Приведём таблицу часто встречающихся значений синуса, косинуса, тангенса и котангенса.

Также вспомним, что синус в первой и второй четвертях принимает положительные значения, а в третьей и четвёртой – отрицательные. Косинус принимает положительные значения в первой и четвёртой четвертях, отрицательные значения – во второй и третьей четвертях. Тангенс и котангенс принимают положительные значения в первой и третьей четвертях, а отрицательные значения – во второй и четвёртой четвертях.
Следующие формулы позволяют сводить вычисление значений синуса, косинуса, тангенса и котангенса отрицательных углов к вычислению их значений для положительных углов.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задние
первое. Переведите из радианной меры в градусную: а)  ; б)
; б)  .
.
Решение.

Задание
второе. Переведите из градусной меры в радианную: а)  ; б)
; б)  .
.
Решение.

Задание
третье. Вычислите радиус окружности, если её дуга  м содержит
м содержит  рад.
рад.
Решение.

Задание
четвёртое. Найти координаты точки,
полученной поворотом точки 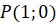 на
угол: а)
на
угол: а)  ; б)
; б)  .
.
Решение.

Задание пятое. Найдите значения выражений:
а)
 ;
;
б)
 ;
;
в)
 .
.
Решение.



Задание шестое. Определите знаки синуса, косинуса и тангенса углов:
а)  ; б)
; б)  ; в)
; в)  .
.
Решение.



 Получите свидетельство
Получите свидетельство Вход
Вход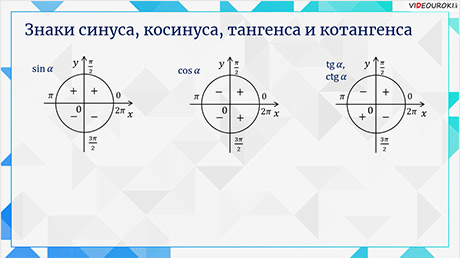




 8204
8204