Напомним, что график – это чертёж, который применяют для наглядного изображения зависимости какой-либо одной величины от другой. Другими словами, график – это линия, которая даёт наглядное представление о характере изменения функции или о каких-либо табличных данных.
Как правило, график располагают на координатной плоскости, в которой горизонтальная ось называется осью абсцисс, вертикальная ось – осью ординат.
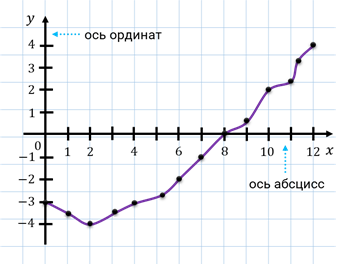
Для работы с графиками главное:
1. Внимательно посмотреть, какая величина откладывается по оси абсцисс, а какая – по оси ординат.
2. Определить цену деления на осях координат, то есть разобраться, что означает одно деление на осях.
3. Ответить на вопрос, используя график.
Также напомним, что диаграмма — графическое представление данных, позволяющее быстро оценить соотношение нескольких величин.
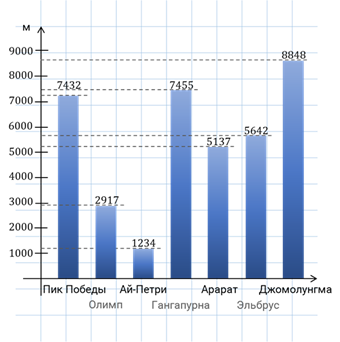
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание
первое. На рисунке жирными точками показана среднесуточная
температура воздуха в Риге за каждый день с 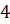 по
по
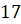 апреля
апреля
 года.
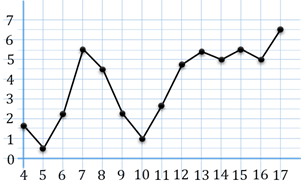
По горизонтали указаны числа месяца, по вертикали – температура в градусах
Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку,
какого числа среднесуточная температура была наименьшей за данный период.
года.
По горизонтали указаны числа месяца, по вертикали – температура в градусах
Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку,
какого числа среднесуточная температура была наименьшей за данный период.
Решение.
Так как в вопросе задачи нас просят определить, какого числа среднесуточная
температура была наименьшей за данный период, то на графике нам необходимо найти
точку, где значение по оси ординат будет наименьшим, то есть найти такую точку,
которая будет расположена ниже всех остальных. Нужная нам точка имеет
координаты 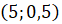 .
Числа месяца отмечены на горизонтальной оси. Следовательно, пятого числа
среднесуточная температура была наименьшей за данный период.
.
Числа месяца отмечены на горизонтальной оси. Следовательно, пятого числа
среднесуточная температура была наименьшей за данный период.
В ответе запишем 5.
Задание
второе. На рисунке жирными точками показана цена золота на
момент закрытия биржевых торгов во все рабочие дни с 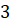 по
по
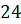 октября
октября
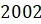 года.
По горизонтали указываются числа месяца, по вертикали — цена золота в долларах
США за унцию. Для наглядности жирные точки на рисунке соединены линией.
Определите по рисунку наименьшую цену золота на момент закрытия торгов за
данный период. Ответ дайте в долларах США за унцию.
года.
По горизонтали указываются числа месяца, по вертикали — цена золота в долларах
США за унцию. Для наглядности жирные точки на рисунке соединены линией.
Определите по рисунку наименьшую цену золота на момент закрытия торгов за
данный период. Ответ дайте в долларах США за унцию.

Решение. Цена золота отмечена на вертикальной оси, а числа месяца – на горизонтальной. Так как в вопросе задачи нас просят определить наименьшую цену золота, то на графике нам необходимо найти точку, значение которой по оси ординат будет наименьшим, то есть найти такую точку, которая будет расположена ниже всех остальных. Видим, что нужная точка расположена в промежутке между числами 312 и 310.
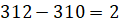 ,
,
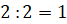 .
.
То есть цена деления одной клеточки равна 1 доллару США за унцию. Тогда понятно, что искомая цена золота составляет 311 долларов США за унцию.
В ответе запишем 311.
Задание
третье. На рисунке жирными точками показана цена нефти на
момент закрытия биржевых торгов во все рабочие дни с 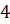 по
по
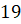 апреля
апреля
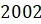 года.
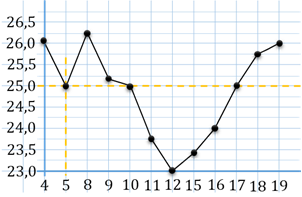
По горизонтали указываются числа месяца, по вертикали – цена барреля нефти в
долларах США. Для наглядности жирные точки на рисунке соединены линиями.
Определите по рисунку, какого числа цена нефти на момент закрытия торгов
впервые за данный период составила 25 долларов за баррель.
года.
По горизонтали указываются числа месяца, по вертикали – цена барреля нефти в
долларах США. Для наглядности жирные точки на рисунке соединены линиями.
Определите по рисунку, какого числа цена нефти на момент закрытия торгов
впервые за данный период составила 25 долларов за баррель.
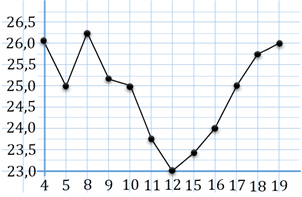
Решение. Чтобы ответить на вопрос задачи, нам нужно на вертикальной оси найти число 25, то есть 25 долларов за баррель. Мы смотрим на график и прокладываем горизонтальную черту на уровне 25. Обратите внимание, нашим ответом будет первая точка, которая будет на проведённой нами прямой, то есть самая левая. Итак, находим эту точку. Затем проводим вертикальную прямую до пересечения с осью абсцисс. И видим, что 5-го числа цена нефти на момент закрытия торгов впервые за данный период составила 25 долларов за баррель.
В ответе запишем 5.
Задание
четвёртое. На рисунке жирными точками показана цена серебра,
установленная Центробанком Российской Федерации, во все рабочие дни в октябре  года.
По горизонтали указываются числа месяца, по вертикали – цена серебра в рублях
за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите
по рисунку, сколько дней из данного периода цена серебра была между
года.
По горизонтали указываются числа месяца, по вертикали – цена серебра в рублях
за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите
по рисунку, сколько дней из данного периода цена серебра была между 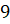 и
и
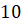 рублями
за грамм.
рублями
за грамм.

Решение.
Чтобы ответить на вопрос задачи, нам нужно найти все те дни, которые будут
относиться к промежутку между 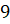 и
и
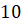 рублями
за грамм. Для этого на вертикальной оси мы найдём числа 9 и 10, то есть 9 и 10
рублей за грамм. Затем проведём горизонтальные линии на уровне этих чисел.
Обратите внимание, последний день, когда цена серебра за грамм была между
рублями
за грамм. Для этого на вертикальной оси мы найдём числа 9 и 10, то есть 9 и 10
рублей за грамм. Затем проведём горизонтальные линии на уровне этих чисел.
Обратите внимание, последний день, когда цена серебра за грамм была между 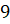 и
и
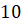 рублями
– это 17 число. Также следует отметить, что за этот период цена серебра за
грамм 15 числа была меньше 9 рублей. Значит, этот день нам нужно будет
исключить. Итак, теперь посчитаем, сколько же рабочих дней из данного периода
цена серебра была между девятью и десятью рублями за грамм. В результате
получим 8 рабочих дней.
рублями
– это 17 число. Также следует отметить, что за этот период цена серебра за
грамм 15 числа была меньше 9 рублей. Значит, этот день нам нужно будет
исключить. Итак, теперь посчитаем, сколько же рабочих дней из данного периода
цена серебра была между девятью и десятью рублями за грамм. В результате
получим 8 рабочих дней.
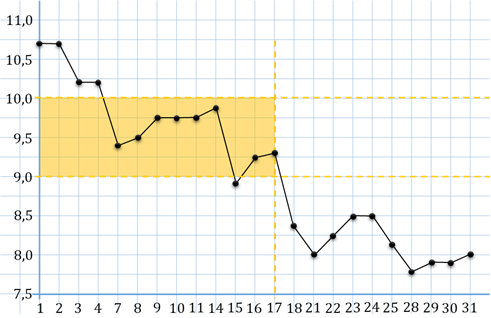
В ответе запишем 8.
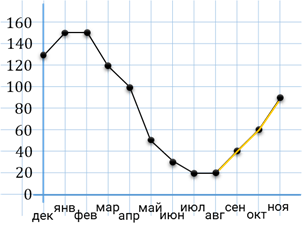
Задание пятое. На рисунке точками показаны объёмы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных обогревателей. Для наглядности точки соединены линией. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.
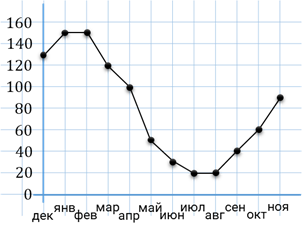
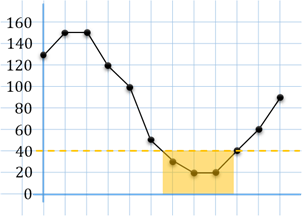
Решение. Итак, прочитаем первую характеристику. Нам нужно найти период, когда ежемесячный объём продаж был меньше 40 штук в течение всего периода. Количество проданных обогревателей отмечено на вертикальной оси. Тогда найдём на вертикальной оси число 40 и проведём горизонтальную линию на уровне этого числа. По графику видно, что период, когда ежемесячный объём продаж был меньше 40 штук, приходился на лето.
Перейдём ко второй характеристике. Здесь нам нужно найти период, когда ежемесячный объём продаж достиг максимума. Для этого на графике нам необходимо найти точку, значение которой по оси ординат будет наибольшим, то есть найти такую точку, которая будет расположена выше всех остальных. Видим, на графике есть две такие точки. Проведём из этих точек вертикальные линии до пересечения с осью абсцисс. Теперь понятно, что в январе и феврале ежемесячный объём продаж достиг максимума. А эти два месяца относятся к зиме.
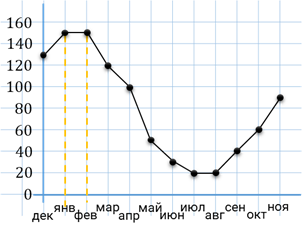
Следующая характеристика: ежемесячный объём продаж падал в течение всего периода. На горизонтальной оси указаны месяцы. Рассмотрим внимательно график и найдём такой промежуток, в котором график постоянно идёт вниз. Несложно заметить, что график постоянно идёт вниз в марте, апреле и мае. А эти месяцы относятся к весне.
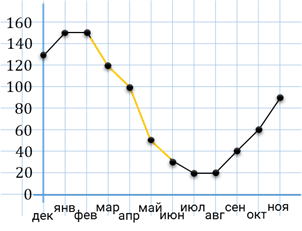
И последняя характеристика: ежемесячный объём продаж рос в течение всего периода. В этом случае нам нужно найти такой промежуток графика, в котором график постоянно идёт вверх. Внимательно посмотрев на график, видно, что в сентябре, октябре и ноябре график постоянно идёт вверх. А эти месяцы относятся к осени.
Задание
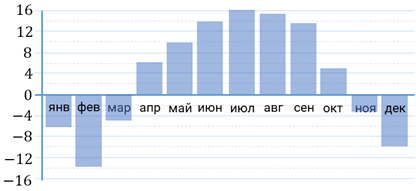
шестое. На диаграмме показана среднемесячная температура
воздуха в Нижнем Новгороде за каждый месяц 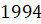 года.
По горизонтали указываются месяцы, по вертикали – температура в градусах
Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в
года.
По горизонтали указываются месяцы, по вертикали – температура в градусах
Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 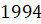 году.
Ответ дайте в градусах Цельсия.
году.
Ответ дайте в градусах Цельсия.
Решение.
Температура откладывается по оси ординат. Поэтому нам нужна самая высшая точка
на диаграмме. Мы видим, что самый длинный столбик, направленный вверх,
находится на уровне седьмого месяца. Понятно, что искомая среднемесячная
температура составляет 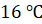 .
.
В
ответе запишем 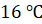 .
.
Задание
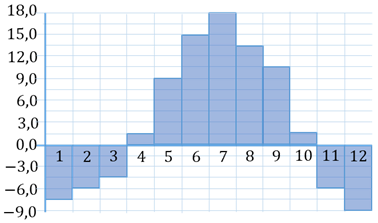
седьмое. Среднемесячная температура воздуха в Ижевске за
каждый месяц 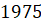 года
показана на диаграмме. По горизонтали указываются месяцы, по вертикали –
температура в градусах Цельсия. Определите по диаграмме среднюю температуру
летом
года
показана на диаграмме. По горизонтали указываются месяцы, по вертикали –
температура в градусах Цельсия. Определите по диаграмме среднюю температуру
летом 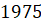 года.
года.
Решение.
На горизонтальной оси отмечены месяцы. Напомним, что к летним месяцам относятся
шестой, седьмой и восьмой месяцы. На вертикальной оси указана температура.
Тогда столбику, расположенному в шестом месяце, соответствует температура 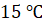 ,
столбику, расположенному в седьмом месяце, – 1
,
столбику, расположенному в седьмом месяце, – 1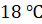 .
А вот значение градусов, соответствующее столбику, расположенному в восьмом
месяце, находится между
.
А вот значение градусов, соответствующее столбику, расположенному в восьмом
месяце, находится между 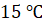 и
и
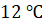 .
Получается, что разность между этими двумя числами равна трём. Эти 3 градуса
нужно разбить на 2 деления. Поэтому понятно, что в одном делении откладывается
.
Получается, что разность между этими двумя числами равна трём. Эти 3 градуса
нужно разбить на 2 деления. Поэтому понятно, что в одном делении откладывается 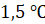 ,
так как
,
так как 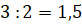 .
Тогда столбику, расположенному в восьмом месяце, соответствует температура
.
Тогда столбику, расположенному в восьмом месяце, соответствует температура 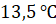 (
(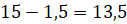 ).
).
Тогда средняя температура за летние месяцы:
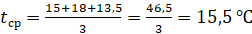 .
.
В
ответе запишем 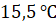 .
.
Задание восьмое. На диаграмме показано среднесуточное количество перевезённых пассажиров в Московском метрополитене за каждый месяц 2008 года (в тысячах человек). Сколько было месяцев, в каждый из которых среднесуточное число перевезённых пассажиров составило не менее 7500 человек?
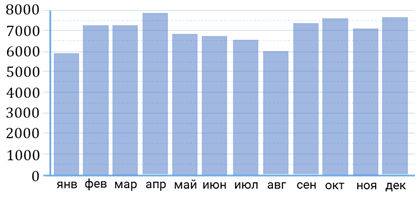
Решение. На вертикальной оси отмечено количество пассажиров, перевезённых в Московском метрополитене. Найдём на вертикальной оси значение 7500. Для этого нам нужно определить цену деления. Так как второму делению на вертикальной оси соответствует отметка в 1000 человек, то цена одного деления будет равна 500. Тогда значение 7500 на вертикальной оси будет расположено посередине между числами 7000 и 8000. Проведём горизонтальную прямую на уровне 7500. И посчитаем, сколько столбиков будут расположены выше нашей линии. Итак, видим, что у нас таких столбиков 3.
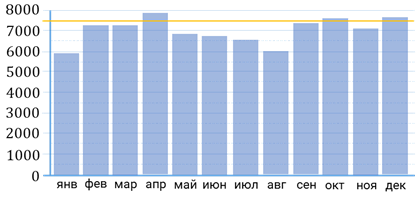
В ответе запишем 3.
Задание девятое. На диаграмме приведены данные о длине восьми крупнейших рек России (в тысячах километров). Первое место по длине занимает река Лена. На каком месте по длине находится река Амур?
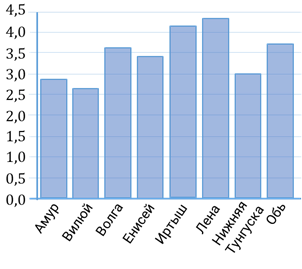
Решение. Для начала расположим названия рек в порядке убывания их длин. Для того чтобы делать это задание не на глаз, давайте приложим линейку к самому высокому столбику и затем будем медленно опускаться вниз, записывая реки в порядке убывания их длин. Итак, первое место – Лена, второе – Иртыш, третье место – Обь, четвёртое – Волга, пятое место – Енисей, шестое – Нижняя Тунгуска, седьмое место – Амур и восьмое – Вилюй. Амур находится на седьмом месте.
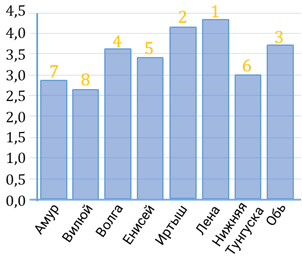
В ответе запишем 7.
В завершение урока хочется сказать, что задания на тему чтение графиков и диаграмм не такие уж и сложные. Чтобы не было ошибок, главное:
1. Внимательно прочитать условие задачи.
2. Определить, относительно какой оси нужно искать искомую величину.
3. Разобраться с ценой деления на осях координат.

 Получите свидетельство
Получите свидетельство Вход
Вход




 4993
4993

