Напомним, что модулем числа называется само это число, если оно неотрицательно,
и противоположное ему число, если оно отрицательно.
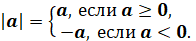
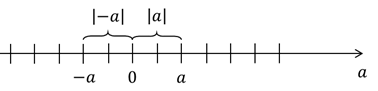
Выделим несколько основных свойств модуля, полезных при решении различных алгебраических и геометрических заданий:
1.
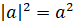 .
.
2.
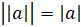 .
.
3.
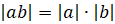 .
.
4.
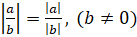 .
.
5.
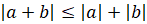 .
.
6.
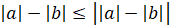 .
.
При извлечении арифметического корня натуральной степени необходимо обращать внимание не только на область допустимых значений выражения (нельзя извлекать корни чётной степени из отрицательных чисел), но и на результат.
Так,
например, 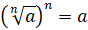 ,
,
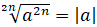 ,
,
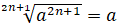 .
.
Также при преобразовании выражений полезно знать и использовать основные свойства арифметических корней.
При
условии, что 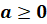 ,
,
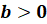 ,
а
,
а 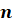 ,
,
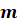 и
и
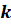 –
натуральные числа, причём
–
натуральные числа, причём 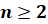 ,
,
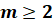 ,
справедливы равенства:
,
справедливы равенства:
1.
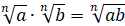 .
(число
.
(число 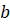 может
также быть равным
может
также быть равным 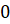 )
)
2.
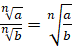 .
.
3.
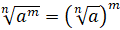 .
(число
.
(число 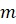 может
быть любым целым, если
может
быть любым целым, если 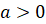 )
)
4.
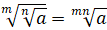 .
.
5.
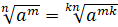 .
.
6.
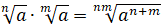 .
.
Используя
формулу связи между арифметическим корнем и степенью с рациональным показателем
для 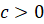 :
:
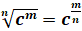
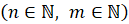 ,
можно переходить от вычислений с корнями к более удобным вычислениям со
степенями, в которых действия опираются на следующие свойства степеней
положительных чисел:
,
можно переходить от вычислений с корнями к более удобным вычислениям со
степенями, в которых действия опираются на следующие свойства степеней
положительных чисел:
1.
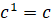 .
.
2.
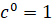 .
.
3.
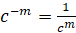 .
.
4.
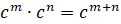 .
.
5.
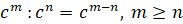 .
.
6.
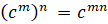 .
.
7.
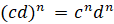 .
.
8.
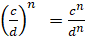 .
.
Эти
равенства справедливы для любых действительных чисел 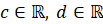 ,
,
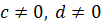 и
для любых
и
для любых 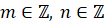 .
.
Также при преобразовании выражений полезно знать и использовать следующие формулы сокращённого умножения:
1.
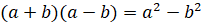 .
.
2.
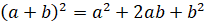 .
.
3. 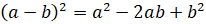 .
.
4. 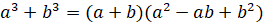 .
.
5.
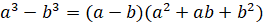 .
.
6.
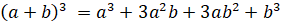 .
.
7.
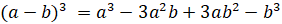 .
.
8. 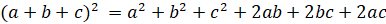 .
.
9. 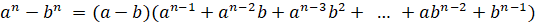 .
.
В
последней формуле нужно обратить внимание на правую скобку: степени 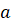 с
каждым шагом на единицу уменьшаются, а степени
с
каждым шагом на единицу уменьшаются, а степени 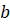 –
увеличиваются.
–
увеличиваются.
При преобразовании выражений конечно же следует не забывать о порядке выполнения действий: при выполнении действий в выражении без скобок сначала выполняют действия большей ступени. Если в нём все действия одной ступени, то их выполняют в том порядке, в котором они записаны, то есть слева направо. Если выражение содержит скобки, то сначала выполняют все действия внутри скобок, начиная с большей ступени.
Действия I ступени – сложение и вычитание.
Действия II ступени – умножение и деление.
Действия III ступени – возведение в степень.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите численное значение выражения
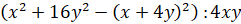 .
.
Решение.

Задание
второе. Найдите значение выражения 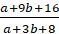 ,
если
,
если 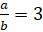 .
.
Решение.

Задание
третье. Найдите значение выражения 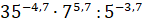 .
.
Решение.
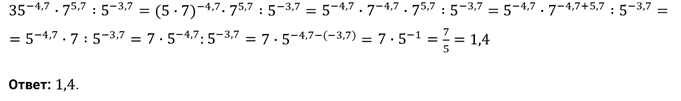
Задание
четвёртое. Найдите значение выражения 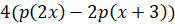 ,
если
,
если 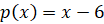 .
.
Решение.
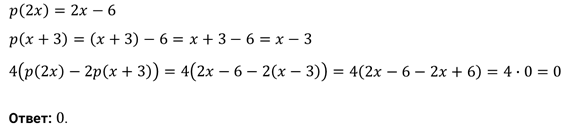
Задание пятое. Найдите численное значение выражения
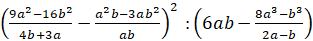 .
.
Решение.
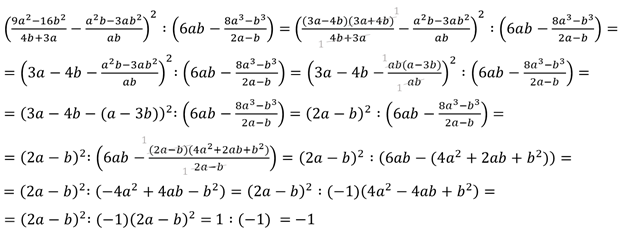
Следует
отметить, что наше первоначальное выражение имеет смысл только при 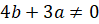 ,
,
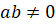 и
и
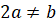 .
.
Задание
шестое. Выражение 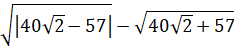 является
целым числом. Найдите это целое число.
является
целым числом. Найдите это целое число.
Решение.
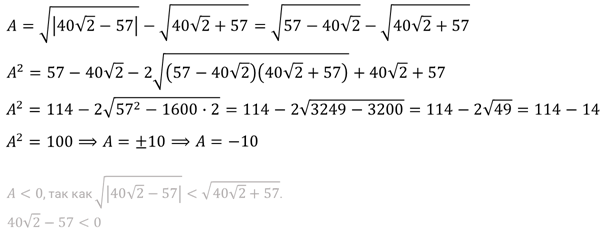

 Получите свидетельство
Получите свидетельство Вход
Вход




 3133
3133

