Напомним, что степенью с натуральным показателем называется произведение

где
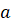 –
основание степени (
–
основание степени (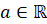 ),
),
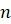 –
показатель степени (
–
показатель степени (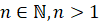 ).
).
Возвести
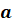 в
в
 -ю
степень – это значит найти значение выражения
-ю
степень – это значит найти значение выражения  .
.
При
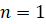 имеем
имеем
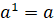 .
.
Степень
с нулевым показателем: 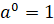 ,
если
,
если 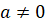 ,
то есть любое число (кроме
,
то есть любое число (кроме 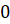 )
в нулевой степени равно
)
в нулевой степени равно 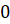 .
.
Выражение
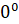 не
имеет смысла.
не
имеет смысла.
Степенью
с отрицательным целым показателем называется число 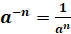 ,
где
,
где 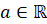 ,
,
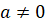 и
и
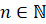 .
.
При возведении отрицательного числа в нечётную степень получится отрицательное число, а при возведении отрицательного числа в чётную степень получится положительное число.
Для
любых действительных чисел 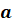 и
и
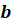 ,
отличных от
,
отличных от 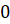 ,
и для любых целых показателей
,
и для любых целых показателей 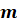 и
и
 имеют
место следующие пять основных свойств степеней:
имеют
место следующие пять основных свойств степеней:
1.
 .
.
2.
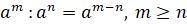 .
.
3.
 .
.
4.
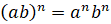 .
.
5.
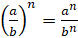 .
.
Используя
степени с целыми показателями, любое положительное число у можно записать в
виде произведения 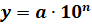 ,
где
,
где 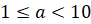 и
и
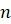 –
целое число. Такая запись называется стандартным видом числа
–
целое число. Такая запись называется стандартным видом числа 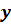 ,
а число
,
а число 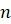 –
порядком числа
–
порядком числа 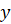 .
.
Также
напомним, что корнем  -й
степени (
-й
степени (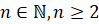 )
из действительного числа
)
из действительного числа 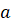 называют
такое действительное число
называют
такое действительное число 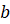 ,
,
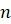 -я
степень которого равна
-я
степень которого равна 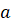 ,
то есть
,
то есть 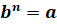 .
.
Арифметическим
корнем  -й
степени (
-й
степени (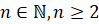 )
из числа
)
из числа 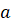 называется
неотрицательное число,
называется
неотрицательное число, 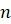 -я
степень которого равна
-я
степень которого равна 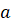 .
Обозначают арифметический корень с помощью знака радикала:
.
Обозначают арифметический корень с помощью знака радикала: 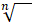 .
.
Под
выражением 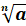 условимся
понимать:
условимся
понимать:
1.
единственное значение корня в случае нечётного 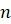 ;
;
2.
арифметический корень в случае чётного 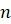 ;
;
3.
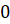 ,
если
,
если 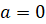 ,
при любом
,
при любом 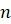 .
.
Заметим,
что  при
нечётном
при
нечётном 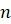 ,
но
,
но 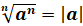 при
чётном
при
чётном 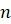 .
.
Так,
например, 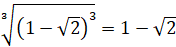 ,
,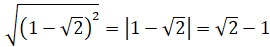 .
.
То
есть 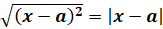 ,
где
,
где 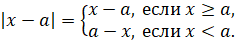
Действие,
посредством которого отыскивается корень 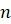 -й
й степени, называется извлечением корня
-й
й степени, называется извлечением корня  -й
степени. Это действие является обратным действию возведения в
-й
степени. Это действие является обратным действию возведения в
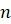 -ю
степень.
-ю
степень.
А
теперь давайте вспомним свойства арифметического корня  -й
степени. Итак, при условии, что
-й
степени. Итак, при условии, что 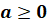 ,
,
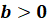 ,
а
,
а  ,
,
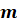 и
и
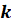 –
натуральные числа, причём
–
натуральные числа, причём  ,
,
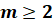 ,
справедливы равенства:
,
справедливы равенства:
1.
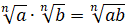 .
(число
.
(число 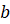 может
также быть равным
может
также быть равным 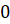 )
)
2.
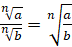 .
.
3.
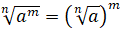 .
(число
.
(число 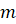 может
быть любым целым, если
может
быть любым целым, если 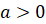 )
)
4.
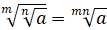 .
.
5.
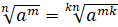 .
.
Также следует вспомнить формулу сложного радикала:
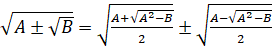 .
.
И
ещё напомним, что степенью с рациональным показателем называется число 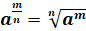 ,
где
,
где 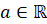 ,
,
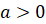 ,
,
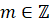 ,
,
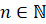 ,
,
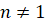 .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите значения выражений:
а)
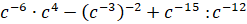 при
при
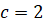 ;
;
б)
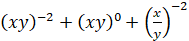 при
при
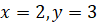 .
.
Решение.
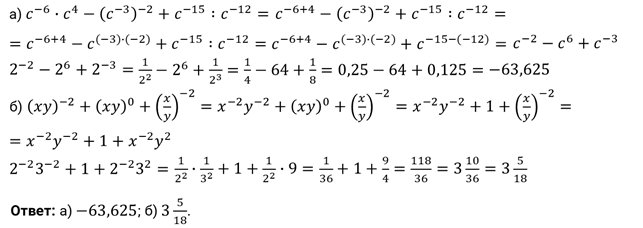
Задание
второе. Вычислите 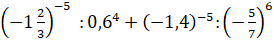 .
.
Решение.
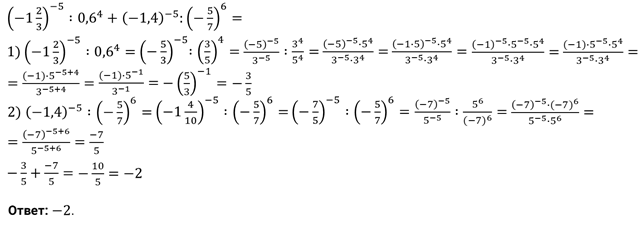
Задание
третье. Упростите выражение 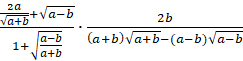 .
.
Решение.
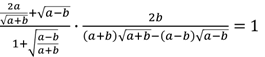




 Получите свидетельство
Получите свидетельство Вход
Вход




 5491
5491