Сегодня на уроке мы вспомним понятия отображения плоскости на себя, движение плоскости, вспомним основные понятия центральной симметрии. Введём понятия отображения пространства и движение пространства, центральной симметрии в пространстве. Определим, будет ли центральная симметрия в пространстве – движением пространства.
Мы уже с вами знакомы с таким понятием, как движение. Давайте вспомним, что мы называли движением.
Движением мы называли любое отображение плоскости, которое сохраняет расстояние между точками.
Отображение плоскости на себя определяли так: если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причём любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя.
Эти определения мы давали для движения на плоскости. Но в стереометрии мы говорим о пространстве, значит, надо определить, что называется движением пространства.
Но сначала давайте определим, что такое отображение пространства на себя.
Определение:
Пусть каждой точке 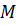 пространства
поставлена в соответствие некоторая точка
пространства
поставлена в соответствие некоторая точка 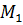 ,
причем любая точка
,
причем любая точка 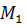 пространства
оказалась поставленной в соответствие какой-то точке
пространства
оказалась поставленной в соответствие какой-то точке 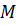 .
Тогда говорят, что задано отображение пространства на себя. При
данном отображении точка
.
Тогда говорят, что задано отображение пространства на себя. При
данном отображении точка 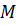 переходит
(отображается) в точку
переходит
(отображается) в точку 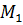 .
.
Определение:
Под движением пространства понимается
отображение пространства на себя, при котором любые две точки пространства 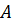 и
и
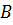 отображаются
в какие-то точки
отображаются
в какие-то точки 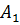 и
и
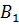 так,
что
так,
что 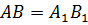 .
.
По-другому можно сказать, что движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.
Теперь давайте вспомним, какие фигуры обладают центральной симметрией.
Определение:
Фигура называется симметричной относительно
точки 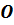 ,
если для каждой точки фигуры симметричная ей точка относительно точки
,
если для каждой точки фигуры симметричная ей точка относительно точки 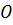 также
принадлежит этой фигуре. Точка
также
принадлежит этой фигуре. Точка 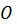 называется
центром симметрии фигуры.
называется
центром симметрии фигуры.
Примерами центрально симметричных фигур можно назвать некоторые цветы:

В геометрии яркими примерами центрально симметричных фигур являются окружность (центр симметрии – центр окружности) и параллелограмм (центром симметрии является точка пересечения диагоналей).

Ещё мы давали такое определение:
Точки 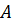 и
и
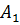 называются
симметричными относительно точки
называются
симметричными относительно точки 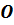 ,
если
,
если 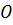 –
середина отрезка
–
середина отрезка 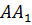 .
.
Точка 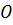 называется
центром симметрии.
называется
центром симметрии.
Точка 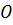 считается
симметричной сама себе.
считается
симметричной сама себе.
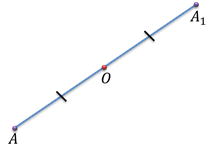
В курсе планиметрии мы доказывали, что центральная симметрия является движением.
Напомним это доказательство.
Рассмотрим точки М и N и точки М1 и N 1 симметричные точкам М и N относительно точки О.
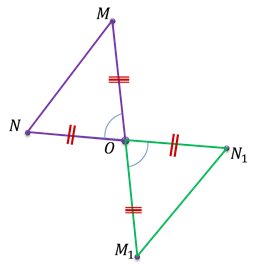
Рассмотрим треугольники М NО и М1ОN1.
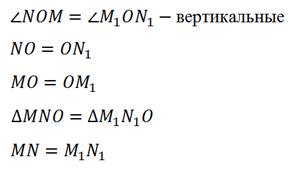
То есть при центральной симметрии сохраняется расстояние между точками. Тогда по определению движения, получим, что и центральная симметрия является движением.
Определение:
В пространстве центральной симметрией
мы назовём отображение пространства на себя, при котором любая точка 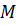 переходит
в симметричную ей точку
переходит
в симметричную ей точку 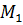 относительно
данного центра
относительно
данного центра 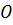 .
.
Теперь давайте докажем, что и в пространстве центральная симметрия является движением.
Пусть О – центр симметрии. Введём прямоугольную систему координат Оxyz с началом в точке О. Теперь давайте попробуем установить связь между координатами двух точек М (x, y, z) и М1(x1, y1, z1), симметричных относительно точки О.

Если точка М не совпадает с точкой О, то по
определению центральной симметрии О – середина отрезка ММ1. Тогда
координаты точки О можно вычислить по формулам координат середины отрезка. С
другой стороны, поскольку О – начало координат, значит, точка О имеет
координаты 0, 0, 0. То есть получим, что 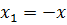 ,
,
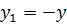 ,
,
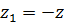 .
.
Если точки М и О совпадают, тогда точка М1
также совпадает с точкой О, потому что точка О – центр симметрии, а, значит,
она отображается сама на себя. И в этом случае будут выполнятся равенства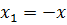 ,
,
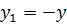 ,
,
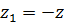 .
.
Теперь давайте рассмотрим две точки 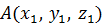 и
и
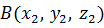 .
.
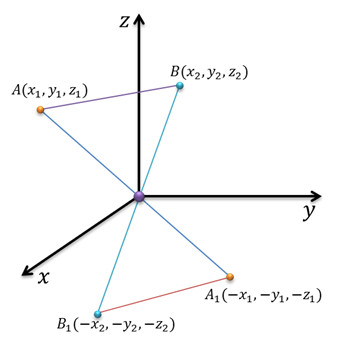
По только что доказанным формулам для координат
симметричных точек получим, что точка 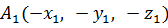 .
Точка
.
Точка 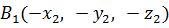 .
.
Теперь давайте найдём расстояние 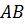 .
Получим, что расстояние между точками
.
Получим, что расстояние между точками 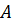 ,
,
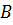 равно:
равно:
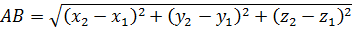
Теперь давайте найдём расстояние между точками 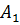 и
и
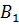 .
.
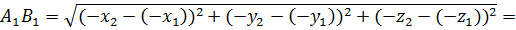
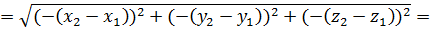
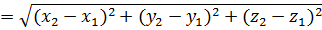
Очевидно, что оба эти выражения равны, то есть
получим, что 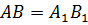 .
.
Вывод: расстояние между точками при центральной симметрии в пространстве сохраняется, значит, центральная симметрия в пространстве также является движением, но уже не плоскости, а пространства.
Рассмотрим несколько задач.
Задача:
найти координаты точек, в которые переходят точки 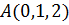 ,
,
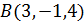 ,
,
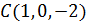 при
центральной симметрии относительно начала координат.
при
центральной симметрии относительно начала координат.
Решение: воспользуемся формулами для вычисления координат симметричных точек.
Если точка 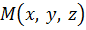 симметрична
точке
симметрична
точке 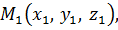 то
справедливы формулы:
то
справедливы формулы:
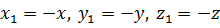 .
.
Тогда получим, что точка 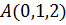 отобразится
в точку
отобразится
в точку 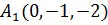 .
.
Точка 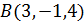 отобразится
в точку
отобразится
в точку 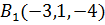 .
.
Точка 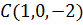 отобразится
в точку
отобразится
в точку 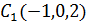 .
.
Решим ещё одну задачу.
Задача: доказать, что при центральной симметрии прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.
Доказательство. Пусть
прямая 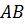 не
проходит через центр симметрии О. Построим точки симметричные точкам
не
проходит через центр симметрии О. Построим точки симметричные точкам 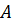 и
и
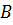 относительно
точки О.
относительно
точки О.
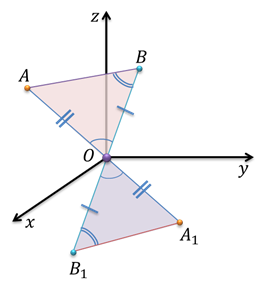
Рассмотрим 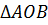 и
и
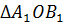 .
По определению центральной симметрии точка О – середина отрезков АА1
и ВВ1, то есть
.
По определению центральной симметрии точка О – середина отрезков АА1
и ВВ1, то есть 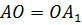 и
и
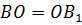 .
.
Углы 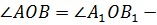 как вертикальные, то
есть треугольники равны по двум сторонам и углу между ними.
как вертикальные, то
есть треугольники равны по двум сторонам и углу между ними.
Тогда получим, что 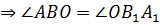 .
Эти углы являются накрестлежащими для прямых
.
Эти углы являются накрестлежащими для прямых 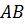 и
и
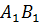 при
секущей
при
секущей 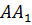 .
Тогда по признаку параллельности прямых получим, что прямые
.
Тогда по признаку параллельности прямых получим, что прямые 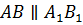 .
Что и требовалось доказать.
.
Что и требовалось доказать.
Итоги:
Сегодня на уроке мы вспомнили понятия отображения плоскости на себя, движение плоскости, вспомнили основные понятия центральной симметрии. Ввели понятия отображения пространства и движение пространства, центральной симметрии в пространстве. Показали, что и в пространстве центральная симметрия будет примером движения.

 Получите свидетельство
Получите свидетельство Вход
Вход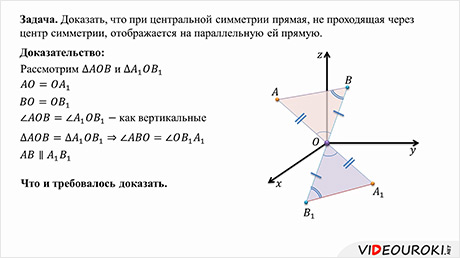



 0
0 16998
16998

