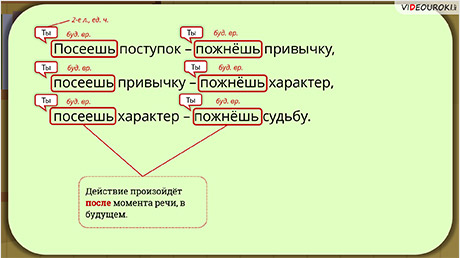
Вы уже знакомы с понятиями угла между прямыми и угла между векторами. А также знаете, что такое двугранный угол и угол между прямой и плоскостью.

Сегодня мы научимся вычислять углы между прямыми, а также между прямой и плоскостью.

Но для начала введём понятие направляющего вектора.
Определение:
Ненулевой вектор называется направляющим вектором прямой а, если он лежит либо на прямой а, либо на прямой, параллельной прямой а.

Понятно, что таких векторов бесконечно много и все они коллинеарны.
Задача: найти угол между прямыми, если известны координаты направляющих векторов этих прямых.
Будем работать с прямыми а и b. Для прямой a направляющим является вектор p, а для прямой b — вектор q.

Итак, возможны два случая.
Если угол  между
направляющими векторами острый, то он равен углу между прямыми
между
направляющими векторами острый, то он равен углу между прямыми  .
.

И если угол  между
направляющими векторами тупой, то угол
между
направляющими векторами тупой, то угол  между
прямыми равен 180о –
между
прямыми равен 180о –  .
.

Так как в первом случае косинус угла между прямыми равен косинусу угла между направляющими векторами, то мы можем вычислить его по известной формуле косинуса угла между векторами.

Ну, а во втором случае записан косинус угла смежного
с углом  .
Косинусы смежных углов противоположны по знаку, поэтому мы получим выражение
противоположное тому, которое было получено в первом случае.
.
Косинусы смежных углов противоположны по знаку, поэтому мы получим выражение
противоположное тому, которое было получено в первом случае.

Угол между прямыми всегда меньше либо равен 90о, поэтому его косинус соответственно будет являться числом неотрицательным. Тогда оба случая можно объединить в один и записать, что косинус угла между прямыми равен частному модуля скалярного произведения направляющих векторов и произведения их длин.

А сейчас найдём угол между прямой и плоскостью, если известны координаты направляющего вектора к прямой и координаты ненулевого вектора, перпендикулярного к плоскости.
Вам уже известно, что углом между прямой и
плоскостью является угол между прямой и её проекцией на эту плоскость.
Обозначим этот угол за  .
А угол между направляющим вектором и вектором, перпендикулярным к плоскости
обозначим за
.
А угол между направляющим вектором и вектором, перпендикулярным к плоскости
обозначим за  .
.

Эти углы в сумме дают 90о (то есть углы  и
и
 являются
дополнительными). А нам известно, что синус угла равен косинусу дополнительного
угла. Это означает, что
являются
дополнительными). А нам известно, что синус угла равен косинусу дополнительного
угла. Это означает, что  .
.

Ну, а  между
векторами
между
векторами  и
и
 мы
без труда найдём по уже известной формуле:
мы
без труда найдём по уже известной формуле:
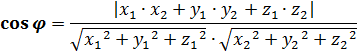
Но ведь возможен и случай, когда угол между
векторами  и
и
 тупой.
тупой.

Тогда углы  и
и
 являются
дополнительными, то есть их сумма равна
являются
дополнительными, то есть их сумма равна  .
.
Отсюда можно записать, что  .
.

Ну, а формула косинуса угла между векторами нам уже известна.
Чтобы объединить две полученных формулы в одну, можно вспомнить, что синус угла от нуля до 180о является числом неотрицательным. Тогда можно записать, что

Таким образом, мы получили формулы косинуса угла между прямыми и синуса угла между прямой и плоскостью. Причём правые части эти формул абсолютно совпадают.
Отличие лишь в том, что две прямые задают направляющие векторы.

А прямую и плоскость — направляющий вектор прямой и вектор, перпендикулярный к плоскости.

Такой вектор называют нормальным вектором к плоскости.
Решим несколько задач.
Задача:
 прямоугольный
параллелепипед, где
прямоугольный
параллелепипед, где  . Найти
. Найти  и
и
 .
.
Решение: ранее в таких случаях мы пытались по рисунку находить величины углов.
Но теперь мы владеем формулой косинуса угла между прямыми.
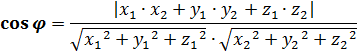
Только для этого необходимо знать координаты
направляющих векторов прямых. В данном случае, для прямой  направляющим
может является вектор
направляющим
может является вектор  ,
а для прямой
,
а для прямой
 —
вектор
—
вектор  .
.

Для удобства изобразим прямоугольную систему
координат так, чтобы точка  совпадала
с точкой начала координат. Взяв длину рёбер
совпадала
с точкой начала координат. Взяв длину рёбер  и
и
 за
единичные отрезки, можно утверждать, что длина отрезка
за
единичные отрезки, можно утверждать, что длина отрезка  равна
2.
равна
2.
Тогда не трудно определить координаты точек  ,
,
 ,
,
 и
и
 .
.
Точка  .
Точка
.
Точка  .
Точка
.
Точка  .
А точка
.
А точка  .
.
Теперь не трудно найти координаты векторов  и
и
 как
разности соответствующих координат конца и начала вектора.
как
разности соответствующих координат конца и начала вектора.
Получаем, что вектор  .
А вектор
.
А вектор  .
.
Теперь можем воспользоваться формулой косинуса угла между прямыми. Подставим координаты направляющих векторов.

А теперь, пользуясь фрагментом из таблицы Брадиса, найдём величину данного угла, помня о том, что поправка для косинуса имеет знак минус:

Итак, угол между прямыми  .
.
Теперь найдём угол между прямыми  и
и
 .
.

В качестве направляющих векторов для данных прямых
удобно взять векторы  и
и
 .
.
Найдём координаты точек  ,
,
 и
и
 .
.
Точка А имеет координаты  .
Точка
.
Точка  .
А точка
.
А точка  .
.
Тогда вектор  .
А вектор
.
А вектор  .
.
Подставим значения координат направляющих векторов в формулу косинуса угла между прямыми.
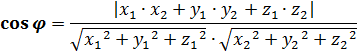
В ходе вычислений получаем

Вычислив примерное значение этой дроби, можем воспользоваться таблицей Брадиса:

Так получаем, что угол между прямыми  .
.
Вот так по координатам направляющих векторов находят величину угла между прямыми.
Задача:
 тетраэдр.
тетраэдр.  .
.
 ,
а
,
а  .
.
Вычислить синус угла между прямой, проходящей через
середины рёбер  и
и
 ,
и плоскостью: а)
,
и плоскостью: а)  ;
б)
;
б)  ;
в)
;
в)  .
.
Решение:
По условию рёбра  ,
,
 и
и
 взаимно
перпендикулярны. Поэтому можно изобразить прямоугольную систему координат так,
чтобы точка
взаимно
перпендикулярны. Поэтому можно изобразить прямоугольную систему координат так,
чтобы точка  совпадала
с точкой начала координат.
совпадала
с точкой начала координат.

Тогда зная длины рёбер  ,
,
 и
и
 не
трудно отметить единичные отрезки и определить координаты всех вершин.
не
трудно отметить единичные отрезки и определить координаты всех вершин.
Мы с вами будем находить синус угла между прямой и каждой из данных плоскостей.
Сначала разберёмся с прямой. Она проходит через
середины рёбер  и
и
 ,
пусть это будут точки
,
пусть это будут точки  и
и
 .
И для вычисления синуса угла нужно знать координаты направляющего вектора. В
качестве направляющего вектора можно взять вектор
.
И для вычисления синуса угла нужно знать координаты направляющего вектора. В
качестве направляющего вектора можно взять вектор  .
.
Координаты точки  найдём
как координаты середины отрезка
найдём
как координаты середины отрезка  .
Каждая из них равна полусумме соответствующих координат точек
.
Каждая из них равна полусумме соответствующих координат точек  и
и
 .
Так получаем,
.
Так получаем,
 ,
,  .
.
Аналогично найдём координаты точки  ,
как полусумму соответствующих координат точек
,
как полусумму соответствующих координат точек  и
и
 .
Получаем
.
Получаем  ,
,  .
.
Теперь можем найти координаты вектора  как
разности соответствующих координат.
как
разности соответствующих координат.
Получаем, что направляющий вектор данной прямой
имеет координаты  .
.
Также для вычисления синуса угла между прямой и плоскостью необходимо знать координаты нормального вектора к плоскости, то есть перпендикулярного к ней.


Задача:
Доказать, что угол между скрещивающимися прямыми, одна из которых содержит
диагональ куба, а другая — диагональ грани куба, равен  .
.
Решение: изобразим прямоугольную координатную плоскость так, чтобы координатные оси совпадали с рёбрами куба.

Обозначим буквами вершины куба, через которые проходят
данные скрещивающиеся прямые. Найдём угол между прямыми  .
.
Пусть длина единичных отрезков на осях равна длине ребра куба.
Тогда в такой системе координат нетрудно найти координаты точек О, О1, О2 и О3.

А теперь найдём координаты векторов ОО1 и О2О3, которые являются направляющими для данных прямых.
Вектор  .
А вектор
.
А вектор  .
.
Найдём косинус угла между данными прямыми, подставив в формулу координаты направляющих векторов.
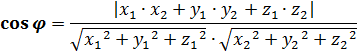
В ходе вычислений получаем, что

А значит, угол между прямыми  .
.
Что и требовалось доказать.
Итоги:
На этом уроке мы получили формулу вычисления косинуса угла между прямыми по координатам их направляющих векторов. А также формулу вычисления синуса угла между прямой и плоскостью по координатам направляющего вектора данной прямой и нормального вектора данной плоскости.

 Получите свидетельство
Получите свидетельство Вход
Вход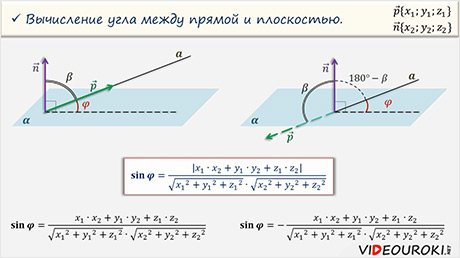



 0
0 22656
22656