Скалярное произведение векторов

Вы уже знакомы с понятием угла между векторами в пространстве. Поэтому на этом уроке мы приступим к рассмотрению скалярного произведения векторов в пространстве.

Как и на плоскости, скалярное произведение двух векторов в пространстве равно произведению длин этих векторов на косинус угла между ними.

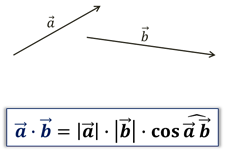
Задание: по рисунку определить величину угла между векторами.

Рассмотрим куб АBCDА₁B₁C₁D₁, сторона которого равна a, а точка О₁ — центр грани А₁B₁C₁D₁.

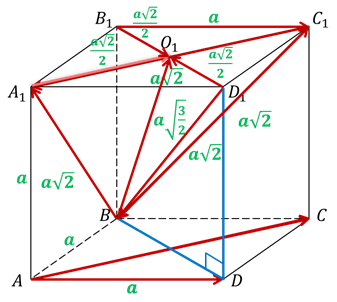
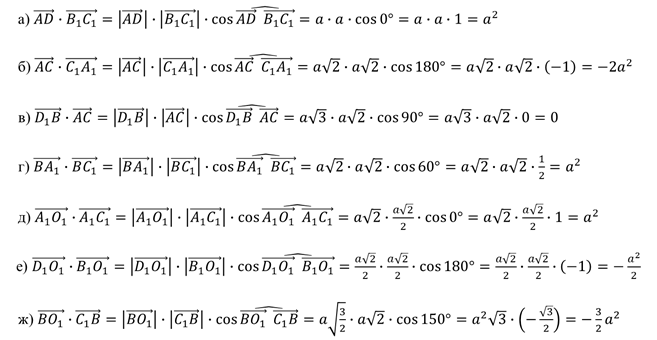
Мы с вами выполнили задание, где нашли скалярное произведение данных пар векторов.

Можно заметить, что, если угол между векторами острый, то скалярное произведение больше нуля. А если угол между векторами тупой, то их скалярное произведение меньше нуля. И только лишь когда векторы перпендикулярны, их скалярное произведение равно нулю. В данном случае, конечно, имеется в виду, что рассматриваемые векторы ненулевые.

А сейчас попробуем разобраться, как находить скалярное произведение векторов по их координатам.

На плоскости скалярное произведение двух векторов равнялось сумме произведений соответствующих координат. В пространстве имеет место такая же формула.

Задание: по координатам векторов ,  и  найти значения выражений: , , , , .

Решение:

Задание: пользуясь координатами векторов , , , выяснить, каким является угол между парами векторов: острым, прямым или тупым.

а)                             б)                             в)

Решение:

Итак, мы узнали и использовали 2 формулы скалярного произведения.

Выразив из первой формулы косинус угла между векторами, скалярное произведение можно расписать по второй формуле. А вот длины векторов запишем как корни квадратные из сумм квадратов их соответствующих координат.

Так мы получили формулу вычисления косинуса угла между векторами по их координатам.

Задание: найти угол между векторами  и .

а) , , б) , , в) , , г) , , д) , .

Решение:

Стоит отметить, что для скалярного произведения векторов в пространстве справедливы те же свойства, что и для скалярного произведения на плоскости.

Скалярный квадрат вектора всегда больше либо равен нулю.

; , если

А также можно записать переместительный, распределительный и сочетательный законы скалярного произведения. Они позволят в будущем преобразовывать выражения с векторами.

 (переместительный закон)

 (распределительный закон)

 (сочетательный закон)

Итоги:

На этом уроке мы сформулировали определение скалярного произведения двух векторов в пространстве, записали формулу вычисления скалярного произведения векторов по их координатам и получили формулу вычисления косинуса угла между двумя векторами. Помимо этого, для скалярного произведения в пространстве имеют место те же свойства, что и на плоскости.