Ранее мы с вами рассматривали угол между двумя векторами на плоскости.

Если от точки О отложить векторы ОА и ОВ, равные
векторам  и
и
 ,
соответственно, тогда угол АОВ будет являться углом между векторами
,
соответственно, тогда угол АОВ будет являться углом между векторами  и
и
 .
.
Обозначим градусную меру угла АОВ за  .
Говорят, что угол между векторами А и В равен
.
Говорят, что угол между векторами А и В равен  .
Причём величина
.
Причём величина  не
зависит от выбора точки, от которой будут отложены векторы.
не
зависит от выбора точки, от которой будут отложены векторы.
Обозначают угол между векторами таким образом:  .
То есть знак угла будем ставят над векторами.
.
То есть знак угла будем ставят над векторами.
Примеры:

На этом уроке поговорим об углах между векторами в пространстве. Но стоит отметить, что два вектора пространства могут лежать на пересекающихся и параллельных прямых, а могут лежать на скрещивающихся прямых.

Если они лежат на пересекающихся или параллельных прямых, то через эти векторы можно провести плоскость. Это, впрочем, касается и векторов, лежащих на одной прямой.
Если же векторы лежат на скрещивающихся прямых, то через один из них можно провести плоскость параллельную второму вектору. А в этой плоскости не трудно изобразить ему равный. Угол между полученными векторами равен углу между данными векторами.
Получается, что вопрос угла между векторами в пространстве всё равно рассматривается в пределах плоскости. И всё, что вы раннее знали о таких углах из планиметрии справедливо и для пространства.
Стоит напомнить важное отличие угла между векторами
от угла между прямыми. Оно заключается в том, что величина угла между прямыми
изменяется в пределах  .
А угол между векторами —
.
А угол между векторами —  .
.
Вспомним частные случаи угла между векторами.
Первой рассмотрим пару сонаправленных векторов.

Видим, что угол между ними равен нулю.
Также угол между векторами равен нулю, если один из них является нулевым или оба вектора нулевые.

Ведь нулевой вектор сонаправлен любому, а значит, эти случаи можно отнести к первому, где рассматривались сонаправленные векторы.
Теперь рассмотрим пару противоположно направленных векторов, отложенных от одной точки.
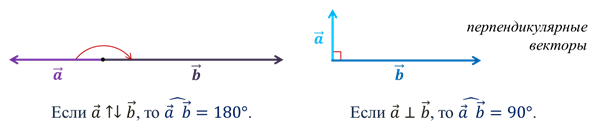
Видим, что угол между ними равен ста восьмидесяти градусам.
Ещё одним частным случаем являются векторы, угол между которыми равен 90о. Такие векторы называют перпендикулярными.
Повторив всё об углах между векторами, можем приступить к решению задач по этой теме.
Задание: рассмотрим куб АBCDА1B1C1D1. Найдём углы между данными векторами.
Решение:

Задание:
известно, что величина угла между векторами АB
и CD равна  .
Найдите величины углов между векторами ВА и DC,
BА и CD,
АB и DC.
.
Найдите величины углов между векторами ВА и DC,
BА и CD,
АB и DC.
Решение:

Итоги:
Повторив понятие угла между векторами на плоскости, мы выяснили, что все знания из планиметрии по данной теме справедливы и для пространства. А именно, что изменяется угол между векторами в пределах от нуля до ста восьмидесяти градусов. Причём его величина не зависит от выбора точки, от которой будут отложены векторы.
И имеют место следующие частные случаи.
Угол между сонаправленными векторами. Он равен нулю. Так же нулю равен угол между векторами, если хотя бы один из них является нулевым вектором.
Угол между противоположно направленными векторами равен 180о.
Ну, а если угол между векторами равен 90о, то такие векторы называют перпендикулярными.

 Получите свидетельство
Получите свидетельство Вход
Вход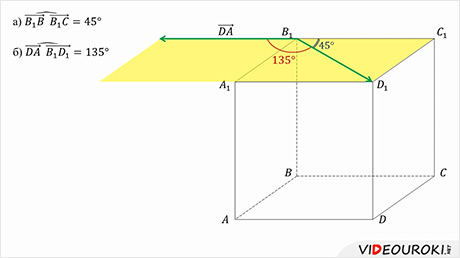



 0
0 5619
5619

