Простейшие задачи в координатах

Сегодня вы познакомитесь с формулами вычисления координат середины отрезка, вычисления длины отрезка по его координатам и вычисления расстояния между двумя точками.

Такие же задачи вы уже решали на плоскости. Сейчас же рассмотрим их в пространстве.

Итак, первым рассмотрим правило вычисления координат середины отрезка.

Отметим в прямоугольной координатной плоскости Охуz точку А с координатами x₁, y₁ и z₁, а также точку B с координатами x₂, y₂ и z₂. Отметим точку C, которая является серединой отрезка АB.

Можно записать, что вектор .

Действительно, ведь с одной стороны по правилу треугольника , а с другой стороны .

Сложим покомпонентно эти равенства. Справа видим сумму противоположных векторов , она равна нулю. Отсюда получаем, что вектор .

Векторы ОА и ОB являются радиус-векторами точек А и B соответственно. Отсюда запишем их координаты.

Равенство, выражающее вектор ОC через векторы ОА и ОB, запишем в координатах.

Получим такие координаты для вектора C. Но так как он является радиус-вектором точки C, то очевидно, что точка С будет иметь такие же координаты.

Можем сделать вывод, что каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Задание: точка М середина отрезка АВ. Найти координаты точки М по координатам точек А и В.

Решение:

Мы рассмотрели примеры применения формул координат середины отрезка, а теперь перейдём к следующему виду задач: вычисление длины вектора по его координатам.

Длина вектора  равна корню квадратному из суммы квадратов его координат.

Докажем это утверждение.

Что и требовалось доказать.

Задание: по координатам точек А и В найти длину вектора АВ.

а) , ;

б) , .

Решение:

Задание: Вычислить длины векторов , , ,  и .

Решение:

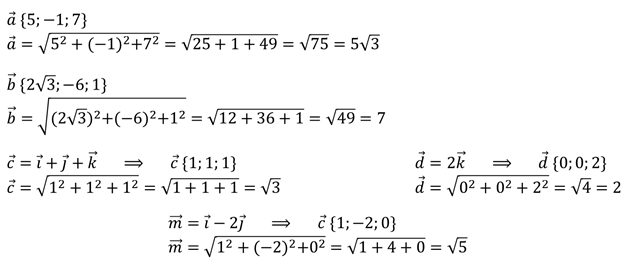
Далее рассмотрим ещё одну простейшую задачу в координатах: определение расстояния между двумя точками.

Отметим две произвольные точки пространства М₁ и М₂. Пусть координаты точки М₁ , а координаты точки М₂ .

Отрезок М₁М₂ и является расстоянием между этими точками. А ещё он является длиной вектора М₁М₂. А длину вектора мы умеем находить по его координатам.

Но для начала выразим координаты вектора через координаты его начала и конца.

Теперь выразим длину вектора М₁М₂, как корень квадратный из суммы квадратов его координат.

Таким образом, мы выразили длину отрезка М₁М₂ через координаты его концов и получили формулу вычисления расстояния между двумя точками с известными координатами.

Задание: По координатам точек ,  и  определить вид .

а) , , ;   б) , ,

Решение:

Зная координаты вершин треугольника, мы можем вычислить длины всех его сторон.

При выполнении этого задания мы применили формулу вычисления расстояния между двумя точками.

Задача: Найти расстояние от точки начала координат  до середины отрезка , если  и .

Решение:

Итоги:

На этом уроке вы познакомились с простейшими задачами в координатах. А именно: определением координат середины отрезка, вычислением длины отрезка по его координатам и расстояния между двумя точками.