Связь между координатами векторов и координатами точек

Вы уже знаете, как связаны координаты вектора с координатами точек на плоскости.

Вектор, конец которого совпадает с данной точкой, а начало — с точкой начала координат, называется радиус-вектором. И на плоскости координаты любой точки равны соответствующим координатам её радиус-вектора.

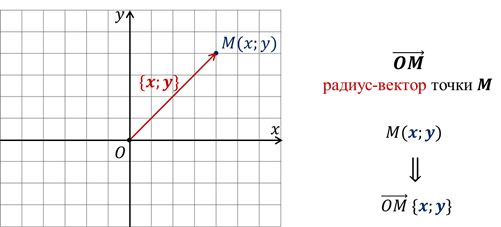
Это же утверждение справедливо и для пространства.

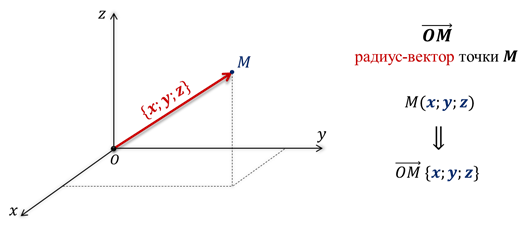
Определение:

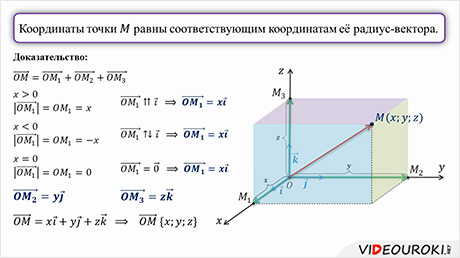
Вектор ОМ является радиус-вектором точки М пространства. И координаты любой точки пространства равны соответствующим координатам её радиус-вектора.

Докажем, это утверждение.

Так, мы доказали, что координаты любой точки пространства равны соответствующим координатам её радиус-вектора.

Теперь выразим координаты произвольного вектора пространства АВ через координаты его начала и конца.

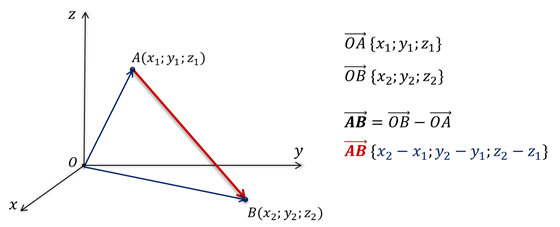
Пусть координаты начала А равны х₁, у₁ и z₁. А координаты конца B равны x₂, y₂ и z₂. Проведём радиус-векторы точек А и B. Понятно, что координаты вектора ОА равны соответствующим координатам точки А. А координаты вектора ОB равны координатам точки B.

Пользуясь правилом построения вектора разности двух векторов, можем отметить, что вектор АB равен разности векторов ОB и ОА. Почему ОB минус ОА, а не наоборот? Потому, что вектор разности направлен из конца вектора вычитаемого к концу вектора уменьшаемого. Значит, вектор ОB является уменьшаемым, а вектор ОА — вычитаемым.

Координаты векторов ОА и ОB известны. Тогда найдём координаты вектора АВ, как разности соответствующих координат векторов ОВ и ОА. Получаем, {𝑥₂−𝑥₁; 𝑦₂−𝑦₁; 𝑧₂−𝑧₁}. Так мы выразили координаты вектора через координаты его начала и конца.

Можно сделать вывод, что каждая координата вектора равна разности соответствующих координат его конца и начала.

Задание: по координатам точек 𝐴(2;−3;0), 𝐵(7;−12;18) и 𝐶(−8;0;5) определить координаты векторов 𝑂𝐴, 𝑂𝐵, 𝑂𝐶, 𝐴𝐵, 𝐵𝐶 и 𝐴𝐶, если точка 𝑂 — точка начала координат.

Решение:

Задание: По координатам векторов 𝑂𝐴{4;−7;1}, 𝑂𝐵{−2;0;3}, 𝑂𝐶{0,5;−4;8}, 𝐴𝐷{13;−2;5}, 𝐵𝐸{1;−3;0} и 𝐶𝐹{−9;0;0} определить координаты точек 𝐴, 𝐵, 𝐶, 𝐷, 𝐸 и 𝐹, если точка 𝑂 — точка начала координат.

Решение:

Мы рассмотрели примеры применения связи координат вектора и координат его начала и конца.

А сейчас поговорим о коллинеарных векторах.

Вы помните, если векторы А и В коллинеарны, то один можно выразить через другой умножением на некоторое число k. Причём, если , то векторы А и B сонаправлены, если же , то векторы А и B противоположно направлены.

Если координаты вектора , то координаты вектора .

Запишем отношения соответствующих координат данных векторов.

Все они равны между собой и равны k.

Так можно отметить, что если координаты векторов пропорциональны, то данные векторы коллинеарны.

Задание: по координатам векторов определить коллинеарны ли пары векторов.

Решение:

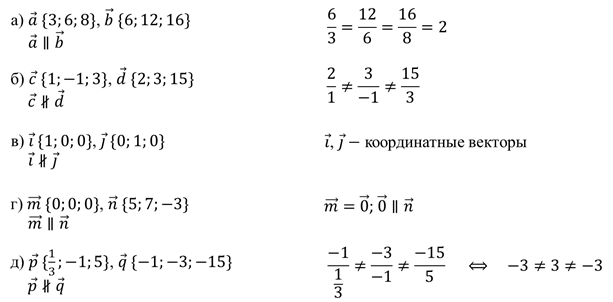
Задание: найти значения переменных m и n, при которых данные векторы будут коллинеарны.

Решение:

Вам также уже хорошо известно понятие компланарных векторов. Возникает вопрос, возможно, ли по координатам векторов определить компланарны они или нет?

Напомним, что компланарными называют векторы, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Другими словами, векторы компланарны, если имеются равные им векторы, лежащие в одной плоскости.

Так же мы выяснили, что любые два вектора всегда компланарны, а вот три вектора могут быть как компланарными, так и не компланарными.

В связи с этим мы доказали признак компланарности векторов.

Если вектор  можно разложить по векторам  и :  , то векторы ,  и компланарны.

Справедливо также и обратное утверждение, которое называют свойством компланарных векторов.

Если векторы ,  и компланарны (), то вектор  можно разложить по векторам  и :  , причём коэффициенты разложения определяются единственным образом.

Задание: рассмотрим тройки векторов с известными координатами и выясним компланарны они или нет.

Решение:

Итоги:

Вы узнали, что радиус-вектором точки в пространстве называется вектор, конец которого совпадает с данной точкой, а начало — с точкой начала координат. Координаты любой точки равны соответствующим координатам её радиус-вектора.

Мы с вами доказали, что каждая координата вектора равна разности соответствующих координат его конца и начала. А также, пользуясь тем, что любой вектор можно выразить через коллинеарный ему вектор, мы отметили, что если координаты векторов пропорциональны, то данные векторы коллинеарны. Также мы рассмотрели примеры определения компланарности векторов по их координатам.