Вспомним, как мы находили координаты вектора на плоскости.
Пользуясь тем, что любой вектор можно разложить по двум неколлинеарным векторам, на осях мы задавали единичные векторы. Таким образом, любой вектор можно разложить по данным единичным векторам, а координатами вектора являются коэффициенты этого разложения.
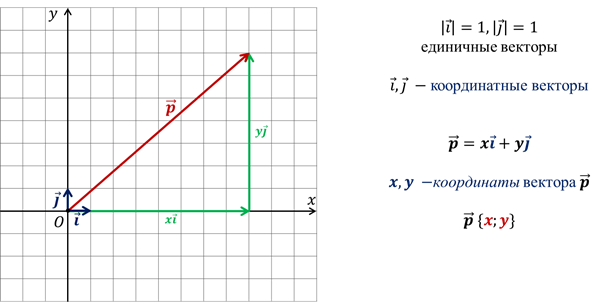
Так же вам уже известно, что любой вектор пространства можно выразить через 3 некомпланарных вектора, то есть векторы, не лежащие в одной плоскости.
Изобразим прямоугольную систему координат Охуz. На каждой из положительных осей от начала координат отложим единичные векторы.
Буквой i обозначим единичный вектор оси Оx, буквой j — единичный вектор оси Оy, буквой k — единичный вектор оси Оz.
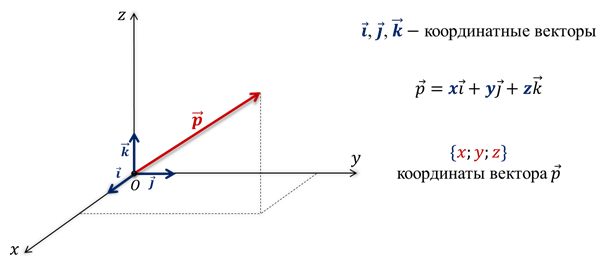
Определение:
Векторы i, j, k будем называть координатными векторами.
Понятно, что они являются некомпланарными. И поэтому любой вектор пространства можно разложить по единичным векторам i, j, k. Причём коэффициенты разложения х, у и z определяются единственным образом.
Коэффициенты х, у и z называют координатами вектора р в данной системе координат. Координаты вектора будем записывать в фигурных скобках в последовательности х, у, z.
Задание: Пользуясь разложениями векторов по координатным векторам, записать их координаты.
Решение:

Задание: пользуясь координатами векторов, запишем их разложения по координатным векторам i, j, k.
Решение:

Задача: В прямоугольном параллелепипеде 𝑂𝐴 = 2, 𝑂𝐵 = 3, а ОО1 = 2. Найти координаты векторов 𝑂𝐴1, 𝑂𝐵1, 𝑂𝑂1, 𝑂𝐶, 𝑂𝐶1, 𝐵𝐶1, 𝐴𝐶1 и 𝑂1 𝐶.
Решение:

После выполнения этого задания можно сделать вывод о том, что если вектор лежит в некоторой из координатных плоскостей или параллелен ей, а также лежит или параллелен некоторой из координатных осей, то его соответствующие координаты равны нулю.
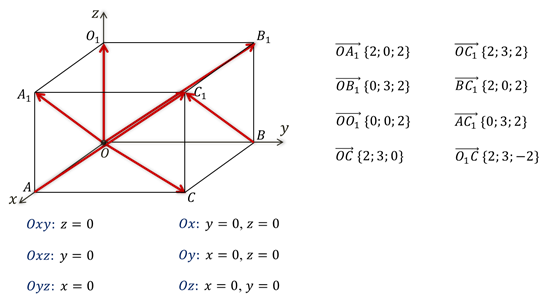
Если вектор лежит в координатной плоскости Оху или параллелен ей, то его аппликата равна нулю. Если вектор принадлежит или параллелен координатной плоскости Охz, то его ордината равна нулю. Если же вектор принадлежит или параллелен координатной плоскости Оyz, то его абсцисса равна нулю.
В случае, когда вектор лежит на оси координат Оx или параллелен ей, то ордината и аппликата равны нулю. Если вектор принадлежит или параллелен оси Оy, то абсцисса и аппликата равны нулю. И если вектор принадлежит или параллелен оси Оz, то абсцисса и ордината равны нулю.
А сейчас поговорим о противоположных векторах. Из планиметрии известно, что координаты противоположных векторов противоположны. Это утверждение верно и для векторов в пространстве.
Задание: найти координаты векторов противоположных данным векторам.
Решение:

Также из курса планиметрии вам известны правила определения координат вектора суммы, вектора разности и произведения вектора на число.

Такие же правила действую и для координат векторов в пространстве.

Задание: 𝑎 ⃗{−1;0;3}, 𝑏 ⃗{5;−2;1} и 𝑐 ⃗{1;7;−2}. Определить координаты векторов:
1) 𝑎 ⃗+𝑐 ⃗; 2) 𝑏 ⃗−𝑎 ⃗; 3) 2𝑎 ⃗+𝑏 ⃗; 4) 1/2 𝑎 ⃗−2𝑏 ⃗+𝑐 ⃗.
Решение:

Так, используя правила определения координат вектора суммы, разности и произведения вектора на число, мы определили координаты данных векторов.
Итоги:
Сегодня мы ввели понятие координатных векторов i, j, k. И, пользуясь тем, что любой вектор пространства можно выразить через 3 некомпланарных вектора, записали, что коэффициенты х, у и z называют координатами вектора p в данной системе координат.
Мы отметили, что все координаты нулевого вектора равны нулю. Равные векторы имеют равные координаты, а координаты противоположных векторов противоположны.
Также мы записали правила, которые позволяют находить координаты любого вектора, представленного в виде алгебраической суммы данных векторов, координаты которых известны.

 Получите свидетельство
Получите свидетельство Вход
Вход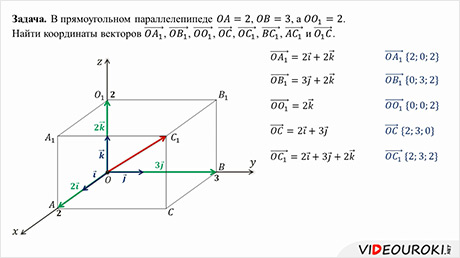



 0
0 17146
17146

