Л.р.№1 Исследование РУД без начальной скорости

Цель лабораторной работы — исследовать закономерности равноускоренного движения без начальной скорости и определить ускорение движения тела, а также его мгновенную скорость в конце движения.

Впервые данную лабораторную работу проводил Галилео Галилей. Именно благодаря данной работе Галилею удалось установить опытным путём ускорение свободного падения.

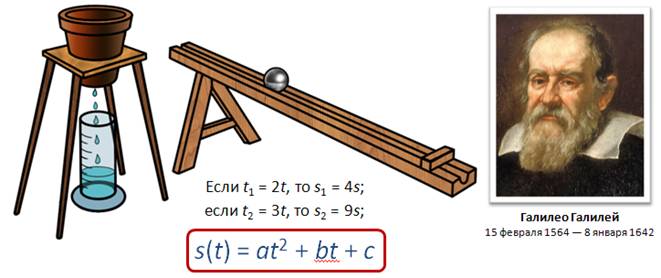
Задача: рассмотреть и разобрать, как можно определить ускорение тела при его движении по наклонному жёлобу.

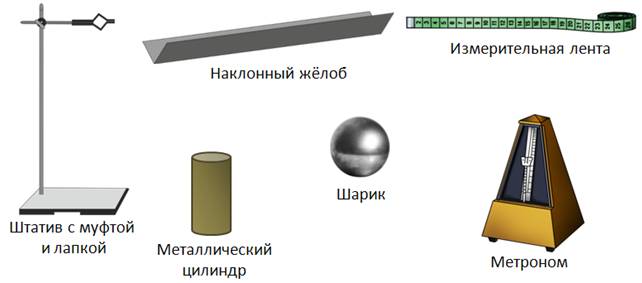
Оборудование: штатив с муфтой и лапкой, наклонный жёлоб; упор в виде металлического цилиндра. Движущееся тело — это шарик. Счётчик времени — метроном. Измерительная лента понадобится для измерения расстояния.

Известно, что шарик скатывается по прямолинейному наклонному желобу равноускорено.

При равноускоренном движении без начальной скорости пройденное расстояние определяется по формуле:

Откуда

Зная ускорение, можно определить мгновенную скорость по формуле:

Если измерить промежуток времени от начала движения шарика до его остановки при ударе о цилиндр и расстояние, пройденное им за это время, то по формуле (2) мы вычислим ускорение шарика, а по формуле (3) — его мгновенную скорость.

Промежуток времени измеряется с помощью метронома.

Метроном настраивают на 120 ударов в минуту, значит, промежуток времени между двумя следующими друг за другом ударами будет равен 0,5 секунды.

Удар метронома, одновременно с которым шарик начинает движение, считается нулевым.

В нижней половине желоба помещают цилиндр для торможения шарика. Положение цилиндра опытным путем подбирают так, чтобы удар шарика о цилиндр совпадал с третьим или четвертым от начала движения ударом метронома. Тогда время движения можно вычислить по формуле:

где n — число ударов метронома, не считая нулевого удара (или число промежутков времени по 0,5 секунды от начала движения шарика до его остановки).

Начальное положение шарика отмечается мелом. Расстояние s, пройденное им до остановки, измеряют сантиметровой лентой.

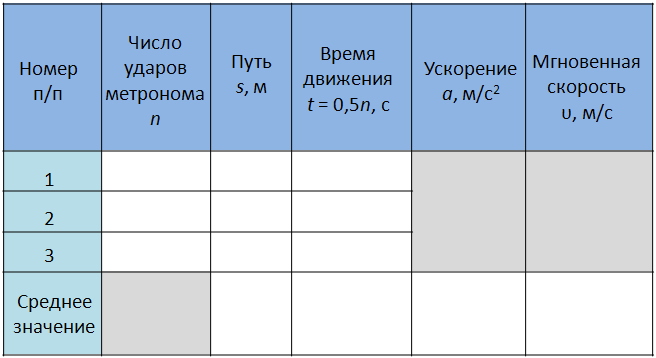
Составим таблицу, состоящую из шести столбцов, каждый из которых необходимо заполнить.

Порядок выполнения работы.

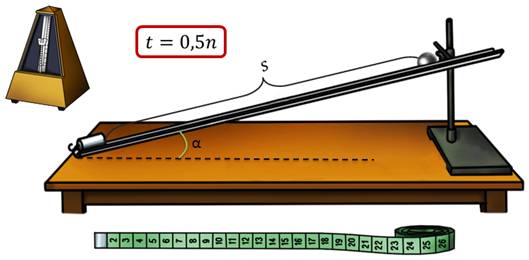
1. Укрепите желоб с помощью штатива в наклонном положении под небольшим углом к горизонту. У нижнего конца желоба положите в него металлический цилиндр.

2. Пустив шарик (одновременно с ударом метронома) с верхнего конца желоба, подсчитайте число ударов метронома до столкновения шарика с цилиндром.

3. Меняя угол наклона желоба к горизонту и, производя небольшие передвижения металлического цилиндра, добивайтесь того, чтобы между моментом пуска шарика и моментом его столкновения с цилиндром было 4 удара метронома (3 промежутка между ударами).

4. По формуле (4) вычислите время движения шарика.

5. С помощью измерительной ленты определите длину перемещения шарика.

Не меняя наклона желоба (условия опыта должны оставаться неизменными), повторите опыт еще три раза, добиваясь снова совпадения четвертого удара метронома с ударом шарика о металлический цилиндр (цилиндр для этого можно немного передвигать).

6. По формуле

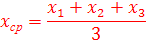
найдите среднее значение модуля перемещения и промежутка времени, а затем рассчитайте среднее значение модуля ускорения по формуле (2), подставляя в нее найденные средние значения пройденного пути и времени.

По формуле (3) рассчитайте среднее значение модуля мгновенной скорости тела.

7. Результаты измерений и вычислений занесите в таблицу.

8. Вычисляем погрешности измерений.

Приборные погрешности определяем по паспорту прибора.

Для измерительной ленты:

Δs = ± 0,005 м.

Для промежутка времени:

Δt = 1 c.

Вычисляем абсолютные погрешности каждого из измерений.

Для этого сначала вычисляем модули абсолютных погрешностей каждого отдельного измерения по формулам:

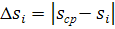
и

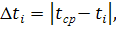
где i — это номер опыта.

Далее оцениваем абсолютную погрешность прямых измерений.

Вычисляем абсолютную и относительную погрешность косвенных измерений.

Относительную погрешность для ускорения рассчитаем по формуле:

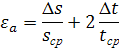
Тогда абсолютная погрешность для ускорения равна

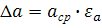
Результат записываем в интервальной форме.

Аналогичным способом находим погрешности в вычислениях и для мгновенной скорости тела.

Результат также записываем в интервальной форме.

Таким образом, выяснили, как можно определить ускорение движущегося тела.