В данной теме будет разобран общий алгоритм решения задач по кинематике.
Задача
1.
Два автомобиля движутся прямолинейно в одну сторону с постоянными скоростями 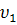 и
и
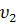 (причем
скорость первого автомобиля больше скорости второго), и в некоторый момент
времени расстояние между ними равно s.
Через какой промежуток времени и в каком месте первый автомобиль догонит
второй?
(причем
скорость первого автомобиля больше скорости второго), и в некоторый момент
времени расстояние между ними равно s.
Через какой промежуток времени и в каком месте первый автомобиль догонит
второй?
|
Дано:
|
Решение:
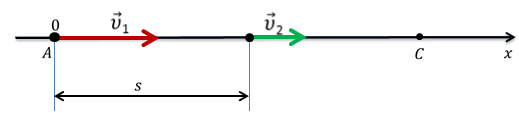
Обе материальные точки движутся равномерно и прямолинейно, следовательно, их движения описываются уравнениями движения:
Чтобы решить вопрос о последующем состоянии точек, надо знать их начальные условия, т.е. координаты и скорости в начальный момент времени. Т.к. автомобили движутся равномерно, то их начальная скорость совпадает со скоростями в любые последующие моменты и потому:
С учетом этого уравнения примут вид:
Эти уравнения справедливы для любого момента времени, для любой точки траектории (время — переменная величина, которая может принимать любые значения). Следовательно, они справедливы и для интересующего нас момента времени, когда первый автомобиль догонит второй. Когда один автомобиль догнал другой, означает, что в этот момент времени они находились в одной и той же точке пространства, т.е. их координаты были равны.
Запишем систему уравнений для данного момента времени
Решая полученную систему уравнений найдем искомые величины.
|
|
|
Алгоритм решения кинематических задач:
1) выбрать систему отсчета (это предполагает выбор тела отсчета; начала системы координат; положительного направления осей; момента времени, принимаемого за начальный).
2) определить вид движения вдоль каждой из осей и написать кинематические уравнения движения вдоль каждой оси — уравнения для координаты и скорости. Если тел несколько, то уравнения пишутся для каждого тела.
3) определить начальные условия (координаты и проекции скорости в начальный момент времени), а также проекции ускорения (если в условии задачи говорится о равноускоренном движении) и подставить эти величины в уравнения движения.
4) определить дополнительные условия, т.е. координаты или скорости для каких-либо моментов времени (или точек траектории), и написать уравнения движения для выбранных моментов времени (т.е. подставить эти значения координат и скорости в уравнения движения).
5) полученную систему уравнений решить относительно искомых величин.
Задача 2. Катер, двигаясь против течения реки, проплывает около стоящего на якоре буя и встречает там плот. Через 15 мин после встречи катер повернул обратно и догнал плот на расстоянии 1200 метров ниже буя. Найти скорость течения реки.
|
Дано:
|
СИ
|
Решение: 1 способ:
Согласно закону сложения скоростей
где
Вверх по течению
Вниз по реке
Запишем уравнения движения тел
Для момента, когда катер догонит плот (точка А), имеем
2 способ: Систему отсчета свяжем с плотом. Тогда уравнения движения будут иметь вид.
Для точки А имеем
Решая полученное линейное уравнение, находим скорость течения реки. |
|
|
Ответ: скорость течения реки 0,7 м/с.
Дополнения к алгоритму решения задач по кинематике:
1. Систему отсчета не обязательно связывать с неподвижным телом. В ряде случаев задача решается проще, если система отсчета связана с движущимся телом.
2. Систему отсчета надо выбирать так, чтобы наиболее простым образом можно было определить начальные условия.
3. При выборе системы отсчета надо четко установить, какая точка принимается за начало осей координат и какой момент времени за начальный.
4. Не забывайте проверять размерность величин, стоящих в левой и правой частях уравнения.

 Получите свидетельство
Получите свидетельство Вход
Вход





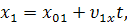
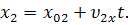









 Пусть:
Пусть: –
скорость плота, относительно буя;
–
скорость плота, относительно буя; –
скорость
катера, относительно буя.
–
скорость
катера, относительно буя.
 –
скорость катера относительно плота (течения реки).
–
скорость катера относительно плота (течения реки).



 Ответ:
скорость течения реки 0,7 м/с.
Ответ:
скорость течения реки 0,7 м/с.


 0
0 11826
11826

