Напомним,
что степенной функцией называется функция вида  ,
где
,
где  —
заданное действительное число. Вы уже знакомы с частными случаями степенных
функций, когда
—
заданное действительное число. Вы уже знакомы с частными случаями степенных
функций, когда  является
натуральным или целым числом, например, с такими функциями, как
является
натуральным или целым числом, например, с такими функциями, как  ,
,
 ,
,
 ,
,
 ….
….
Давайте вспомним, как выглядят графики этих функций.
Итак,
если  ,
то есть имеем функцию
,
то есть имеем функцию 
Графиком этой функции будет прямая, проходящая через начало координат.

Если
 —
чётное число (
—
чётное число ( ),
то графиком функции является парабола.
),
то графиком функции является парабола.

Графиком
функции  ,
при нечётном
,
при нечётном  (
( ),
является кубическая парабола.
),
является кубическая парабола.

Если
 , то
, то  .
Графиком этой функции является гипербола.
.
Графиком этой функции является гипербола.

Свойства
степенной функции напрямую зависят от свойств степени с
действительным показателем и в частности от того, при каких значениях  и
и
 имеет
смысл
имеет
смысл  .
.
Давайте рассмотрим некоторые свойствами функций, которыми обладают, в частности, отдельные степенные функции.
Итак,
функция  ,
определённая на множестве
,
определённая на множестве  большое,
называется ограниченной снизу на множестве
большое,
называется ограниченной снизу на множестве  ,
если существует число
,
если существует число  такое,
что для любого
такое,
что для любого  выполняется
неравенство
выполняется
неравенство  .
.
Как
же это понимать? Это означает, что все точки графика ограниченной снизу функции ,
где
,
где  ,
расположены выше прямой игрек равно
,
расположены выше прямой игрек равно  или
на этой прямой.
или
на этой прямой.

Функция ,
определённая на множестве
,
определённая на множестве  большое,
называется ограниченной сверху на множестве
большое,
называется ограниченной сверху на множестве  большое,
если существует число
большое,
если существует число такое,
что для любого
такое,
что для любого  ,
выполняется неравенство
,
выполняется неравенство  .
.
В
этом случае все точки графика функции  ,
где
,
где  ,
лежат ниже прямой игрек равно
,
лежат ниже прямой игрек равно  или
на этой прямой.
или
на этой прямой.

Например:
Функция
 является
ограниченной снизу, так как
является
ограниченной снизу, так как  .
То есть парабола ограничена снизу прямой
.
То есть парабола ограничена снизу прямой  .
.

А
функция  ограничена
сверху, так как
ограничена
сверху, так как  ,
то есть парабола ограничена сверху прямой
,
то есть парабола ограничена сверху прямой  .
.

Функцию, ограниченную и сверху, и снизу на множестве икс большое, называют ограниченной на этом множестве.
Функция
 является
ограниченной на множестве
является
ограниченной на множестве  тогда
и только тогда, когда существует положительное число
тогда
и только тогда, когда существует положительное число  такое,
что для любого большое
такое,
что для любого большое ,
выполняется неравенство
,
выполняется неравенство  .
.

Ещё
вам нужно знать, что если существует такое значение  из
области определения множества
из
области определения множества  функции
функции
 ‚
что для любого
‚
что для любого из
этой области справедливо неравенство
из
этой области справедливо неравенство  ,
то говорят, что функция
,
то говорят, что функция  принимает
наименьшее значение
принимает
наименьшее значение  при
при
 .
.
Например,
функция  принимает
при
принимает
при  наименьшее
значение, равное
наименьшее
значение, равное  .
.

Если
же существует такое значение  из
области определения множества
из
области определения множества  функции
функции
 ,
что для любого
,
что для любого  справедливо
неравенство
справедливо
неравенство  ,
то говорят,
,
то говорят,  принимает
наибольшее значение
принимает
наибольшее значение  при
при
 ..
..
Например,
функция  принимает
при
принимает
при  наибольшее
значение, равное 5.
наибольшее
значение, равное 5.

А
теперь давайте более подробно рассмотрим свойства степенной функции
в зависимости от показателя степени  .
.
Случай
1. Показатель  —
чётное натуральное число.
—
чётное натуральное число.
В
этом случае степенная функция  ,
где
,
где  —
натуральное число, обладает следующими свойствами:
—
натуральное число, обладает следующими свойствами:
—
область определения — все действительные числа, то есть множество действительных
чисел  ;
;
—
множество значений — неотрицательные числа, то есть  ;
;
—
функция  чётная,
так как
чётная,
так как  ;
;
—
функция является убывающей на промежутке  и
возрастающей на промежутке
и
возрастающей на промежутке  ;
;
—
функция ограничена снизу, так как  для
любого
для
любого  ;
;
—
функция принимает наименьшее значение  при
при
 .
.
График
функции  имеет
такой же вид, как, например, график функции
имеет
такой же вид, как, например, график функции  ,
или
,
или  и
так далее. График этой функции называют параболой n-й степени.
и
так далее. График этой функции называют параболой n-й степени.

Случай
2. Показатель  —
нечётное натуральное число.
—
нечётное натуральное число.
В
этом случае степенная функция ,
где
,
где —
натуральное число, обладает следующими свойствами:
—
натуральное число, обладает следующими свойствами:
— область определения — множество действительных чисел;
— множество значений — множество действительных чисел;
—
функция  нечётная,
так как
нечётная,
так как  ;
;
— функция является возрастающей на всей действительной оси;
— функция не является ограниченной ни сверху, ни снизу;
— функция не принимает ни наибольшего, ни наименьшего значения.
График
функции имеет
такой же вид, как, например, график функции
имеет
такой же вид, как, например, график функции  .
График этой функции называют кубической параболой.
.
График этой функции называют кубической параболой.

Случай
3. Показатель  ,
где
,
где —
натуральное число.
—
натуральное число.
В
этом случае степенная функция ,
обладает следующими свойствами:
,
обладает следующими свойствами:
—
область определения — множество действительных чисел, кроме  ;
;
—
множество значений — положительные числа  ;
;
—
функция  ,
чётная, так как
,
чётная, так как  ;
;
—
функция является возрастающей на промежутке  и
убывающей на промежутке
и
убывающей на промежутке  ;
;
—
функция ограничена снизу, так как  ;
;
— функция не принимает ни наибольшего, ни наименьшего значения.
График
функции имеет такой же вид, как, например, график функции  .
.

Прямую
 (ось
абсцисс) называют горизонтальной асимптотой (от греческого слова asymptotes,
что переводится как «несовпадающий») графика функции
(ось
абсцисс) называют горизонтальной асимптотой (от греческого слова asymptotes,
что переводится как «несовпадающий») графика функции  ,
при
,
при  .
Прямую
.
Прямую  (ось
ординат) называют вертикальной асимптотой графика этой функции
(ось
ординат) называют вертикальной асимптотой графика этой функции ,
так как при значениях
,
так как при значениях  ,
близких к
,
близких к  ,
расстояния от точек этого графика до оси
,
расстояния от точек этого графика до оси  (прямой
(прямой )
становятся сколь угодно малыми.
)
становятся сколь угодно малыми.
Случай
4. Показатель  ,
где
,
где  —
натуральное число.
—
натуральное число.
В
этом случае степенная функция  ,
где
,
где ,
обладает следующими свойствами:
,
обладает следующими свойствами:
—
область определения — множество действительных чисел, кроме  ;
;
—
множество значений — множество действительных чисел, кроме  ;
;
—
функция  ,
нечётная, так как как
,
нечётная, так как как  ;
;
—
функция является убывающей на промежутках  и
и
 ;
;
— функция не является ограниченной;
— функция не принимает ни наибольшего, ни наименьшего значения.
График
функции ,
имеет такой же вид, как, например, график функции
,
имеет такой же вид, как, например, график функции  .
.

Ось абсцисс является горизонтальной асимптотой, а ось ординат — вертикальной асимптотой графика функции.
Случай
5. Показатель  —
положительное действительное нецелое число.
—
положительное действительное нецелое число.
В
этом случае функция  обладает
следующими свойствами:
обладает
следующими свойствами:
—
область определения — множество неотрицательных чисел  ;
;
—
множество значений — множество неотрицательных чисел  ;
;
—
функция является возрастающей на промежутке  ;
;
— функция не является ни чётной, ни нечётной;
—
функция ограничена снизу, так как  ;
;
—
функция принимает наименьшее значение  при
при
 .
.
График
функции  ,
где
,
где  —
положительное нецелое число, имеет такой же вид, как, например, график функции
—
положительное нецелое число, имеет такой же вид, как, например, график функции  (при
(при
 )
или как, например, график функции
)
или как, например, график функции  (при
(при
 ).
).


Случай
6. Показатель  —
отрицательное действительное нецелое число.
—
отрицательное действительное нецелое число.
В
этом случае функция  обладает
следующими свойствами:
обладает
следующими свойствами:
—
область определения — множество положительных чисел  ;
;
—
множество значений — множество положительных чисел  ;
;
—
функция является убывающей на промежутке  ;
;
— функция не является ни чётной, ни нечётной;
—
функция ограничена снизу, так как  .
.
График
функции  ,
где
,
где  —
отрицательное нецелое число, имеет такой же вид, как, например, график функции
—
отрицательное нецелое число, имеет такой же вид, как, например, график функции  .
.


 Получите свидетельство
Получите свидетельство Вход
Вход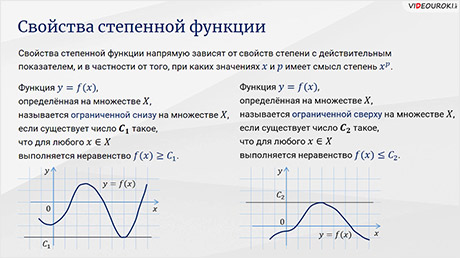



 0
0 45277
45277

