Вопросы занятия:
· дадим определение скрещивающихся прямых;
· рассмотрим возможные случаи взаимного расположения двух прямых в пространстве;
· докажем теорему, которая выражает признак скрещивающихся прямых
· докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.
Материал урока.
Для начала давайте вспомним определение параллельных прямых в пространстве. Итак, две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Давайте рассмотрим все тот же наш любимый куб ABCDA1B1C1D1.
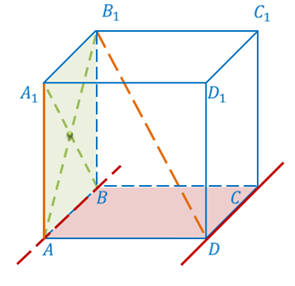
Понятно, что прямые, на которых лежат его ребра AB и DC параллельны, ведь они лежат в одной плоскости, например, ABC и не пересекаются.
Проведем диагонали AB1A1B грани AA1B1B. Видно, что прямые на которых лежат указанные диагонали расположены в одной плоскости AA1B1 и пересекаются.
Теперь давайте проведем диагональ куба B1D. И попытаемся разобраться о взаимном расположении прямых, на которых лежат диагональ B1D и ребро AA1. Обратите внимание, что нет такой плоскости, которая проходила бы через обе эти прямые. Значит, параллельными они быть не могут, по определению параллельности прямых в пространстве. Пересекаться также не могут, так как не лежат в одной плоскости.
Для такого случая расположения прямых также есть название. Такие прямые называют скрещивающимися.
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
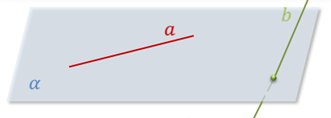
На
экране изображены скрещивающиеся прямые а и b.
Их обозначают следующим образом 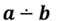 .
.
Итак, возможны три случая взаимного расположения двух прямых в пространстве:
1. прямые пересекаются, т.е. имеют одну только общую точку.
2. прямые параллельны, т.е. лежат в одной плоскости и не пересекаются.
3. прямые скрещивающиеся, т.е. не лежат в одной плоскости, не параллельны и не пересекаются.

Наглядным примером о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая – под эстакадой.
Линии электропередач и река. Они также дают нам представление о скрещивающихся прямых.
Докажем теорему, которая позволяет выяснить, являются ли две прямые скрещивающимися. Эту теорему называют признаком скрещивающихся прямых.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Доказательство. Пусть прямая а лежит в плоскости α, а прямая b пересекает эту плоскость в точке М, не лежащей на прямой а. Докажем, что прямые а и b скрещиваются, т.е. не существует плоскость, в которой они обе лежат.
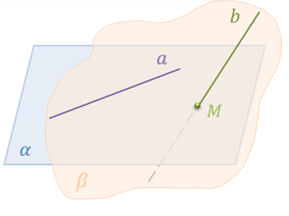
Предположим, что прямые а и b лежат в некоторой плоскости β. Тогда плоскость β проходит через прямую а и точку М, а следовательно, совпадает с плоскостью α (так как через прямую и не лежащую на ней точку проходит единственная плоскость).
Получили, что прямая b лежит в плоскости α, а это противоречит условию теоремы.
Таким образом, наше предположение неверно, а значит, прямые а и b – скрещивающиеся.
Теорема доказана.
Рассмотрим пример. Пусть ABCA1B1C1 – прямая треугольная призма.
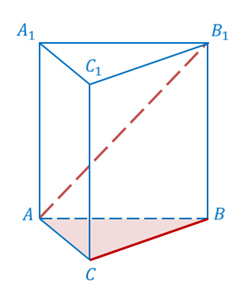
Тогда прямые AB1 и BC – скрещивающиеся, так как прямая AB1 пересекает плоскость ABC в точке А, не лежащей на прямой BC.
Задача.
Точки
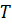 и
и
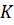 лежат
на ребре
лежат
на ребре 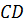 ,
а точки
,
а точки 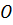 и
и
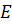 на
ребре
на
ребре 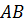 тетраэдра
тетраэдра
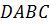 .
Докажите, что прямые
.
Докажите, что прямые 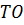 и
и
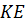 –
скрещивающиеся.
–
скрещивающиеся.
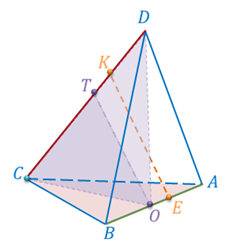
Доказательство. Прямая ТК пересекает плоскость ABC в точке C, не лежащей на прямой ОЕ, следовательно, прямые ТК и ОЕ скрещивающиеся. Значит, точки Т, К, Е и О не лежат в одной плоскости. Обратите внимание, прямая ТО лежит в плоскости ТОC. КЕ пересекает плоскость ТОC в точке К. Точка К не принадлежит прямой ТО. Отсюда следует, что прямые ТО и КЕ не лежат в одной плоскости, т.е. по признаку скрещивающихся прямых они являются скрещивающимися. Что и требовалось доказать.
Докажем еще одну теорему о скрещивающихся прямых.
Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство. Пусть а и b скрещивающиеся прямые. Докажем, что через прямую b проходит плоскость, параллельная прямой а. Через какую-либо точку М прямой b проведем прямую c, параллельную прямой а.
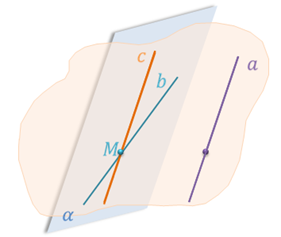
Пусть α– плоскость, проходящая через прямые b и c. Так как прямая а не лежит в плоскости α и параллельна прямой c, лежащей в этой плоскости, то прямая а параллельна плоскости α.
Понятно, что плоскость α – единственная плоскость, проходящая через прямую b и параллельная прямой а. Действительно, любая другая плоскость, проходящая через прямую b, пересекается с прямой c, а следовательно, пересекается и с параллельной ей прямой а. Теорема доказана.
Наглядным примером этой теоремы служат две дороги, одна из которых проходит по эстакаде, а другая – под эстакадой. Нижняя дорога лежит в плоскости земли, параллельной дороге на эстакаде. Ясно, что и через дорогу на эстакаде проходит плоскость, параллельная плоскости земли, а значит, параллельная нижней дороге.
Задача. Точки 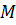 и
и 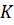 – центры граней куба. Докажите, что прямые
– центры граней куба. Докажите, что прямые 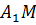 и
и 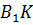 скрещиваются
скрещиваются
Доказательство.
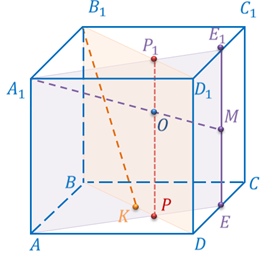

Что и требовалось доказать.
Подведем итоги урока. На этом уроке мы дали определение скрещивающихся прямых. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Рассмотрели три возможных случая взаимного расположения двух прямых в пространстве. Доказали теорему, которая выражает признак скрещивающихся прямых. А также доказали теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 21738
21738

