Углы с сонаправленными сторонами

Вопросы занятия:

·     введем понятие сонаправленных лучей;

·     дадим определение сонаправленных лучей;

·     докажем теорему о равенстве углов с сонаправленными сторонами.

Материал урока.

На этом уроке нам понадобится одна из аксиом планиметрии, которая звучит следующим образом: «любая прямая разбивает плоскость на две полуплоскости».

Итак, пусть у нас есть некоторая прямая а, которая лежит в плоскости α. Согласно аксиоме, эта прямая разделяет плоскость α на две части. Каждую из которой, называют полуплоскостью.

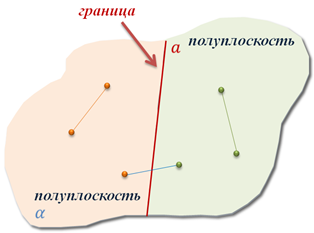
Понятно, что наша прямая а разделила плоскость α на две полуплоскости. Одна из которых лежит слева от прямой а, вторая – справа. В свою очередь, прямую а называют границей каждой из этих полуплоскостей.

Обратите внимание, любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а. А вот любые две точки разных полуплоскостей лежат по разные стороны от этой прямой.

Определение. Два луча ОА и О₁А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО₁.

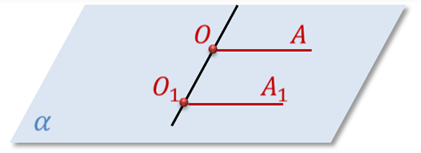
Напомню, что два луча называются параллельными, если они лежат на параллельных прямых.

Лучи ОА и O₁A₁, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Докажем теорему об углах с сонаправленными сторонами.

Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

Доказательство. Рассмотрим случай, когда углы О и О₁ с соответственно сонаправленными сторонами лежат в разных плоскостях.

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные лучи ОB и

О₁B₁. Т.е. мы имеем два угла АОB и А₁О₁B₁, стороны которых лежат на сонаправленных лучах. Докажем, что угол АОB равен углу А₁О₁B₁.

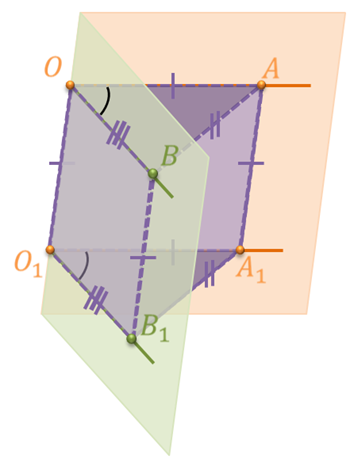
Отметим на сторонах лучей ОА и O₁A₁ точки А и A₁ так, чтобы отрезки ОА и O₁A₁ были равны. На сторонах лучей ОB и O₁B₁ отметим точки B и B₁ так, чтобы отрезки ОB и O₁B₁ были равны.

Рассмотрим четырехугольник ОАA₁O₁. Так как лучи ОА и O₁A₁ параллельны по условию (сонаправленны ) и равны по построению, то четырехугольник ОАА₁О₁ является параллелограммом по признаку параллелограмма. Следовательно, АА₁ параллельно ОО₁ и АА₁ равно ОО₁.

Рассмотрим четырехугольник ОBB₁O₁. Его стороны ОB и O₁B₁ параллельны, т.к. лежат на сонаправленных лучах по условию и равны по построению. Значит, по признаку параллелограмма четырехугольник OBB₁O₁ является параллелограммом. Тогда, стороны BB₁ и OO₁ параллельны и равны.  

Обратите внимание, мы получили, что прямая AA₁ параллельна прямой OO₁ и прямая BB₁ параллельна прямой OO₁. Тогда по признаку параллельности прямых в пространстве, прямые AA₁ и BB₁ параллельны.

Рассмотрим четырехугольник BAA1B1. В этом четырехугольнике стороны AA₁ и BB₁ параллельны и равны. А значит, BAA₁B₁ – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A₁B₁ тоже параллельны и равны.

Теперь рассмотрим треугольники АОB и A₁O₁B₁. Стороны ОА и O₁A₁ равны по построению. Стороны ОB и O₁B₁ также равны по построению. Выше мы доказали, что стороны АB и A₁B₁ равны. Значит, треугольники АОB и A₁O₁B₁ равны по трем сторонам. Напомню, что в равных треугольниках против соответственно равных сторон лежат равные углы. Значит, углы АОB и A₁O₁B₁ равны. Теорема доказана.

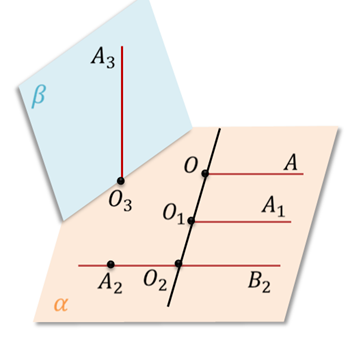
Задание. Рассмотрите рисунок и 

а) укажите лучи, которые являются сонаправленными;

б) укажите лучи, которые не являются сонаправленными.

Решение.

Подведем итоги урока. На этом уроке мы ввели понятие сонаправленных лучей. Узнали, что два луча ОА и О один А один в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей О О один. Лучи ОА и О один А один, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой. А также доказали теорему о равенстве углов с сонаправленными сторонами.