Угол между прямыми

Вопросы занятия:

·     рассмотрим углы между пересекающимися и скрещивающимися прямыми в пространстве.

Материал урока.

Напомню, что два луча ОА и O₁A₁ в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей ОO₁. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

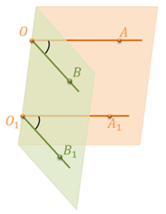
Как вы уже знаете, любые две пересекающиеся прямые лежат в одной плоскости и образуют четыре неразвернутых угла. Если известен один из этих углов, то можно найти и другие три угла.

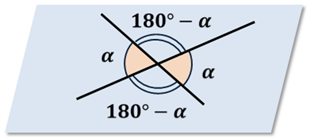
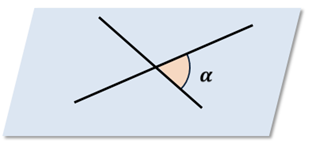
Определение. Если пересекающиеся прямые образуют тупые и острые углы, то углом между этими прямыми называется тот, который не превосходит любой из трех остальных углов, т.е. наименьший из углов.

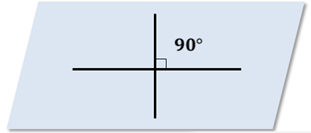
Если пересекающиеся прямые образуют четыре равных угла, то угол между этими прямыми равен девяносто градусов.

Пусть α – тот из углов, который не превосходит любого из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен α. Очевидно, что угол альфа между двумя пересекающимися прямыми удовлетворяет условию: .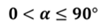

Теперь введем понятие угла между скрещивающимися прямыми. Пусть нам даны две скрещивающиеся прямые а и b. Возьмем произвольную точку М₁ в пространстве и проведем через нее прямые A₁B₁, параллельные прямым а и b соответственно.

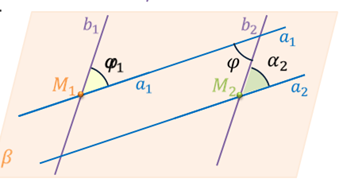
Тогда углом между скрещивающимися прямыми а и b называется угол между построенными пересекающимися прямыми A₁B₁. Т. е. если угол между прямыми A₁B₁ равен φ, то будем говорить, что угол между скрещивающимися прямыми а и b равен φ.

Докажем, что угол между скрещивающимися прямыми не зависит от выбора точки М₁.

Возьмем любую другую точку М₂ и проведем через нее прямые a₂ и b₂, параллельные прямым а и b соответственно. Пусть угол между прямыми a₁ и b₁ равен α₁, а угол между прямыми a₂ и b₂ равен α₂.

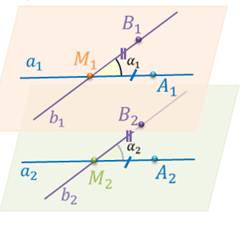
Если прямые a₁, b₁, a₂, b₂ лежат в одной плоскости, то по свойству накрест лежащих углов при параллельных прямых угол α₁ равен углу φ и равен углу α₂.

Пусть теперь прямые a₁ и b₁, пересекающиеся в точке М₁, лежат в одной плоскости. А прямые a₂ и b₂, пересекающиеся в точке М₂ лежат в другой плоскости.

Так как прямая a₁ параллельна прямой а и прямая a₂ параллельна прямой а, то по признаку параллельности прямых в пространстве прямые a₁ и a₂ также параллельны. Так как прямая b₁ параллельна прямой b и прямая b₂ параллельна прямой b, то по признаку параллельности прямых в пространстве прямые b₁ и b₂ параллельны.

Отметим на прямых a₁ и a₂ точки A₁ и A₂ так, чтобы отрезки М₁А₁ и М₂А₂ были равны. На прямых b₁ и b₂ отметим точки B₁ и B₂ так, чтобы отрезки M₁B₁и M₂B₂ были равны.

Угол A₁M₁B₁ равен углу α₁, угол A₂M₂B₂ равен α₂.

Тогда стороны угла A₁M₁B₁ и угла A₂M₂B₂ попарно сонаправлены. По теореме о равенстве углов с сонаправленными сторонами получаем, что угол A₁M₁B₁ равен углу A₂M₂B₂. Т. е. имеем, что угол α₁ равен углу α₂.

Таким образом, величина угла между скрещивающимися прямыми не зависит от выбора точки M₁.

Замечание. Угол между параллельными прямыми в пространстве считается равным 0º.

Рассмотрим пример. Пусть у нас есть треугольная пирамида DABC. На ее ребре DB взята точка Т.

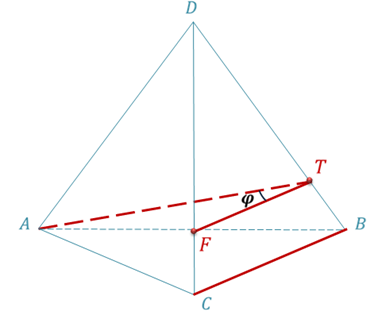
Тогда угол между скрещивающимися прямыми BC и АТ равен углу между прямой АТ и прямой TF, которая проходит через точку Т параллельно прямой BC в плоскости BDC.

Рассмотрим еще пример. Пусть есть параллелепипед ABCDA₁B₁C₁D₁. И пусть точка О – точка пересечения диагоналей грани A₁B₁C₁D₁, а точка F – точка пересечения диагоналей грани AA₁B₁B.

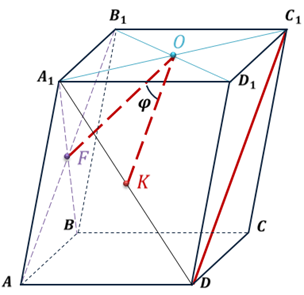
Тогда угол между скрещивающимися прямыми C₁D и OF равен углу между прямыми OF и прямой OK, проходящей через точку О и параллельной прямой C₁D в плоскости C₁DA₁.

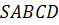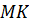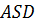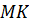Задача. Дана правильная пирамида .  – средняя линия грани . Найдите угол между прямыми  и .

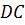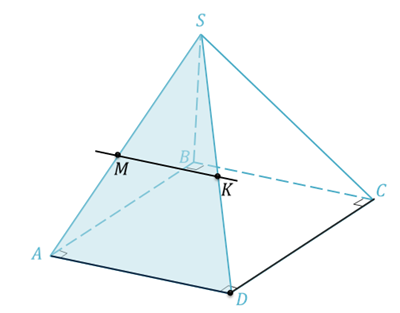
Решение.

Запишем ответ: 90º

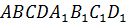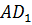Задача. Дан куб . Найдите угол между прямыми  и .

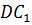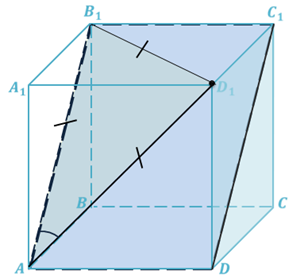
Решение.

Ответ: 60º.

Подведем итоги урока. На этом уроке мы рассмотрели углы между пересекающимися и скрещивающимися прямыми. А также решили несколько задач на нахождение скрещивающихся углов.