Видеоучебник / Физика / Решение задач по физике. Механика 7-11 класс. / Движение тела, брошенного горизонтально

Новогодняя распродажа готовых материалов для учителей! Скидки до 50 %

Движение тела, брошенного горизонтально

Урок 7. Решение задач по физике. Механика 7-11 класс.

На этом занятии мы решим три задачи по данной теме. Выведем основные расчетные формулы, связанные с ней. Научимся их применять для решения конкретных типов задач. Рассмотрим характеристики такого движения в произвольный момент времени.

Конспект урока "Движение тела, брошенного горизонтально"

«Конечно, обдумывай «что»,

но еще больше обдумывай «как»!»

Иоганн Гёте

В данной будем разбираться с движением тела, брошенным горизонтально.

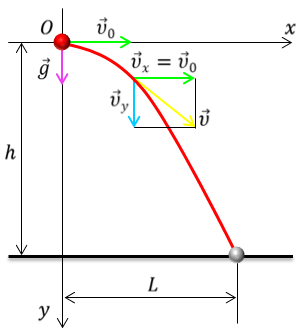
Задача 1. При прыжке в воду с десятиметровой вышки спортсмен, отталкиваясь ногами, приобретает скорость 2 м/с, направленную горизонтально. Определите время, через которое спортсмен достигнет поверхности воды, его дальность полета и модуль скорости в момент входа в воду. Сопротивление воздуха не учитывать.

ДАНО:

РЕШЕНИЕ:

При t = 0:

Запишем кинематические уравнения РУД и РПД, а также уравнения проекций скоростей:

Или, с учетом начальных условий:

В момент достижения поверхности воды:

Тогда

Скорость спортсмена в любой момент времени найдем по теореме Пифагора:

Тогда его скорость у поверхности воды:

Таким образом, искомые величины могут быть определены по формулам

Данные формулы являются одними из основных формул при решении задач на движение тела, брошенного горизонтально.

Ответ: t₁ = 1,4 c; L = 2,8 м; υ₁ = 14,3 м/с.

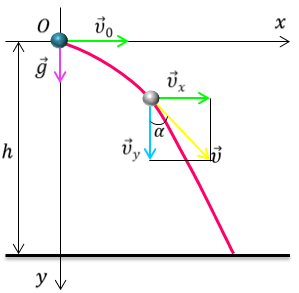
Задача 2. С башни бросили небольшое ядро в горизонтальном направлении со скоростью 48 км/ч. Определите модуль скорости и угол, который образует вектор скорости с вертикалью через 1400 мс. Сопротивление воздуха пренебрежимо мало.

ДАНО:

СИ

РЕШЕНИЕ:

Скорость ядра в любой момент времени:

Ответ: υ = 19,3 м/с; α = 43,6^о.

Задача 3. Пикирующий бомбардировщик времен ВОВ Пе-2 заходит на цель поду углом 60^о к горизонту на скорости 125 м/c и сбрасывает бомбу на высоте 500 м. На каком расстоянии от цели в горизонтальном направлении летчик должен освободить бомбу, чтобы она поразила цель? Сопротивлением воздуха пренебречь.

ДАНО: