Вопросы занятия:
· рассмотреть задачи на движение по прямой;
· рассмотреть задачи на движение по воде;
· задачи на движение протяжённых тел;
· задачи на движение по замкнутой трассе.
Материал урока
Прежде чем мы приступим к решению ключевых задач давайте вспомним основную формулу, которая описывает движение.

В математике при решении задач считается, что тела двигаются прямолинейно и равномерно, скорости постоянны в течение определённых промежутков времени. Скорости не меняются при поворотах. Движущиеся тела считаются материальными точками, не имеющими размеров и массы, если в условии задании не указаны размеры тела.
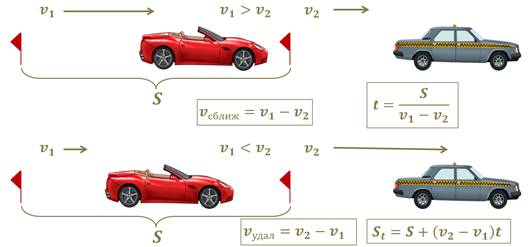
Теперь давайте рассмотрим возможные виды движения двух тел по прямой.
Движение навстречу друг другу.
Если тела движутся навстречу друг другу, то скорость их сближения равна сумме скоростей данных тел.

Следующим мы рассмотрим движение тел в противоположные стороны.
Если два тела движутся в противоположные стороны, то скорость их удаления друг от друга равна сумме скоростей этих тел.

Теперь давайте рассмотрим задачи на движение в одном направлении.
Рассмотрим задачу.
Задача.

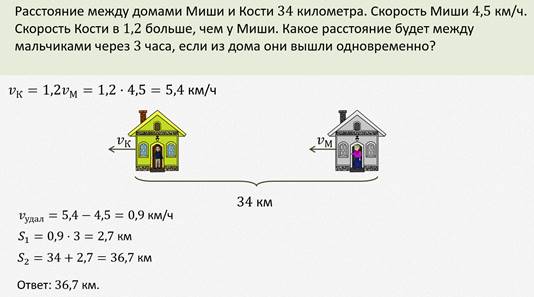
Давайте решим ещё несколько задач.
Задача.

Задача.
Следующий тип задач, которые мы рассмотрим – задачи на движение по воде.
При решении задач этого типа надо помнить следующее:
Если тело движется по течению реки, то скорость тела равна сумме собственной скорости тела (то есть скорости в стоячей воде) и скорости течения реки.
Если же тело движется против течения реки, то скорость тела равна разности собственной скорости тела и скорости течения реки.
Если же в условии говорится о движении плотов, то тогда скорость тела равна скорости реки (собственная скорость плота равна нулю).
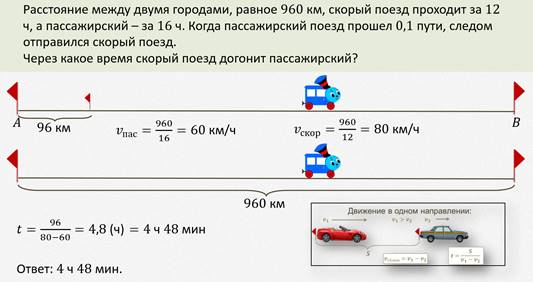
Рассмотрим задачу.
Задача.
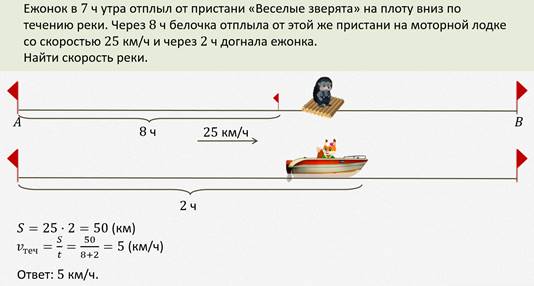
Рассмотрим ещё одну задачу.
Задача.

Теперь давайте рассмотрим задачи на движение протяжённых тел.
Как правило, в задачах на движение протяжённых тел требуется определить длину одного из тел. Ключевой задачей на движение протяжённых тел является задача, в которой надо определить длину поезда, который проезжает мимо столба или протяжённой платформы. В первом случае поезд проходит мимо столба расстояние, равное длине поезда. Во втором случае, пройденное расстояние равно сумме длин поезда и платформы.
Рассмотрим задачу.
Задача.
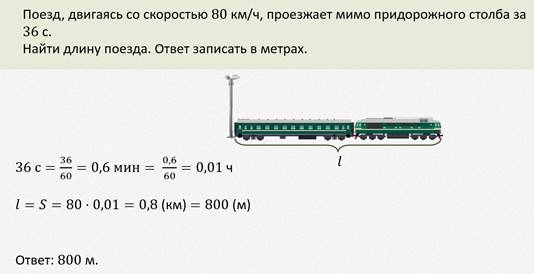
Рассмотрим ещё одну задачу.
Задача.
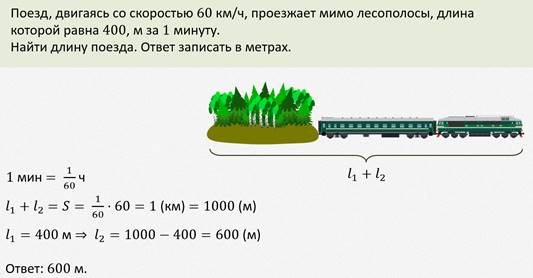
При решении задач на движение двух тел, удобно считать одно из тел – неподвижным, а второе – приближающимся к нему со скоростью равной сумме скоростей этих тел (если движение происходит навстречу) или разности скоростей, если движение происходит вдогонку. Такая модель позволяет лучше разобраться с условием задачи.
Рассмотрим задачу.
Задача.

Мы с вами рассмотрели только основные виды задач на движение. Но есть такие задачи, которые тоже на движение, но не принадлежат ни одному из перечисленных видов.
Рассмотрим пример.
Пример.

Итоги урока
Сегодня мы рассмотрели задачи на движение по прямой, на движение по воде, задачи на движение протяженных тел, а также рассмотрели задачу на движение по замкнутой трассе.


 Получите свидетельство
Получите свидетельство Вход
Вход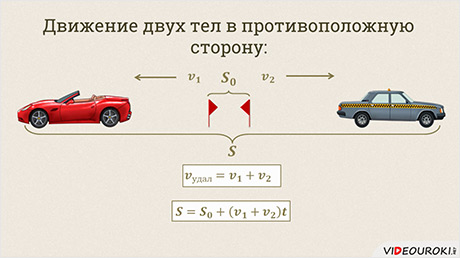



 0
0 5789
5789



