Четырехугольники. Основные элементы четырехугольников

Вопросы занятия:

·  вспомнить, какими свойствами обладают четырёхугольники;

·  назвать признаки соответствующих четырёхугольников;

·  рассмотреть решения некоторых задач по данной теме.

Материал урока

Прежде чем мы начнём говорить о конкретных четырёхугольниках, давайте вспомним, какая вообще фигура является четырёхугольником.

Вообще, многоугольник, который имеет четыре вершины, называют четырёхугольником.

Итак, четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.

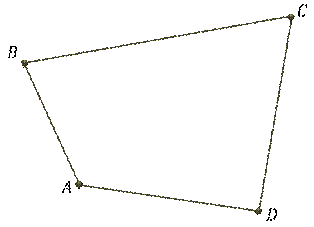
При этом никакие три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Давайте назовём основные элементы четырёхугольника.

Точки , ,  и  называются вершинами четырёхугольника.

Отрезки , ,  и , соединяющие эти точки, называются сторонами четырёхугольника.

Вершины четырёхугольника, принадлежащие одной стороне, называются соседними. Например, вершины  и ,  и  являются соседними.

Вершины, которые не являются соседними, называются противоположными. Так в нашем четырёхугольнике вершины  и ,  и  являются противоположными.

Стороны четырёхугольника, исходящие из одной вершины, называются соседними. Например, стороны  и  являются соседними.

Стороны, не имеющие общего конца, называются противоположными. Так стороны  и ,  и  являются противоположными.

Напомним, что четырёхугольники бывают выпуклыми и невыпуклыми.

Выпуклый четырёхугольник лежит по одну сторону от прямой, проходящей через любые две соседние вершины.

А вот если четырёхугольник лежит по разные стороны хотя бы от одной прямой, проходящей через две соседние вершины, то он является невыпуклым.

В дальнейшем будем говорить только о выпуклых четырёхугольниках.

Отрезки, соединяющие противоположные вершины четырёхугольника, называются диагоналями.

Так в четырёхугольнике  отрезки  и  являются диагоналями.

Каждая диагональ разделяет этот четырёхугольник на два треугольника. Вот, например, диагональ  разбивает четырёхугольник  на два треугольника  и . Поскольку сумма углов каждого треугольника равна 180^о, то сумма углов четырёхугольника равна 360^о.

Напомним ещё, что периметром четырёхугольника называется сумма длин всех его сторон.

А теперь перейдём к конкретным четырёхугольникам. И первым рассмотрим параллелограмм.

Определение.

Параллелограммом называют четырёхугольник, у которого противоположные стороны попарно параллельны.

Высотой параллелограмма называют перпендикуляр, проведённый из некоторой вершины на одну из противоположных сторон.

Вспомним какими свойствами обладает параллелограмм.

Первое свойство.

Сумма углов при соседних вершинах параллелограмма равна 180^о.

Докажем это свойство. Рассмотрим параллелограмм .

По определению параллелограмма стороны , то есть лежат на параллельных прямых. Прямая , которая проходит через две соседние вершины, является секущей. А тогда  и  – внутренние односторонние.

Нам известно, что если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180^о. Следовательно, .

А так как эти углы являются углами при соседних вершинах параллелограмма, то свойство доказано.

Второе свойство.

Диагональ разбивает параллелограмм на два равных треугольника.

Доказательство. Проведём в параллелограмме  диагональ . Получим два треугольника  и . У этих треугольников сторона  – общая, а прилежащие к ней углы , как накрест лежащие при параллельных прямых  и  и секущей , , как накрест лежащие при параллельных прямых  и  и секущей .

Таким образом, получаем, что треугольники  по стороне и двум прилежащим углам, то есть по второму признаку.

Что и требовалось доказать.

Третье свойство.

У параллелограмма противоположные стороны равны.

Доказательство. Рассмотрим параллелограмм . Диагональ  разделяет его на два треугольника:  и . Доказывая предыдущее свойство, мы выяснили, что , то есть у них соответствующие стороны равны. Т.е. сторона , .

Что и требовалось доказать.

Четвёртое свойство.

У параллелограмма противоположные углы равны.

Доказательство. Рассмотрим параллелограмм . Проведём диагональ .

, как накрест лежащие при параллельных прямых  и  и секущей , , как накрест лежащие при параллельных прямых  и  и секущей . Угол параллелограмма . . А так как , то, понятно, что .

Что и требовалось доказать.

Пятое свойство.

Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство. Рассмотрим параллелограмм . Пусть точка О – точка пересечения диагоналей  и .

Рассмотрим треугольники  и . Стороны , как противоположные стороны параллелограмма. , как накрест лежащие углы при пересечении параллельных прямых  и  секущей . Углы , как накрест лежащие при пересечении параллельных прямых  и  секущей .

А тогда треугольники  по второму признаку. Следовательно, у них соответствующие стороны равны. Поэтому , . То есть диагонали точкой пересечения делятся пополам.

Что и требовалось доказать.

Ещё стоит вспомнить признаки параллелограмма.

Первый признак.

Если у четырёхугольника две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Доказательство. Пусть в четырёхугольнике  стороны  и .

Проведём диагональ , которая разделяет наш четырёхугольник на 2 треугольника  и . Сторона  у этих треугольников общая. Стороны  по условию. , как накрест лежащие при параллельных прямых  и  и секущей .

Таким образом, получили, что треугольники  по двум сторонам и углу между ними, то есть по первому признаку. Из равенства треугольников следует, что .

Углы  являются накрест лежащими при пересечении прямых  и  секущей . А так как эти углы равны, то прямые .

Так мы получили, что в рассматриваемом четырёхугольнике  противоположные стороны попарно параллельны, а, следовательно, этот четырёхугольник – параллелограмм.

Что и требовалось доказать.

Второй признак.

Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм.

Доказательство. Пусть в четырёхугольнике  сторона , сторона .

Проведём диагональ , которая разделит четырёхугольник на 2 треугольника  и . Сторона  у этих треугольников – общая. Сторона  по условию. Сторона  также по условию. Получается, что рассматриваемые треугольники  по трём сторонам, то есть по третьему признаку. Отсюда следует, что .

А так как эти углы являются накрест лежащими при пересечении прямых  и  секущей , то .

Таким образом, мы получили, что противоположные стороны  и , а тогда по первому признаку четырёхугольник  – параллелограмм.

Что и требовалось доказать.

Третий признак.

Если у четырёхугольника диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.

Доказательство. Пусть в четырёхугольнике  диагонали  и делятся этой точкой пополам.

Рассмотрим треугольники  и . У них сторона  по условию, а сторона  также по условию. А  как вертикальные. Получаем, что треугольники  по первому признаку равенства треугольников.

Из равенства треугольников следует, что .

А так как углы  являются накрест лежащими при пересечении прямых  и  секущей , то .

Таким образом, получили, что в четырёхугольнике  стороны  и , а, следовательно, по первому признаку четырёхугольник является параллелограммом.

Что и требовалось доказать.

Вспомним определение прямоугольника.

Прямоугольник – это параллелограмм, у которого все углы прямые.

Так как прямоугольник является параллелограммом, то он обладает всеми его свойствами.

У прямоугольника противоположные стороны равны.

,

Диагонали прямоугольника точкой пересечения делятся пополам.

,

Кроме этих свойств рассмотрим ещё одно свойство – свойство диагоналей прямоугольника: диагонали прямоугольника равны.

Доказательство. Пусть  – прямоугольник. Проведём диагонали  и . И рассмотрим прямоугольные треугольники  и . У них катет  – общий, а катеты  как противоположные стороны прямоугольника.

Таким образом, прямоугольные треугольники  по двум катетам.

Из равенства треугольников следует, что , то есть диагонали прямоугольника  равны.

Что и требовалось доказать.

Верным будет и обратное утверждение, которое является признаком прямоугольника: если у параллелограмма диагонали равны, то этот параллелограмм – прямоугольник.

Вспомним определение ромба.

Ромб – это параллелограмм, у которого все стороны равны.

Так как ромб является параллелограммом, то он обладает всеми его свойствами, которые мы с вами уже вспомнили.

Кроме того, он обладает следующим свойством: диагонали ромба взаимно перпендикулярны и лежат на биссектрисах его углов.

Доказательство. Пусть  – ромб. Диагонали ромба . Рассмотрим треугольник .

Так как диагонали параллелограмма (а значит и ромба) точкой пересечения делятся пополам, то . Следовательно, отрезок  – медиана .

По определению у ромба все стороны равны, а значит, сторона .

Таким образом, получаем, что треугольник  является равнобедренным. А тогда медиана , проведённая к основанию, по свойству равнобедренного треугольника, является биссектрисой и высотой.

Следовательно, диагональ ромба  и лежит на биссектрисе угла .

Что и требовалось доказать.

Имеют место и обратные утверждения, являющиеся признаками ромба: если одна из диагоналей параллелограмма делит его углы пополам, то этот параллелограмм – ромб.

Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм – ромб.

Вспомним определение квадрата.

Квадрат – это прямоугольник, у которого все стороны равны.

Также можно сказать, что квадрат – это ромб, у которого все углы прямые.

Эти два определения равносильны. Из каждого следует, что квадрат – это параллелограмм, который одновременно является и прямоугольником, и ромбом. Следовательно, квадрат обладает всеми свойствами и прямоугольника, и ромба.

Основные свойства квадрата:

Все углы квадрата прямые.

Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и лежат на биссектрисах его углов.

И ещё нам стоит вспомнить определение трапеции.

Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны трапеции называются основаниями. А не параллельные – боковыми сторонами.

Перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение, называется высотой трапеции.

Отрезок, соединяющий середины боковых сторон, называют средней линией трапеции. Он параллелен основаниям, а длина его равна половине суммы оснований трапеции.

Трапеция, у которой есть прямой угол, называется прямоугольной.

Трапеция, у которой боковые стороны равны, называется равнобедренной.

Давайте вспомним некоторые свойства и признаки равнобедренной трапеции.

Первое свойство – это свойство углов равнобедренной трапеции: углы при основании равнобедренной трапеции равны.

Второе свойство – свойство диагоналей равнобедренной трапеции: диагонали равнобедренной трапеции равны.

И назовём признаки равнобедренной трапеции.

Первый признак: если у трапеции углы при основании равны, то она равнобедренная.

Второй признак: если у трапеции диагонали равны, то она равнобедренная.

Ну а теперь давайте рассмотрим решения некоторых задач по теме «четырёхугольники».

Задача.

Угол между двумя высотами параллелограмма, выходящими из вершины одного из его тупых углов, равен . Найдите углы параллелограмма.

Итак, пусть  – параллелограмм,  и  – его высоты, тогда  и .

Понятно, что угол .

Рассмотрим треугольник . Он прямоугольный, так как  – высота по условию. Значит, . Угол  мы уже вычислили, он равен . Так как сумма углов треугольника равна , то угол . А тогда в параллелограмме  угол , как противолежащие углы параллелограмма.

Угол  как углы параллелограмма, прилежащие к одной стороне.

Тогда угол , как противолежащие углы параллелограмма.

Задача.

Меньшая сторона прямоугольника равна  см; один из углов, получившихся при пересечении диагоналей, равен . Найдите длины диагоналей.

Пусть  – прямоугольник, у которого сторона  см, угол .

Тогда угол , по свойству смежных углов.

В треугольнике  сторона , также равна . Угол . Значит, треугольник  равносторонний и тогда  см.

А значит,  см.

Задача.

В равнобедренной трапеции высота, проведённая из вершины тупого угла, делит большее основание на отрезки в  см и  см. Определите основания этой трапеции.

Пусть  – трапеция, , ,  см,  см.

Тогда  – прямоугольник по построению. Следовательно, , .

Заметим, что треугольники  по гипотенузе и катету. А тогда  см.

 см.

 см,  см.

Итоги урока

На этом уроке мы говорили о четырёхугольниках. Вспомнили, какими свойствами они обладают. Назвали признаки соответствующих четырёхугольников. А затем рассмотрели решения некоторых задач по данной теме.