Вопросы занятия:
· вспомнить признаки параллельных прямых;
· рассмотреть решения некоторых задач по теме «параллельные прямые».
Материал урока
Начнём с определения параллельных прямых.
Две прямые  и
и  называются параллельными,
если они не пересекаются.
называются параллельными,
если они не пересекаются.

Обозначают это так  .
.
Прямая  называется секущей
в отношении прямых
называется секущей
в отношении прямых  и
и  , если она
пересекает каждую из них в разных точках.
, если она
пересекает каждую из них в разных точках.

При пересечении прямых  и
и  секущей
секущей  образуются
образуются  углов.
углов.
На экране каждый из углов обозначен соответствующей цифрой. Напомним, что некоторые пары этих углов носят специальные названия:
·
 и
и  ,
,  и
и  – называют внутренними
накрест лежащими углами;
– называют внутренними
накрест лежащими углами;
·
 и
и  ,
,  и
и  – внешние
накрест лежащие углы;
– внешние
накрест лежащие углы;
·
 и
и  ,
,  и
и  ,
,  и
и  ,
,  и
и  – соответственные
углы;
– соответственные
углы;
·
 и
и  ,
,  и
и  – внутренние
односторонние углы;
– внутренние
односторонние углы;
·
 и
и  ,
,  и
и  – внешние
односторонние углы.
– внешние
односторонние углы.
А теперь давайте вспомним признаки параллельности прямых.
Первый признак параллельности прямых.
Если при пересечении двух прямых  и
и  секущей
секущей  накрест лежащие
углы равны, то прямые параллельны.
накрест лежащие
углы равны, то прямые параллельны.

Докажем признак. Допустим
противное. Пусть при пересечении двух прямых  и
и  третьей
третьей  накрест лежащие
углы
накрест лежащие
углы  , но прямые
пересекаются в некоторой точке М.
, но прямые
пересекаются в некоторой точке М.
Давайте отложим на прямой  отрезок
отрезок  , и соединим точки А
и
, и соединим точки А
и  . Рассмотрим
треугольники
. Рассмотрим
треугольники  и
и
 . У них стороны
. У них стороны  по построению,
сторона
по построению,
сторона  – общая, а угол
– общая, а угол  по условию. Значит,
по условию. Значит,
 по двум сторонам и
углу между ними.
по двум сторонам и
углу между ними.
Из равенства треугольников  следует, что
следует, что  .
.
Так как углы  и
и  смежные, то их
сумма равна 180о. А тогда и сумма углов
смежные, то их
сумма равна 180о. А тогда и сумма углов  и
и  тоже равна 180о.
Следовательно, точки
тоже равна 180о.
Следовательно, точки  ,
,  и
и  лежат на одной
прямой. Но ведь этого быть не может. Значит, наше предположение неверно. Тогда
прямые
лежат на одной
прямой. Но ведь этого быть не может. Значит, наше предположение неверно. Тогда
прямые  .
.
Что и требовалось доказать.
Второй признак параллельности прямых.
Если при пересечении двух прямых  и
и  секущей
секущей  соответственные
углы равны, то прямые параллельны.
соответственные
углы равны, то прямые параллельны.

Доказательство. Пусть при
пересечении двух прямых  и
и  секущей
секущей
 два соответственных
угла, например,
два соответственных
угла, например,  .
.
Углы  , как вертикальные.
, как вертикальные.
Из равенств углов  ,
,  следует, что
следует, что  . Но ведь углы
. Но ведь углы  и
и  накрест лежащие. А
значит, по первому признаку параллельности прямых прямые
накрест лежащие. А
значит, по первому признаку параллельности прямых прямые  .
.
Что и требовалось доказать.
Третий признак параллельности прямых.
Если при пересечении двух прямых
секущей сумма односторонних углов равна  , то прямые
параллельны.
, то прямые
параллельны.

Доказательство. Пусть при
пересечении прямых  и
и
 секущей
секущей
 сумма односторонних
углов равна 180о. Например, угол
сумма односторонних
углов равна 180о. Например, угол  .
.
Так как углы  и
и  смежные, то их
сумма равна
смежные, то их
сумма равна  .
.
Из первого и второго равенств
следует, что  . В свою очередь
углы
. В свою очередь
углы  и
и  накрест лежащие,
следовательно, по первому признаку параллельности прямых, прямые
накрест лежащие,
следовательно, по первому признаку параллельности прямых, прямые  .
.
Что и требовалось доказать.
Кстати, верными будут и утверждения, обратные этим признакам. Их называют свойствами углов, образованных при пересечении двух параллельных прямых секущей.
Вспомним их:
если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна сто восемьдесят градусов.

И вспомним ещё четвёртый признак параллельности прямых.
Если две прямые  и
и  параллельны
третьей прямой
параллельны
третьей прямой  , то они
параллельны между собой.
, то они
параллельны между собой.

Доказательство. В самом деле,
если бы прямые  и
и  пересекались в
некоторой точке
пересекались в
некоторой точке  , то получилось бы,
что через эту точку можно было бы провести две прямые
, то получилось бы,
что через эту точку можно было бы провести две прямые  и
и  , параллельные
прямой
, параллельные
прямой  , а это
противоречило бы аксиоме параллельности прямых.
, а это
противоречило бы аксиоме параллельности прямых.
Что и требовалось доказать.
Верно следующее утверждение: если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

Доказательство. Пусть  ,
,  . Докажем, что
. Докажем, что  .
.
Так как  , то
, то  . При пересечении
параллельных прямых
. При пересечении
параллельных прямых  и
и
 секущей
секущей
 образуются равные
соответственные углы. Значит,
образуются равные
соответственные углы. Значит,  . Следовательно,
. Следовательно,  .
.
Что и требовалось доказать.
А теперь давайте рассмотрим решения некоторых задач по теме «параллельные прямые».
Задача.
При пересечении двух параллельных
прямых секущей образовано  углов.
углов.  . Найдите остальные
углы.
. Найдите остальные
углы.

Так как прямые АВ и CD параллельны, то  , как внешние
накрест лежащие.
, как внешние
накрест лежащие.
 , как
соответственные.
, как
соответственные.
 , как вертикальные
углы.
, как вертикальные
углы.
 , как внутренние
накрест лежащие.
, как внутренние
накрест лежащие.
 по свойству смешных
углов.
по свойству смешных
углов.
 , как внешние
накрест лежащие.
, как внешние
накрест лежащие.
 , как
соответственные.
, как
соответственные.
 , как вертикальные.
, как вертикальные.
Задача.
Высота треугольника делит угол, из
вершины которого она опущена, на части, равные соответственно  и
и  . Определите все
углы этого треугольника.
. Определите все
углы этого треугольника.

Пусть высота выходит из вершины В
треугольника  . Т.е.
. Т.е.  . Тогда
. Тогда  ,
,  . А значит,
. А значит,  .
.
Рассмотрим треугольник  . Он прямоугольный,
так как
. Он прямоугольный,
так как  высота. Т.е. имеем,
высота. Т.е. имеем,
 ,
,  по условию.
Напомню, сумма острых углов прямоугольного треугольника равна 900. А
тогда несложно вычислить угол
по условию.
Напомню, сумма острых углов прямоугольного треугольника равна 900. А
тогда несложно вычислить угол  . Он равен
. Он равен  .
.
Рассмотрим треугольник  . Он прямоугольный,
так как
. Он прямоугольный,
так как  высота.
Т.е. имеем,
высота.
Т.е. имеем,  ,
,  градусов по
условию. Найдем угол
градусов по
условию. Найдем угол  . Он равен
. Он равен  .
.
Задача.
Докажите, что биссектриса одного из внутренних односторонних углов при параллельных прямых и секущей отсекает на одной из параллельных прямых отрезок, равный отрезку секущей.

Доказательство. Пусть  и
и  – биссектриса
– биссектриса  . Докажем, что
. Докажем, что  .
.
 , так как
, так как  – биссектриса
– биссектриса  .
.
 , как накрест
лежащие при параллельных прямых.
, как накрест
лежащие при параллельных прямых.
Из этих равенств следует, что  .
.
Значит, треугольник  – равнобедренный,
по признаку равнобедренного треугольника. Следовательно,
– равнобедренный,
по признаку равнобедренного треугольника. Следовательно,  .
.
Т.е. мы получили, что биссектриса одного из внутренних односторонних углов при параллельных прямых и секущей отсекает на одной из параллельных прямых отрезок, равный отрезку секущей.
Что и требовалось доказать.
Итоги урока
На этом уроке мы говорили о параллельных прямых. Вспомнили признаки параллельных прямых. А затем рассмотрели решения некоторых задач по теме «параллельные прямые».

 Получите свидетельство
Получите свидетельство Вход
Вход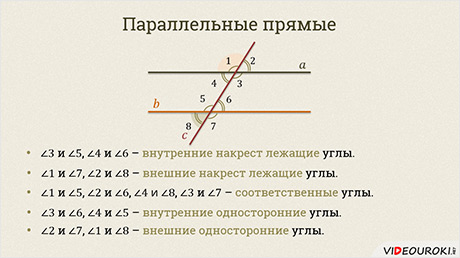



 0
0 5625
5625



