Графики зависимости кинематических величин от времени при РПД и РУД

Механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

В свою очередь механическое движение бывает двух видов — равномерным, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.

Вспомним основные формулы для равномерного и неравномерного движения.

Если движение равномерное, то:

Скорость тела не меняется с течением времени. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени

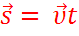
Это уравнение называется уравнением перемещения.

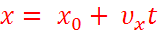
Это уравнение называется кинематическим уравнением равномерного движения.

Для равноускоренного движения:

Ускорение тела не изменяется с течением времени. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло.

Уравнение скорости для равноускоренного движения имеет вид:

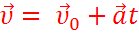
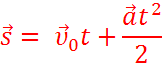
Это уравнение называется уравнением перемещения для равноускоренного движения.

Кинематическое уравнение равноускоренного движения имеет вид:

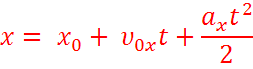
Для большей наглядности движение можно описывать с помощью графиков.

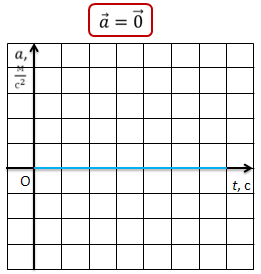
Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, то полученный график будет выражать зависимость ускорения тела от времени.

Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.

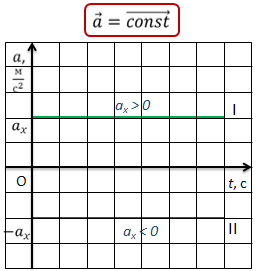
Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, или под осью времени, если тело движется замедленно.

Если же по оси ординат откладывать значение не ускорения, а скорости тела, то можно получить график скорости.

Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. График скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.

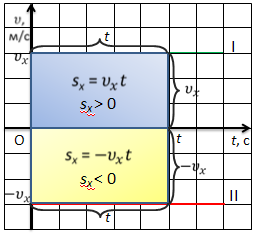
Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта зависимость состоит в том, что скорость с течением временине меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.

По графику скорости можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади закрашенного прямоугольника: верхнего, если тело движется в сторону положительного направления, или нижнего — в случае движения тела в отрицательном направлении.

Действительно, площадь прямоугольника равна произведению его сторон:

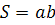
где a и b стороны прямоугольника.

Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, или отрицательным, если проекция вектора скорости отрицательна.

При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле

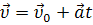
Т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненных к оси времени. Причем, чем больше угол наклона, тем большую скорость имеет тело. На представленном графике прямая 1 соответствует движению с положительным ускорением и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением и начальной скоростью равной нулю.

По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника для второго тела. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В представленном случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости. При этом проекция перемещения для первого тела будет положительной.

Для второго тела, прямоугольного треугольника, проекция перемещения равна половине произведения его катетов. Т.е. это время и конечная скорость тела. Проекция перемещения — отрицательна.

Теперь рассмотрим зависимость пройденного пути от времени.

Как и в предыдущих случаях, по оси абсцисс будем откладывать время, с момента начала движения, а по оси ординат — путь.

Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.

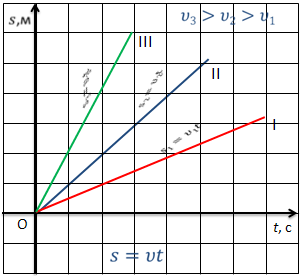
При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем большая скорость движения тела.

При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.

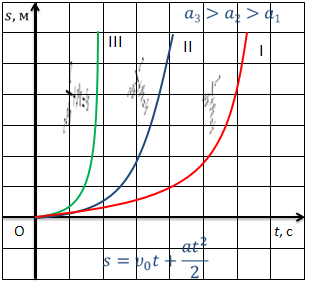
Теперь перейдем к рассмотрению зависимости перемещения от времени.

Рассмотрим равномерное движение. Т.к. при равномерном движении перемещение линейно зависит от времени, то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.

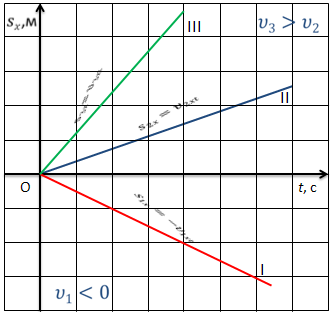
Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго. А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.

Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения тела.

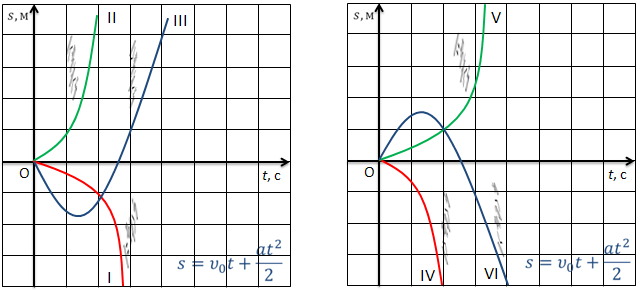
Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю. Для 2-го тела ускорение и начальная скорость тела больше нуля. Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля. У 4-го тела начальная скорость и ускорение меньше нуля. Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю. Шестое тело двигается замедленно с некоторой начальной скоростью.

Рассмотрим зависимость координаты тела от времени.

Если по оси абсцисс откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по оси ординат — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения). Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.

График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.

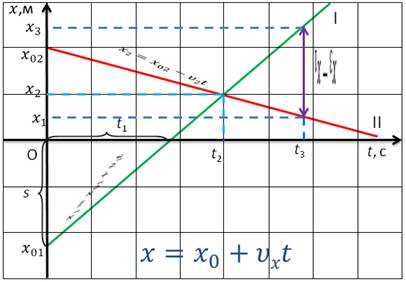
В случае прямолинейного движения тела графики дви­жения дают полное решение за­дачи механики, так как они позволяют найти поло­жение тела в любой момент времени, в том числе и в моменты времени, предшество­вавшие начальному моменту (если предполо­жить, что тело двигалось с такой же ско­ростью и до начала отсчета времени).

С помощью графика движения можно определить:

– координаты тела в любой момент времени;

– путь, пройденный телом за некоторый промежуток времени;

– время, за которое пройден какой-то путь;

– кратчайшее расстояние между телами в любой момент времени;

– момент и место встречи и т.д.

По виду графиков зависи­мости координаты от времени можно судить и о скорости дви­жения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изме­нение координаты за одно и то же время).

При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

Основные выводы:

– Механическое движение для большей наглядности можно описывать с помощью графиков:

– Зависимости скорости от времени

– Ускорения от времени

– Координаты тела от времени

– И зависимости перемещения тела от времени, в течении которого это перемещение произошло.