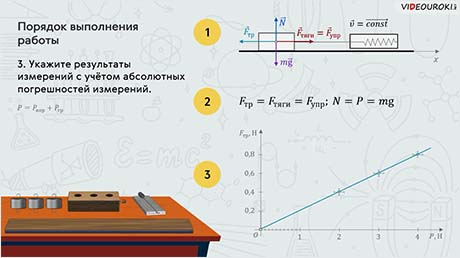
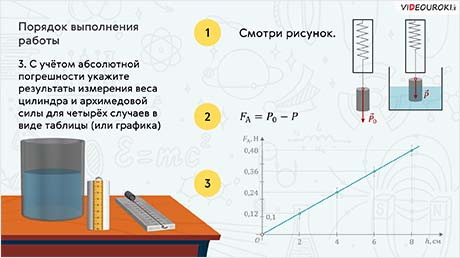
Прямолинейным равноускоренным движением называется движение, при котором скорость тела за любые равные промежутки времени изменялась на одинаковую величину. И основной характеристикой такого движения являлось ускорение — это физическая векторная величина, характеризующая быстроту изменения скорости.
Как определить координату тела, пройденный путь и перемещение при прямолинейном равноускоренном движении?
Это можно сделать, если рассмотреть прямолинейное равноускоренное движение как набор большого количества очень малых равномерных перемещений тела.
Первым решил задачу местоположения тела в определённый момент времени при ускоренном движении итальянский учёный Галилео Галилей. Галилей использовал наклонную плоскость с гладкой канавкой посередине, по которой скатывались латунные шары. По водным часам он засекал определённый интервал времени и фиксировал расстояния, которые за это время преодолевали шары. Галилей выяснил, что если время увеличить в два раза, то шары прокатятся в четыре раза дальше (т.е. зависимость квадратичная). Это опровергало мнение Аристотеля, что скорость шаров будет постоянной.
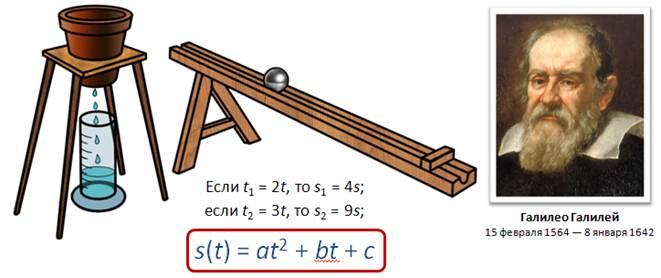
Получим формулу для определения перемещения при равноускоренном движении графическим методом.
Известно, что при равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле
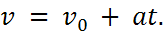
Т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой.
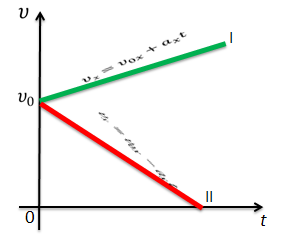
Прямая 1 соответствует движению с положительным ускорением (скорость увеличивается), прямая 2 — движению с отрицательным ускорением (скорость убывает).
График скорости разобьем на маленькие прямоугольные участки. Каждый участок будет соответствовать определённой постоянной скорости.
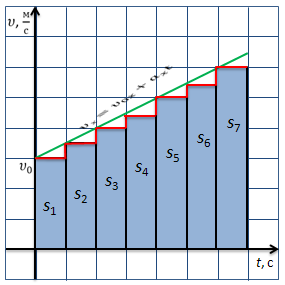
Необходимо определить пройденный путь за первый промежуток времени. Запишем формулу
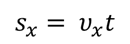
Теперь посчитаем суммарную площадь всех имеющихся у нас фигур. А сумма площадей при равномерном движении – это полный пройденный путь.
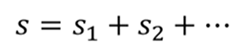
Обратите внимание, от точки к точке скорость будет изменяться, тем самым можно получить путь, пройденный телом именно при прямолинейном равноускоренном движении.
Заметим, что при прямолинейном равноускоренном движении тела, когда скорость и ускорение направлены в одну сторону, модуль перемещения равен пройденному пути, поэтому, когда определяется модуль перемещения, то определяется и пройденный путь.
В данном случае можно говорить, что модуль перемещения будет равен площади фигуры, ограниченной графиком скорости и осью времени.
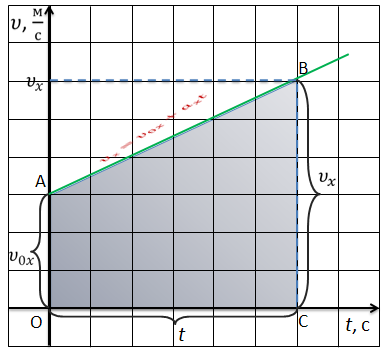
Фигура, ограниченная графиком скорости и осью времени есть не что иное, как прямоугольная трапеция. Из математики известна формула для нахождения площади трапеции. Площадь трапеции равна произведению половины суммы её оснований на высоту.
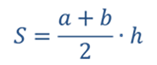
Следовательно, перемещение за все время tчисленно равно площади трапеции ОАВС. В нашем случае длина одного из оснований численно равна υoх, длина другого — υх. Высота же ее численно равна t. Отсюда следует, что перемещение равно:
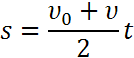
Подставим в эту формулу вместо υ равную ей величину υ0 + at.Тогда
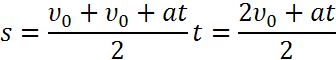
Разделив почленно числитель на знаменатель, получим
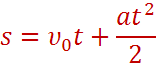
Это есть уравнение перемещения в проекциях на ось координат.
При пользовании этой формулой нужно помнить, что s, υ0 и а могут быть как положительными, так и отрицательными — ведь это проекции векторов пути, начальной скорости и ускорения на ось X.
Теперь вспомним, что пройденный путь, равный в нашем случае модулю перемещения, выражается разностью: s = x – x0
Если в уравнение подставить полученное нами выражение для S, то запишем закон, по которому движется тело при прямолинейном равноускоренном движении:
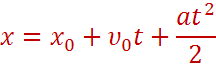
Это уравнение называется основным кинематическим уравнением равноускоренного движения.
Если тело движется из состояния покоя, график проходит через начало координат, фигура под графиком – прямоугольный треугольник, площадь которого равна половине произведения катетов.
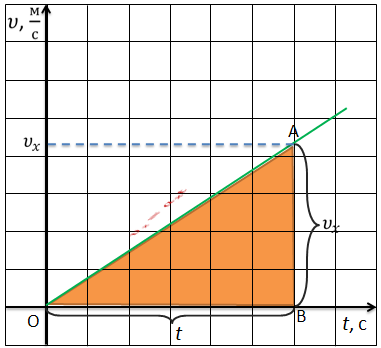
Тогда формула для определения перемещения принимает вид:
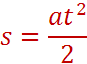
Это уравнение перемещения при равноускоренном движении без начальной скорости.
Тогда
x = x0 + at2/2
Это кинематическое уравнение равноускоренного движения , без начальной скорости.
Рассмотрим некоторые важные зависимости между величинами равноускоренного движения. Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени. Значит, пути, пройденные телом за 1 с, 2 с, 3 с, 4 с будут относиться как квадраты последовательных натуральных чисел.
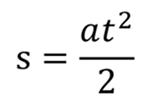

Для любого равноускоренного движения, пути, пройденные телом за любые равные промежутки времени, будут относиться как последовательный ряд нечетных чисел.
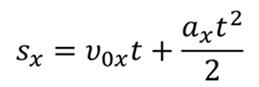

Основные выводы:
– Перемещение тела за все время t численно равно площади трапеции, ограниченной графиком скорости и осью времени.
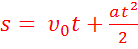 —
уравнениеперемещения
—
уравнениеперемещения
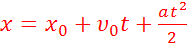 —
кинематическое
уравнение
равноускоренного движения
—
кинематическое
уравнение
равноускоренного движения
– Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени.
– Для любого равноускоренного движения, пути, пройденныетеломза любые равные промежутки времени, будутотноситьсякакпоследовательный ряд нечетных чисел.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 63144
63144