Вопросы занятия:
· вспомнить, что называется углом между векторами;
· повторить такое действие над векторами, как скалярное произведение;
· повторить, как находится скалярное произведение векторов, если даны координаты этих векторов.
Материал урока
И начнём мы наше повторение с понятия угла между векторами. Давайте вспомним как мы вводили это понятие.
Изобразим произвольные векторы:
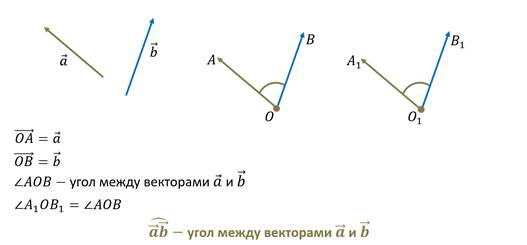
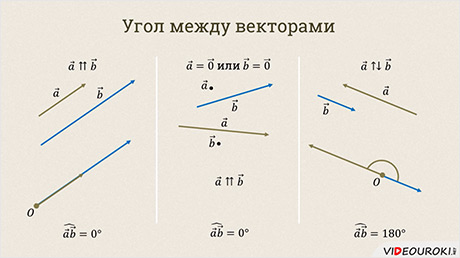
Теперь давайте рассмотрим, как определить угол между коллинеарными сонаправленными векторами. Если мы отложим эти векторы от одной точки, то они будут лежать на одной прямой. Поскольку они направлены в одну сторону, то нетрудно увидеть, что угол между сонаправленными векторами равен нулю.
Поскольку любой нулевой вектор сонаправлен с любым вектором, то, значит и угол между векторами, один из которых нулевой – равен нулю.
Теперь давайте рассмотрим случай, когда нам необходимо определить угол между противоположно направленными векторами. Отложим их от одной точки. Нетрудно увидеть, что в таком случае, угол между ними равен 180°.
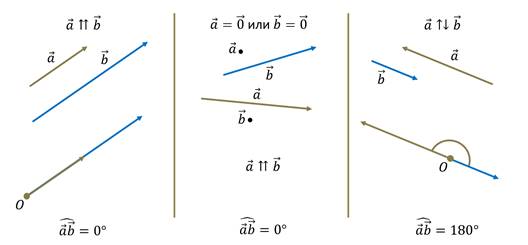
Если же угол между векторами равен 90°, то такие вектора называются перпендикулярными.
Когда мы повторяли тему угол между прямыми, то говорили, что углом между прямыми будет острый угол, который получается при пересечении этих прямых.
Для векторов это определение не совсем верно. Угол между векторами может быть как острым, так и тупым, но не больше 180°.
Рассмотрим несколько примеров.
Пример.

Прежде чем перейти к повторению скалярного произведения, давайте ещё раз вспомним действия, которые можно совершать над векторами. Вектора можно складывать (по правилу треугольника или параллелограмма), вектора можно вычитать. Вектор можно умножить на число.
Сегодня мы с вами повторим как же перемножать вектора.
Произведению векторов мы давали такое определение.
Определение.
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
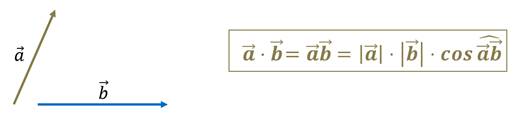
Теперь давайте вспомним важное замечание.
Замечание.
Результатом скалярного произведения векторов является число, в отличии от сложения, вычитания и умножения вектора на число. При этих операциях результатом всегда является вектор.
Отдельно рассматривается случай, когда скалярное произведение равно нулю. Мы знаем, что произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
Поскольку в произведении у нас присутствуют длины векторов, то скалярное произведение равно нулю тогда, когда хотя бы один из векторов – нулевой.
Если же оба вектора ненулевые, то должен быть равен нулю косинус угла между ними.
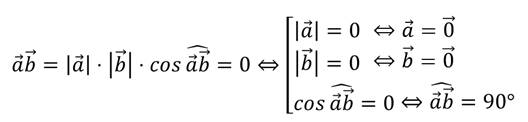
Вспоминая таблицу значений косинуса для некоторых углов из промежутка от 0° до 180°, нетрудно увидеть, что косинус равен нулю для угла в 90°. То есть скалярное произведение будет равно нулю в случае ненулевых векторов только тогда, когда эти векторы перпендикулярны.
Поскольку в произведении присутствуют длины векторов, то очевидно, что произведение первых двух множителей всегда больше нуля. Но косинус углов из промежутка от 0° до 180° может принимать как положительные, так и отрицательные значения, то есть скалярное произведение векторов может быть и положительным и отрицательным. Положительным оно будет тогда, когда угол между векторами не более 90°, а отрицательным – тогда, когда угол между векторами лежит в промежутке от 90° до 180°. Обратите внимание, что ни в один из промежутков мы не включили угол 90°. Потому что если угол между векторами равен 90°, то скалярное произведение таких векторов равно нулю.
Теперь давайте попробуем найти скалярное произведение сонаправленных векторов.
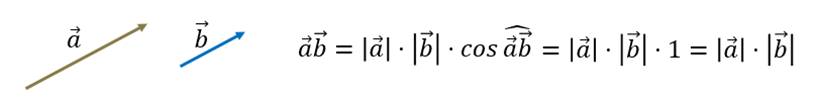
Теперь давайте попробуем найти скалярное произведение противоположно направленных векторов.
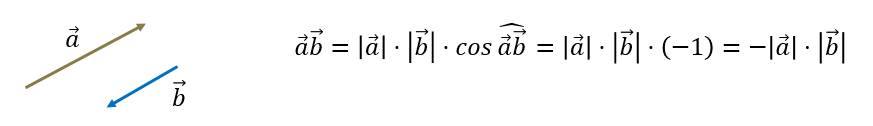
Теперь давайте вспомним как вычисляется скалярное произведение вектора на самого себя. Такое произведение называют скалярным квадратом. Очевидно, что каждый вектор сонаправлен сам себе, то есть скалярный квадрат вектора равен квадрату его длины.
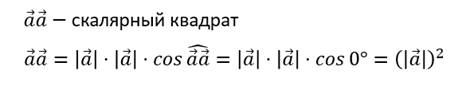
Рассмотрим пример.
Пример.

Поскольку каждый вектор имеет координаты в координатной плоскости, то давайте вспомним, как найти скалярное произведение векторов через их координаты.
Повторим теорему.
Теорема.

Доказательство.
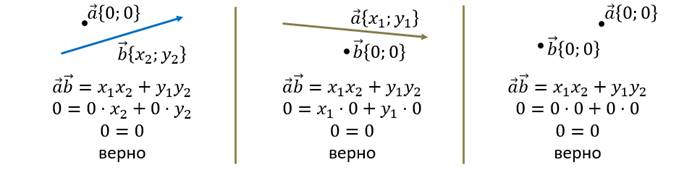
Теперь давайте рассмотрим пару ненулевых векторов.
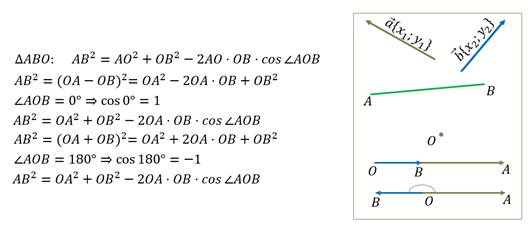
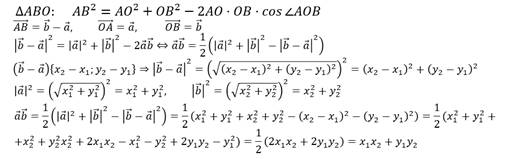
Читают эту формулу так. Скалярное произведение векторов равно сумме произведений их соответствующих координат.
Вспомним следствия из доказанной теоремы.
Следствие 1.

Следствие 2.

Рассмотрим пример.
Пример.

Итоги урока
Сегодня на уроке мы вспомнили, что называется углом между векторами. Вспомнили такое действие над векторами как скалярное произведение. Повторили как находится скалярное произведение векторов, если даны координаты этих векторов.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 7310
7310

