Теорема синуса, косинуса. Решение треугольников

Вопросы занятия:

·  вспомнить формулировки и доказательства теорем синуса и косинуса;

·  повторить, что значит «решить треугольник»

Материал урока

И начнём мы с вами с того, что вспомним формулировку теоремы синусов.

Она звучит так:

Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство.

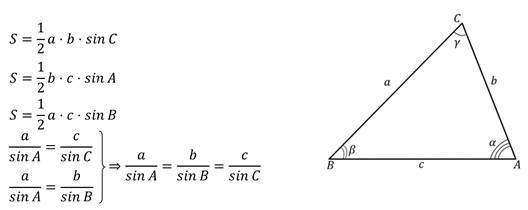
Расширенная теорема синусов.

Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.

Доказательство.

Что и требовалось доказать.

Теперь давайте вспомним теорему косинусов.

Теорема косинусов.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.

Доказательство.

Частным случаем теоремы косинусов является теорема Пифагора.

Давайте рассмотрим прямоугольный треугольник и запишем для него теорему косинусов.

Именно поэтому теорему косинусов называют обобщённой теоремой Пифагора.

Рассмотрим несколько примеров.

Пример.

Рассмотрим ещё один пример.

Пример.

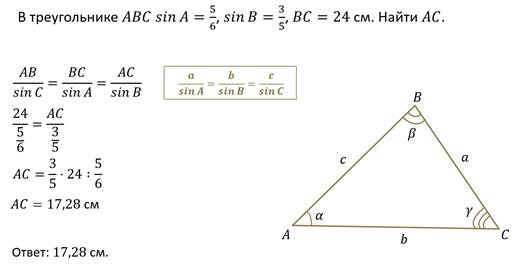
Рассмотрим ещё один пример.

Пример.

Теперь давайте вспомним, что значит решить треугольник.

Определение.

Решить треугольник – это значит найти все его элементы (три стороны и три угла) по каким-нибудь известным трём элементам, определяющим треугольник. К задачам такого плана относятся следующие задачи: решение треугольника по трём сторонам; решение треугольника по трём углам; решение треугольника по двум сторонам и углу между ними; решение треугольника по двум сторонам и углу, не лежащего между ними; решение треугольника по стороне и прилежащим к ней углам; решение треугольников по стороне и произвольным двум углам.

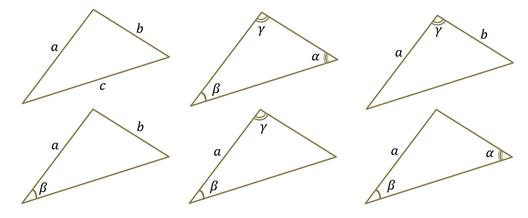
Рассмотрим каждый вид таких задач отдельно.

Начнём с решения треугольника по трём углам.

Запишем теорему синусов и косинусов и подумаем, с помощью какой из них можно решить треугольник.

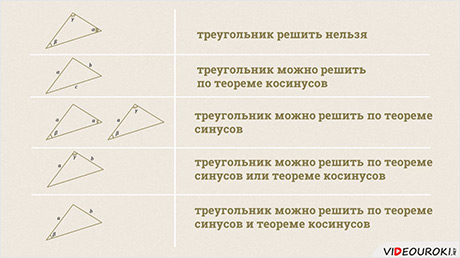
Обе эти теоремы содержат длины сторон, поэтому зная только углы треугольника нельзя найти длины сторон треугольника. То есть зная только три угла, решить треугольник нельзя.

Попробуем теперь решить треугольник по трём сторонам.

Зная длины всех сторон треугольника, по теореме косинусов можно найти косинусы всех углов треугольника.

А, зная косинус угла, сам угол найти несложно.

Для этого можно воспользоваться либо калькулятором либо таблицами Брадиса.

Значит в этом случае решить треугольник можно с помощью теоремы косинусов.

Следующим мы рассмотрим решение треугольника по стороне и прилежащим к ней углам.

Сразу замечаем, что третий угол найти нетрудно, он равен разности 180 градусов и известных углов.

Запишем теорему синусов.

Из каждого равенства, мы можем найти сторону треугольника. Таким образом, зная длину одной стороны и величину двух прилежащих к ней углов, можно найти все остальные элементы треугольника, используя теорему синусов.

Нетрудно увидеть, что условие: углы прилежащие к стороне здесь не существенно. Поскольку даже если нам известны два любых угла треугольника, то мы всегда можем найти третий угол этого треугольника. Тогда можно сказать, что, зная одну сторону и два любых угла можно решить треугольник с помощью теоремы синусов.

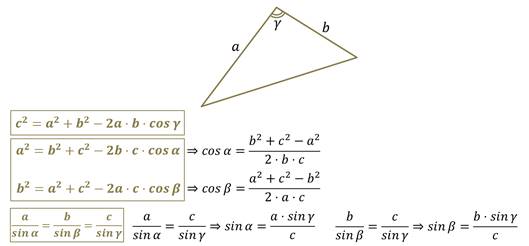
Теперь давайте рассмотрим способ решения треугольника по двум сторонам и углу между ними.

Третью сторону можно найти с помощью теоремы косинусов.

А углы отыскать или с помощью теоремы косинусов, как мы это делали, когда решали треугольник по трём сторонам. Или с помощью теоремы синусов. То есть в таком случае можно решить треугольник используя или теорему синусов или теорему косинусов.

Теперь давайте посмотрим, а можно ли решить треугольник, если мы знаем две стороны и угол, который не лежит между ними. Да, можно. Для этого по теореме синусов надо найти второй угол треугольника, а затем и третий угол и по теореме косинусов найти третью сторону треугольника. То есть и в этом случае треугольник можно решить с помощью теоремы синусов и теоремы косинусов.

Итак, давайте обобщим.

Решим задачу.

Пример.

Итоги урока

Сегодня на уроке мы с вами вспомнили формулировки и доказательства теорем синуса и косинуса. Повторили, что значит решить треугольник.