Понятие синуса, косинуса, тангенса и котангенса

Вопросы занятия:

·  вспомнить, зачем и как появились понятия синуса, косинуса, тангенса и котангенса;

·  повторить, как находятся координаты произвольной точки;

·  вспомнить таблицу значений синуса, косинуса, тангенса, котангенса для некоторых углов из промежутка от 0° до 180°;

·  повторить основное тригонометрическое тождество и формулы приведения.

Материал урока

Прежде всего, давайте вспомним, зачем и как появились понятия синус, конус, тангенс и котангенс.

Появились эти понятия тогда, когда стало необходимым вычислить высоту дерева, не залезая на него.

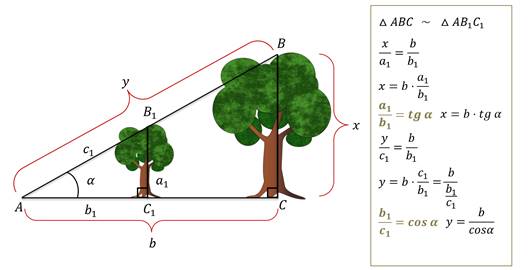
Таким образом, нам удалось, не влезая на дерево, определить его высоту и расстояние от наблюдателя до вершины дерева. Так и были введены понятия тангенс и косинус.

С понятиями синус, косинус, тангенс, котангенс мы знакомились в прямоугольном треугольнике. Давайте вспомним основные правила, связанные с этими величинами.

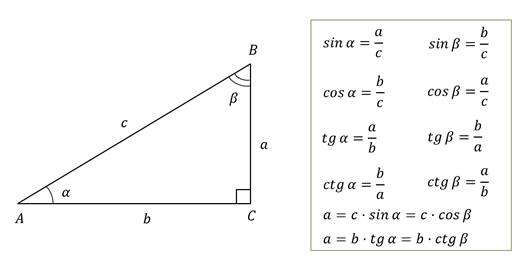
Давайте решим задачу.

Пример.

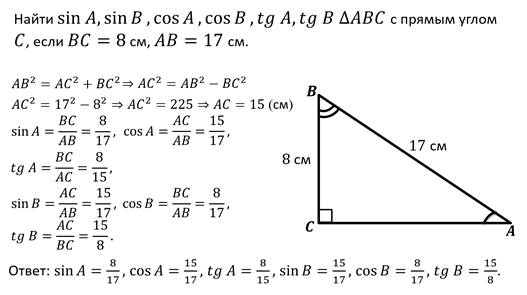
Но помимо прямоугольного треугольника, мы рассматривали понятия: синус, косинус, тангенс, котангенс для произвольного угла из промежутка от 0° до 180°.

Давайте вспомним, как мы это делали.

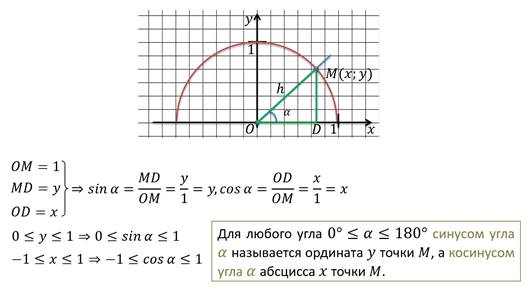
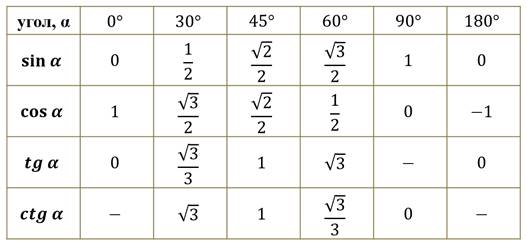
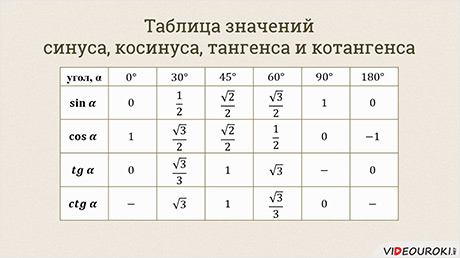
Мы с вами составляли таблицу значений для синуса, косинуса некоторых углов из промежутка от 0° до 180°. Повторим её.

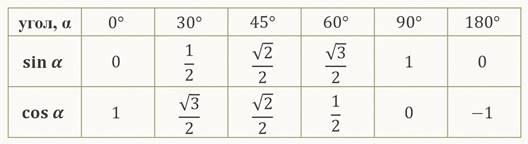
Пример.

Решим теперь обратную задачу.

Задача.

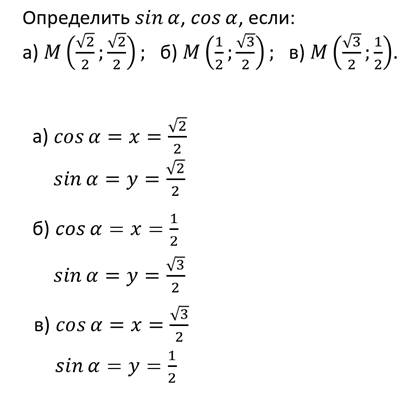
Теперь давайте вспомним, как можно определить координату любой точки координатной плоскости выразить через синус, косинус угла.

Рассмотрим задачу.

Задача.

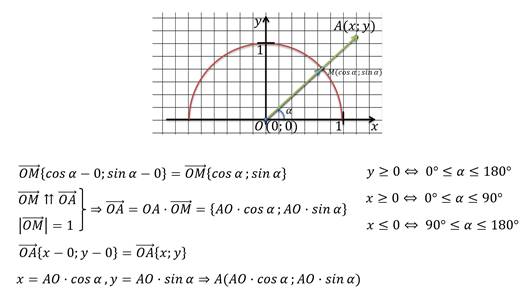
Рассмотрим пример.

Пример.

Тангенсом острого угла мы называли отношение синуса угла альфа на косинус угла альфа. Эта же формула справедлива для произвольного угла от 0° до 180°.

Решим задачу.

Задача.

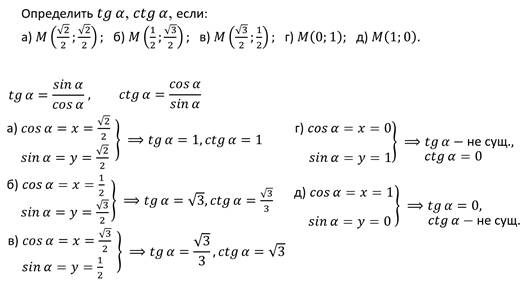
Давайте занесём полученные данные в таблицу и составим таблицу синусов, косинусов, тангенсов и котангенсов для углов 0°, 30°, 45°, 60°, 90°, 180°.

Изучая тригонометрию, мы с вами вывели и доказали несколько основных формул. Так, мы с вами доказали основное тригонометрическое тождество. Записывается оно так:

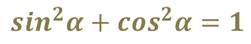
Еще мы с вами выводили формулы приведения:

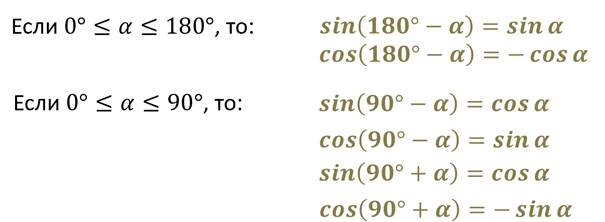
Решим несколько задач.

Пример.

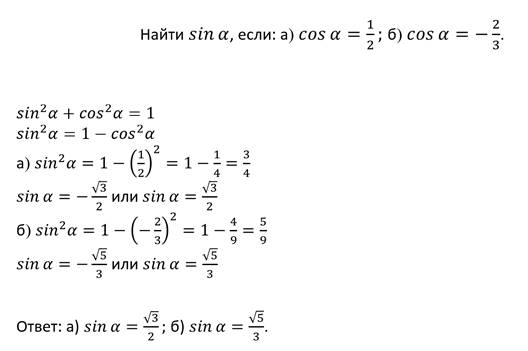
Решим задачу.

Задача.

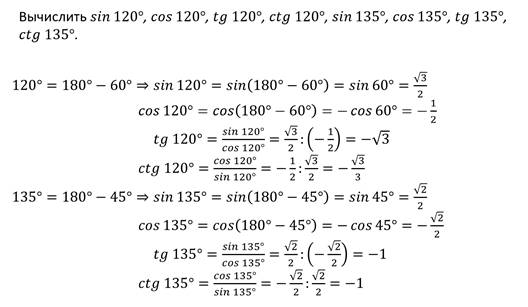
Итоги урока

Сегодня на уроке мы вспомнили такие понятия как синус, косинус, тангенс, котангенс. Повторили, как найти координаты произвольной точки пространства, вспомнили таблицу значений синуса, косинуса, тангенса, котангенса для некоторых углов из промежутка от нуля до ста восьмидесяти градусов. Повторили основное тригонометрическое тождество и формулы приведения.