Электрическая проводимость различных веществ. Электронная проводимость металлов

Как мы уже свами знаем, проводниками электрического тока могут быть вещества и в твёрдом, и в жидком, и в газообразном состояниях. Возникает закономерный вопрос: а какие частицы являются носителями электрического заряда в той или иной среде?

Мы уже с вами говорили о том, что в металлах носителями заряда являются свободные электроны. Наряду с металлами хорошими проводниками являются водные растворы или расплавы электролитов. Заряженные частицы, обеспечивающие существование электрического тока в электролитах, образуются в результате электролитической диссоциации, то есть распада молекул растворяемого вещества на ионы под действием молекул растворителя. Иными словами, в электролитах носителями заряда являются положительные и отрицательные ионы.

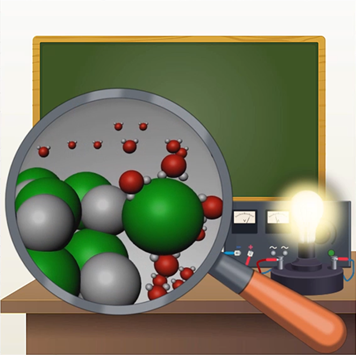
При определённых условиях газ также может являться хорошим проводником электрического тока. Носителями тока в этом случае выступают ионы и электроны.

А как вы думаете, возможен ли ток в вакууме? Для начала, давайте вспомним, что вакуум — это такое состояние газа в сосуде, при котором длина свободного пробега заряженных частиц превышает размеры сосуда. Проще говоря, вакуум — это идеальный изолятор, так как в нём отсутствуют свободные носители заряда.

Однако, если в сосуд с вакуумом поместить два электрода, один из которых — это подогреваемый спиралью катод, а второй — холодный анод, включённый в электрическую цепь, то электроны, вырвавшиеся с поверхности катоды, придут в упорядоченное движение и цепь замкнётся. Следовательно, носителями тока в вакууме являются электроны.

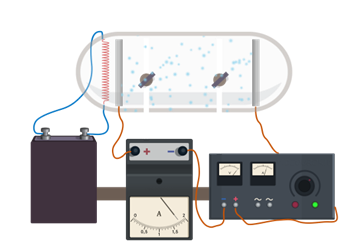
Также мы с вами говорили о том, что в природе существуют вещества, занимающие промежуточное положение между проводниками и диэлектриками — это полупроводники. В них носителями тока являются свободные электроны и дырки.

На сегодняшнем уроке мы с вами остановимся на подробном рассмотрении электронной проводимости металлов. Впервые она была экспериментально подтверждена немецким физиком-экспериментатором Эдуардом Рикке в 1901 году. Суть его опыта достаточно проста. Он взял проводник, состоящий из трёх отполированных и плотно прижатых друг к другу двух медных и одного алюминиевого цилиндров известной массы, и в течение года пропускал по ним ток одного и того же направления. За это время через проводник прошёл чудовищный заряд — более чем 3,5 МКл. После завершения опыта, Рикке опят взвесил цилиндры. Оказалось, что их массы остались неизменными. Более того, в местах контакта цилиндров также никаких изменений не произошло. Этот, на первый взгляд, простой эксперимент послужил доказательством того, что перенос заряда при прохождении тока в металлах не сопровождается химическими процессами и переносом вещества, а осуществляется частицами, которые являются общими для всех металлов, — электронами.

Убедительное доказательство электронной природы тока в металлах было получено в 1913 году в опытах русских физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американским физиком Ричардом Толменом и шотландским физиком Томасом Стюартом в 1916 году.

Идея обоих опытов такова.  Берётся катушка с большим числом витков из тонкой проволоки, концы которой припаяны к двум металлическим дискам, изолированным друг от друга. С помощью скользящих контактов катушка подключается к гальванометру. Затем её приводят в быстрое вращение (до полутора тысяч оборотов в минуту), и — резко останавливают. При таком торможении катушки в цепи возникает кратковременный ток, обусловленный инерцией носителей заряда

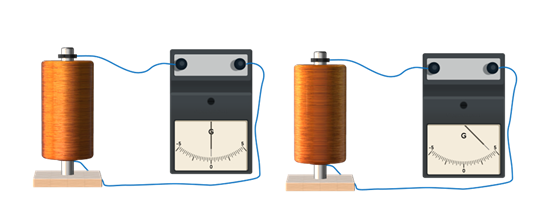
По направлению отклонения стрелки гальванометра было установлено, что электрический ток создают отрицательно заряженные частицы. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе:

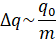
Поэтому, измеряя заряд, проходящий через гальванометр за всё время существования тока в цепи, удалось определить отношение q₀/m (то есть удельный заряд). Он оказался равным одной целой и восьми десятым на десять в одиннадцатой степени кулон на килограмм, что оказалось очень близко к величине удельного заряда электрона, найденному ранее из других опытов.:

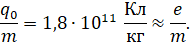
Так было экспериментально доказано, что носителями свободных зарядов в металлах являются электроны.

В 1900—1904 гг., немецкий физик Пауль Друде и голландский физик Хендрик Лоренц разработали классическую электронную теорию проводимости металлов. Согласно этой теории любой металлический проводник можно рассматривать как физическую систему, состоящую из двух подсистем: свободных электронов с концентрацией ~10²⁸ м^–3 и положительно заряженных ионов, колеблющихся около положений равновесия.

Появление свободных электронов в металлическом кристалле упрощённо объяснить можно так. Электроны, находящиеся на внешних оболочках атомов, слабо связаны со своими ядрами. А при образовании кристалла электроны начинают взаимодействовать не только со своими ядрами, но и с ядрами соседних атомов. В результате внешние электроны отрываются и могут двигаться по всему кристаллу в любом направлении, подобно частицам идеального газа. Эти электроны и называются свободными или электронами проводимости.

А совокупность свободных электронов в кристаллической решётке металла называют электронным газом.

Если к проводнику приложено внешнее электрическое поле, то на тепловое движение свободных электронов накладывается ещё направленное движение под действием сил электрического поля, что и порождает электрический ток.

При этом считается, что движение электронов под действием сил электрического поля подчиняется законам классической механики, а их столкновения с ионами кристаллической решётки металла являются неупругими.

Модель электронного газа даёт возможность теоретически объяснить природу сопротивления и вывести закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов.

Итак, пусть электрон движется с ускорением 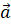 в направлении, противоположном направлению напряжённости электрического поля. Так как движение электрона подчиняется законам классической механики, то его ускорение мы можем определить на основании второго закона Ньютона:

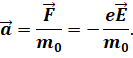
В записанной формуле m₀ — это масса электрона, а F — это постоянная сила, действующая на электрон со стороны электрического поля. Она равна произведению заряда электрона на напряжённость электрического в проводнике.

Тогда модуль средней скорости направленного движения электрона (она называется дрейфовой скоростью) линейно возрастает со временем:

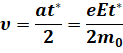
Здесь t* — это усреднённое время между двумя последовательными столкновениями электрона с ионами кристаллической решётки.

Дрейфовая скорость электрона не увеличивается в дальнейшем со временем, так как при столкновении с ионами кристаллической решётки электрон передаёт им кинетическую энергию, приобретённую в электрическом поле. Потом он опять ускоряется и процесс повторяется. В результате дрейфовая скорость электрона оказывается пропорциональной напряжённости электрического поля в проводнике.

Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряжённости этого поля равен отношению напряжения между его концами к длине проводника:

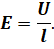
Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника: υ ~ U.

Теперь давайте с вами вспомним, что сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:

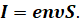
Но, как мы показали с вами выше, дрейфовая скорость пропорциональна разности потенциалов на концах проводника. Следовательно, сила тока пропорциональна разности потенциалов на концах проводника: I ~ U. В этом состоит качественное объяснение закона Ома на основе классической электронной теории проводимости металлов.

Для закрепления материала решим с вами небольшую задачу. Как изменится дрейфовая скорость электронов в проводнике, если при неизменной площади поперечного сечения и разности потенциалов на его концах, увеличить длину этого проводника в три раза?

В заключении урока отметим, что построить удовлетворительную количественную теорию движения электронов в металле на основе законов классической механики невозможно. А дело всё в том, что условия движения электронов в металле таковы, что для его описания классическая механика Ньютона неприменима. Этот факт подтверждается, например, зависимостью сопротивлений металлов от температуры. Так в классической теории металлов, в которой движение электронов рассматривается на основе второго закона Ньютона, сопротивление проводника пропорционально квадратному корню из температуры.

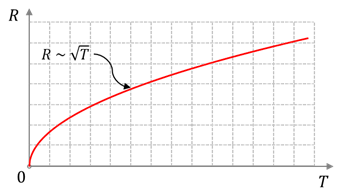
А вот эксперименты говорят, что эта зависимость линейная. Однако об этом мы с вами поговорим в следующий раз.