Последовательное и параллельное соединения проводников

От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию: электрической лампе, радиоприёмнику и так далее.

Совокупность устройств и элементов, предназначенных для протекания электрического тока, называют электрической цепью.

Любая электрическая цепь содержит, во-первых, источник тока, создающий необходимое напряжение, а во-вторых, нагрузку, то есть то устройство, в котором нужно создать ток и использовать одно из его действий. Нагрузкой может быть нагреватель или лампа накаливания (здесь используют тепловое действие тока), электродвигатель или звонок (используется магнитное действие тока), аккумулятор (это проявление химического действия тока). Звеньями же цепи являются соединительные провода и ключ, служащий для удобства и безопасности работы.

Рисунки, на которых изображены способы соединения электрических приборов в цепь, называются электрическими схемами.

Приборы на схемах принято обозначать условными знаками, часть из которых представлена на экране в виде таблицы.

Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного проводника, а из системы различных проводников, которые могут быть соединены между собой по-разному.

Рассмотрим простую цепь, составленную из источника ток, ключа и двух проводников. Обратите внимание на то, что в представленной цепи конец одного проводника соединяется с началом другого, его конец — с началом третьего и так далее. Проще говоря, проводники имеют по одной общей точке. Такое соединение проводников принято называть последовательным соединением.

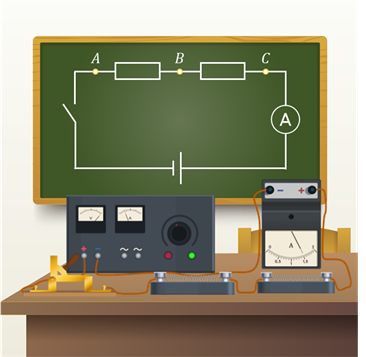
Как вы уже знаете, в проводниках, по которым течёт постоянный ток, электрический заряд не накапливается, и через любое поперечное сечение проводника за определённое время протекает один и тот же заряд. Следовательно, ток во всех частях последовательно соединённой цепи в каждый данный момент времени одинаков:

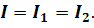
Напряжение же на концах каждого из проводников будет различно. Покажем это. Пусть I — это сила тока в цепи, R₁ и R₂ — сопротивления проводников, a U₁ и U₂ — напряжения на концах этих проводников.

На основании закона Ома мы с вами можем записать, что напряжения на концах проводников пропорциональны силе тока в цепи и их сопротивлениям:

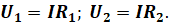
Разделив первое равенство на второе, получим, что при последовательном соединении напряжения на проводниках пропорциональны их сопротивлениям:

Только при таком распределении напряжений и становится возможным один и тот же ток во всех участках цепи.

А полное напряжение на обоих проводниках (или напряжение на полюсах источника тока) равно сумме напряжений на отдельных проводниках:

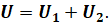
Это легко проверить, если измерить напряжение на концах обоих проводников и на двух проводниках одновременно.

Также записанное нами равенство вытекает из того, что напряжение есть величина, измеряемая работой, совершаемой при перемещении единицы заряда на данном участке цепи:

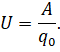
Работа же по перемещению заряда во всех последовательно соединённых проводниках равна сумме работ на отдельных проводниках.

Применяя закон Ома для всего участка цепи с последовательным соединением и для каждого проводника в отдельности, нетрудно показать, что полное сопротивление участка цепи равно сумме сопротивлений отдельных проводников:

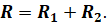
Совершенно аналогично можно показать, что в случае п последовательно соединённых проводников общее сопротивление участка цепи, состоящей из нескольких последовательно соединённых проводников, равно сумме сопротивлений отдельных проводников:

Рост сопротивления цепи при добавлении в неё новых проводников объясняется увеличением длины проводящей части. Поэтому сопротивление цепи становится больше сопротивления одного проводника.

На практике последовательное соединение нескольких проводников используется очень редко, например, в ёлочной гирлянде. Дело в том, что недостатком такого соединения является то, что в такую цепь можно подключать только тех потребителей, которые рассчитаны на одинаковую силу тока. Кроме того, если в такой цепи выключить ток в одном звене (например, перегорит одна из лампочек в гирлянде), то разрывается вся цепь.

Этих недостатков лишена цепь, в которой потребители соединены параллельно.

Параллельное соединение — это такое соединение проводников, при котором одни их концы соединены в один узел, другие концы — в другой узел.

Узлом принято называть точку разветвлённой цепи, в которой сходятся более двух проводников.

Следствием этого является то, что напряжение на каждом параллельно соединённом проводнике одинаково и равно напряжению на всём участке параллельно соединённых проводников:

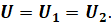
При параллельном соединении ток распределяется по проводникам так же, как поток воды, разветвляющийся на два параллельных канала. Количество воды, протекающее ежесекундно через неразвтвлённую часть потока воды, равно сумме количеств воды, протекающих ежесекундно через каждый из каналов.

Аналогично обстоит дело и с прохождением электрических зарядов через параллельно соединённые проводники. Включив амперметры в цепь до разветвления и в каждую ветвь разветвления, можно убедиться, что ток в неразветвлённой части цепи равен сумме токов, текущих в отдельных параллельно соединённых проводниках:

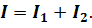
Этот опыт служит лишь подтверждением того, что в случае установившегося тока электрические заряды не скопляются в точках разветвления, а сколько их подходит к точкам разветвления, столько же и уходит.

Обозначим сопротивление каждого из разветвлённых участков цепи через R₁ и R₂, a напряжение во всей цепи через U. Теперь применим к каждой ветви закона Ома для участка цепи:

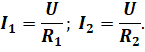
И выразим из этих формул напряжение.

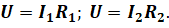
Так как напряжение на каждом параллельно соединённом проводнике одинаково, то давайте приравняем правые части последних двух равенств:

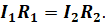
Отсюда находим, что токи в отдельных ветвях разветвлённой части цепи обратно пропорциональны их сопротивлениям:

Третья закономерность параллельного соединения определяет общее сопротивление разветвлённого участка. Учтём, что сила тока в цепи равна сумме сил токов в ветвях, а напряжение везде одинаково. Тогда, на основании закона Ома, получим, что величина, обратная сопротивлению участка параллельно соединённых проводников, равна сумме величин, обратных сопротивлению отдельных проводников:

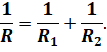
При этом общее сопротивление разветвлённой части цепи меньше наименьшего из сопротивлений её ветвей.

Нетрудно показать, что если в разветвление будет включено не два, а несколько проводников, то данная закономерность также будет выполняться:

Из этого равенства следует, что общее сопротивление участка цепи, состоящего из п параллельно соединённых проводников с одинаковым сопротивлением, в п раз меньше сопротивления одного из них:

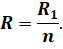
Параллельное соединение — это основной способ включения в электрическую цепь различных потребителей, так как в одну и ту же электрическую цепь могут быть включены самые различные потребители. Однако следует иметь в виду, что параллельно включаемые в данную цепь потребители должны быть рассчитаны на одно и то же напряжение, соответствующее напряжению в цепи.

Большинство задач на расчёт цепи сводится к определению токов, текущих в отдельных её участках, по заданному напряжению и по сопротивлениям отдельных проводников.

Для примера рассмотрим цепь, представленную на рисунке.

Пусть нам известно общее напряжение, питающее цепь, и сопротивления включённых в цепь резисторов (сопротивлением амперметра мы пренебрегаем, так как оно очень мало). Пусть нам надо найти силу тока, протекающего по каждому из резисторов.

Прежде всего мы должны установить, из скольких последовательных участков состоит наша цепь. Легко видеть, что таких участков три, причём второй и третий участки представляют собой разветвления. Обозначим сопротивления трёх последовательных участков нашей цепи через R_I, R_II, R_III.

Тогда всё сопротивление цепи выразится как сумма сопротивлений этих участков:

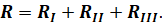
Общее сопротивление цепи необходимо знать, так как заданное общее напряжение можно отнести только к полному общему сопротивлению цепи. Применяя закон Ома, мы найдём полный ток, текущий в нашей цепи:

Нетрудно увидеть, что сила тока на первом резисторе равна силе тока во всей цепи:

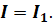
Для того чтобы найти токи в отдельных ветвях, надо предварительно найти напряжение на отдельных участках последовательных цепей. А поможет нам это сделать закон Ома:

Незабываем о том, что R_II и R_III — это эквивалентные сопротивления разветвлённых участков. Эти сопротивления мы с вами можем легко найти по закону параллельного соединения

Ну а дальше, зная напряжения на отдельных разветвлениях, найдём и токи в отдельных ветвях используя всё тот же закон Ома (при этом не забываем, что напряжение на концах всех параллельно соединённых проводников одно и то же):

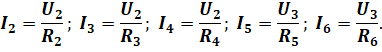
Таким образом, задача, поставленная перед нами, полностью решена.