На прошлом уроке мы с вами говорили об электрическом токе и его действиях. Очевидно, что различные действия тока зависят от силы протекающего тока. Напомним, что силой тока мы с вами назвали физическую величину, численно равную заряду, прошедшему через поперечное сечение проводника за единицу времени.
Таким образом, регулировать действия тока можно изменяя силу тока. Но для того чтобы получить возможность управлять током в цепи, нужно знать, от чего и как он зависит. Для установления этой зависимости возьмём резистор, который подключим в цепь с источником тока, выходное напряжение между клеммами которого можно регулировать. С помощью последовательно включённого амперметра и параллельно резистору вольтметра будем измерять силу тока и напряжение на спирали резистора.
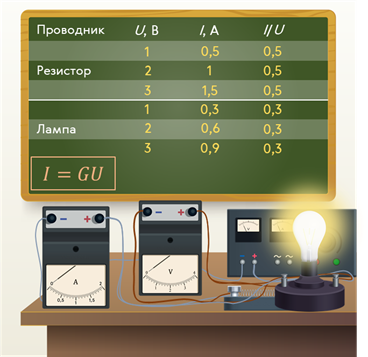
Меняя выходное напряжение в целое число раз, мы заметим, что изменяется и ток в цепи, и напряжение на концах проводника. При этом во сколько раз увеличивается напряжение на концах данного проводника, во столько же раз увеличивается и ток в нём.
Если взять другой проводник и повторить с ним те же самые опыты, то мы увидим, что ток и в этом проводнике строго пропорционален напряжению на концах проводника.
Обозначая напряжение на концах проводника через U, а ток — через I, можно записать, что сила тока в проводнике прямо пропорциональна приложенному напряжению:
I = GU.
В этой формуле величина G зависит от свойств проводника: чем больше G тем больше и ток в проводнике при одном и том же напряжении. Но для данного проводника при всех значениях тока и напряжения величина этого коэффициента остаётся постоянной и равной отношению силы тока к напряжению (при условии, что температура проводника не меняется):
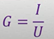
Следовательно, данная величина характеризует свойство данного проводника. Её назвали электропроводностью или просто проводимостью проводника. Единица электропроводности в Си названа сименсом (См), в честь немецкого учёного и предпринимателя Вернера фон Сименса.
Величина, обратная проводимости, называется сопротивлением проводника.
Давайте вспомним, что электрическое сопротивление — это скалярная физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока в нём.
Выражая в предыдущей формуле проводимость через сопротивление, получаем, что сила тока в данном участке цепи, прямо пропорциональна напряжению на этом участке и обратно пропорциональна его сопротивлению.
Этот закон впервые был открыт в тысяча восемьсот двадцать шестом (1826) году немецким учёным Генри Омом и называется законом Ома для участка цепи.
Как и всякую закономерность, закон Ома можно представить графически в виде так называемой вольт-амперной характеристики проводника, то есть зависимости силы тока в проводнике от напряжения на его концах.
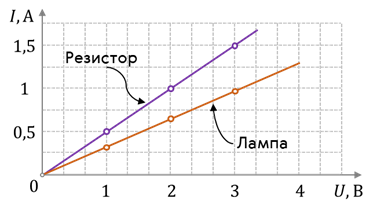
Как видим, график подтверждает прямую пропорциональную зависимость силы тока в проводнике от приложенного к нему напряжения.
Зная величину напряжения на концах проводника и ток в нём, по закону Ома можно вычислить сопротивление проводника, как отношение напряжения на концах проводника к силе тока в проводнике:
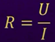
Из этой формулы можно вывести единицу сопротивления. Итак, за единицу сопротивления принимают сопротивление такого проводника, по которому проходит ток 1 А при напряжении на концах проводника 1 В. Эта единица сопротивления называется омом.
Для измерения сопротивления проводников необходимо было прежде всего выбрать образец, или, как принято называть, эталон сопротивления. В 1860 году Вернер Сименс предложил в качестве эталона ома принять сопротивление столбика ртути длиной 106,3 см, имеющего по всей длине постоянное сечение, равное 1 мм2, при температуре таяния льда.
В 1908 году Международный съезд электриков в Лондоне одобрил этот эталон и назвал его международным омом.
Стандарт ртутного столба применялся вплоть до 1948 года. В этом году на Генеральной конференции по мерам и весам ом был переопределён в абсолютном выражении, а не как стандарт эталона.
Следует отметить, что один ом — это достаточно маленькое сопротивление. Даже у спиралей обычных электроламп оно составляет сотни ом. Поэтому часто сопротивление выражают в килоомах (1 кОм = 103 Ом) и мегаомах (1 МОм = 106 Ом).
Набор образцовых сопротивлений, с которыми можно сравнивать измеряемые сопротивления, называется магазином сопротивлений. На рисунке вы видите устройство такого прибора.
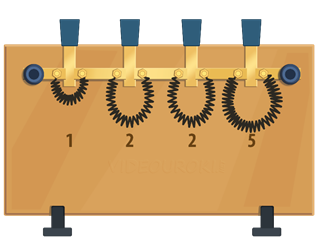
В его верхней части имеется группа металлических пластин, которые можно соединять друг с другом вставляемыми между ними штырями. К пластинам подключены металлические спирали с определёнными сопротивлениями. Если прибор включён в цепь крайними клеммами и штыри между пластинами вынуты, то ток идёт последовательно через все спиральки. Вынимая тот или иной штырь или группу штырей, мы можем при помощи магазина получить различные сопротивления в зависимости от величины сопротивления спиралей, имеющихся в магазине.
Исходя из определения сопротивления кажется, что оно зависит от силы тока и напряжения. Однако это не так. Чтобы понять от чего зависит сопротивление проведём несколько простых опытов с панелью сопротивлений.

Итак, включим в цепь источника тока половинку верхнего провода и измерим амперметром ток в цепи. Теперь подключим весь провод. Мы замечаем, что ток в цепи становится слабее. Причём слабее почти в два раза. Если взять более толстую проволоку (в нашем случае — это два верхних провода, сложенных вместе), то, как видим, ток в цепи становится в два раза сильнее. Наконец подключим самую нижнюю проволоку, изготовленную из железа, размеры которой такие же, что и у самой верхней проволоки. Легко заметить, что при одном и том же напряжении по железной проволоке идёт значительно меньший ток. Следовательно, проводники одинаковых размеров, но изготовленные из различных материалов, обладают неодинаковым сопротивлением.
Обобщив результаты наших опытов, мы можем утверждать, что: сопротивление проводника прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от вещества, из которого этот проводник изготовлен.
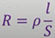
Сопротивление проводника зависит также от его температуры (но об этом в следующий раз).
Величина, обозначенная греческой буквой ρ, характеризует электрические свойства проводника. Она называется удельным сопротивлением проводника. Её численное значение зависит от единиц, в которых измерена длина и сечение проводника. В системе СИ единицей удельного сопротивления служит ом-метр, (Ом ∙ м).
Таким образом, удельное сопротивление проводника — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника, изготовленного из данного вещества и имеющего длину 1 м и площадь поперечного сечения 1 м2 (или сопротивлению куба с ребром 1 м).

В приводимой таблице указаны удельные сопротивления проводников для некоторых веществ при температуре 20 °С.
Наименьшим удельным сопротивлением, как видно из таблицы, обладают химически чистые серебро и медь. Металлические сплавы имеют значительно большее удельное сопротивление, чем чистые металлы, из которых состоят эти сплавы. А удельные сопротивления диэлектриков просто огромны.
В настоящее время большое применение в технике находят твёрдые вещества, механизм электрической проводимости у которых иной, чем у металлов, электролитов и газов. Такие вещества называются полупроводниками (но о них мы с вами будем говорить в ближайшее время). А сейчас, для закрепления материала, решим с вами такую задачу. Предположим, что у нас есть два цилиндрических проводника из одного и того же металла, которые имеют одинаковую массу, но диаметр второго проводника в 3 раза больше, чем первого. Во сколько раз будут отличаться силы тока в проводниках, если их подключить к одинаковым источникам тока?


 Получите свидетельство
Получите свидетельство Вход
Вход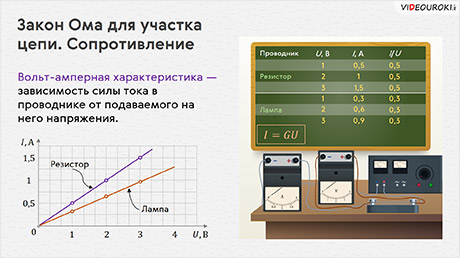




 7651
7651

