Вопросы занятия:
· поговорить о равенстве и подобии треугольников;
· сформулировать и доказать три признака равенства треугольников;
· сформулировать и доказать три признака подобия треугольников.
Материал урока
Напомним, что две фигуры называют равными, если их можно совместить.
Давайте, возьмём два равных треугольника  и
и
 .
И наложим их друг на друга.
.
И наложим их друг на друга.
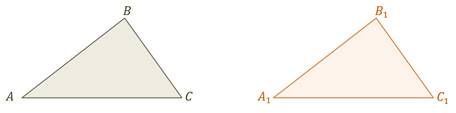
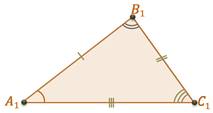
Видим, они совместились, то есть попарно совместились их вершины и стороны. А значит, попарно совместились и углы этих треугольников.
Следовательно, можем сделать вывод: если два треугольника равны, то стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника.
Также следует отметить, что в равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот: против соответственно равных углов лежат равные стороны.
Равенство треугольников 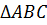 и
и
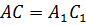 обозначают
следующим образом:
обозначают
следующим образом:

И говорят «треугольник А Б Ц равен треугольнику А1 Б1 Ц1».
Исходя из рассмотренного, можно сказать, что равенство треугольников мы можем установить не только наложением их друг на друга, но и сравнивая их элементы.
Для установления равенства треугольников пользуются соответствующими признаками равенства треугольников.
Итак, первый признак равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Докажем это утверждение. Пусть 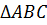 и
и
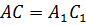 –
треугольники, у которых
–
треугольники, у которых  ,
,
 ,
,
 .
Докажем, что
.
Докажем, что  .
.

Так как  ,
то
,
то  совместится
с
совместится
с  ,
а
,
а  и
и
 совместятся
с лучами
совместятся
с лучами  и
и
 .
.
Так как  ,
а
,
а  ,
то
,
то  совместится
с
совместится
с  ,
а
,
а  –
с
–
с  .
Исходя из этого, точка
.
Исходя из этого, точка  совместится
с
совместится
с  ,
,
 –
с
–
с  .
Следовательно,
.
Следовательно,  совместится
с
совместится
с  .
.
Тогда имеем, треугольники 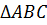 и
и
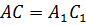 полностью
совместились. Значит,
полностью
совместились. Значит,  .
.
Таким образом, теорема доказана.
Задача.
На рисунке  ,
,
 .
Доказать, что
.
Доказать, что  .
.

Так как  ,
,
 ,
то
,
то  .
.
Рассмотрим два треугольника  и
и
 .
У
них стороны
.
У
них стороны  равны
по условию задачи. Выше мы выяснили, что
равны
по условию задачи. Выше мы выяснили, что  ,
а угол
,
а угол  –
общий угол. Следовательно, данные треугольники равны
–
общий угол. Следовательно, данные треугольники равны  по
первому признаку равенства треугольников. Значит, у них соответственные стороны
и углы равны. То есть
по
первому признаку равенства треугольников. Значит, у них соответственные стороны
и углы равны. То есть  .
Что и требовалось доказать.
.
Что и требовалось доказать.
Сформулируем второй признак равенства треугольников.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Докажем это утверждение.
Пусть 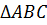 и
и
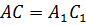 –
треугольники, у которых
–
треугольники, у которых  ,
,
 ,
,
 .
Докажем, что
.
Докажем, что  .
.

Совместим треугольник 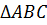 с
треугольником
с
треугольником 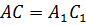 1
таким образом, чтобы вершина А совместилась с вершиной А1, сторона
АВ – с равной ей стороной А1В1, а вершины С и С1
оказались по одну сторону от прямой А1В1.
1
таким образом, чтобы вершина А совместилась с вершиной А1, сторона
АВ – с равной ей стороной А1В1, а вершины С и С1
оказались по одну сторону от прямой А1В1.
Так как  и
и
 ,
то
,
то  совместится
с
совместится
с  ,
а
,
а  –
с
–
с  .
Поэтому вершина С – общая точка сторон АС и ВС, окажется лежащей и на лучах А1С1
и В1С1, а следовательно, совместится с общей точкой этих
лучей – вершиной С1. Значит, совместятся стороны
.
Поэтому вершина С – общая точка сторон АС и ВС, окажется лежащей и на лучах А1С1
и В1С1, а следовательно, совместится с общей точкой этих
лучей – вершиной С1. Значит, совместятся стороны  и
и
 ,
,
 и
и
 .
Получаем, что треугольники
.
Получаем, что треугольники 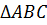 и
и
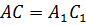 полностью
совместятся. А значит,
полностью
совместятся. А значит,  .
.
Теорема доказана.
Задача.
Отрезки  и
и
 пересекаются
в точке
пересекаются
в точке  ,
которая является серединой отрезка
,
которая является серединой отрезка  ,
а
,
а  .
Доказать, что
.
Доказать, что  .
.

Рассмотрим  и
и
 .
У них
.
У них  ,
так как Е – середина отрезка АВ. Углы
,
так как Е – середина отрезка АВ. Углы  равны
по условию задачи. А углы
равны
по условию задачи. А углы  равны
как вертикальные. Получаем, что треугольники
равны
как вертикальные. Получаем, что треугольники  равны
по второму признаку.
равны
по второму признаку.
Прежде чем сформулировать третий признак равенства треугольников, давайте немного подробнее поговорим о равнобедренных треугольниках.
Напомним, что треугольник называется равнобедренным, если две его стороны равны.

Возьмём, к примеру, треугольник 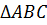 ,
у которого стороны
,
у которого стороны  .
Как мы уже отмечали, эти стороны называют боковыми сторонами. Третья
сторона
.
Как мы уже отмечали, эти стороны называют боковыми сторонами. Третья
сторона  называется
основанием равнобедренного треугольника. Точка
называется
основанием равнобедренного треугольника. Точка  называется
вершиной равнобедренного треугольника, а точки
называется
вершиной равнобедренного треугольника, а точки  и
и
 –
вершинами при его основании. Угол
–
вершинами при его основании. Угол  называется
углом при вершине, а углы
называется
углом при вершине, а углы  и
и
 –
углами при основании.
–
углами при основании.
Теперь сформулируем некоторые теоремы о свойствах равнобедренного треугольника.
Первая теорема звучит следующим образом: в равнобедренном треугольнике углы при основании равны.
И вторая теорема: в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Ну а теперь давайте перейдём к третьему признаку равенства треугольников.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Докажем это утверждение.
Пусть 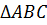 и
и
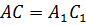 –
два треугольника, у которых
–
два треугольника, у которых  ,
,
 ,
,
 .
Докажем, что
.
Докажем, что  .
.
Приложим треугольник 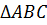 к
треугольнику
к
треугольнику 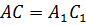 таким
образом, чтобы вершина А совместилась с вершиной А1, вершина В – с
вершиной В1, а вершины С и С1 оказались по разные стороны
от прямой А1В1. Тогда возможны три случая.
таким
образом, чтобы вершина А совместилась с вершиной А1, вершина В – с
вершиной В1, а вершины С и С1 оказались по разные стороны
от прямой А1В1. Тогда возможны три случая.
Рассмотрим первый случай.

Так как по условию теоремы 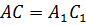 ,
,
 ,
то треугольники
,
то треугольники  и
и
 являются
равнобедренными. По теореме о свойстве углов равнобедренного треугольника
являются
равнобедренными. По теореме о свойстве углов равнобедренного треугольника  ,
,
 .
Поэтому
.
Поэтому  .
.
Итак мы знаем, что 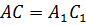 ,
,
 и
и
 .
Следовательно, треугольник
.
Следовательно, треугольник  по
первому признаку равенства треугольников.
по
первому признаку равенства треугольников.
Рассмотрим второй случай.

Так как по условию теоремы 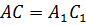 ,
то треугольник
,
то треугольник  является
равнобедренным. По теореме о свойстве углов равнобедренного треугольника углы
при основании
является
равнобедренным. По теореме о свойстве углов равнобедренного треугольника углы
при основании  .
Можем сказать, что треугольники
.
Можем сказать, что треугольники  по
первому признаку равенства треугольников, так как
по
первому признаку равенства треугольников, так как 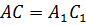 ,
,
 ,
,
 .
.
И третий случай.

По условию теоремы 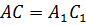 и
и
 .
Из этого следует, что треугольники
.
Из этого следует, что треугольники  и
и
 являются
равнобедренными. Тогда по теореме о свойстве углов при основании
равнобедренного треугольника
являются
равнобедренными. Тогда по теореме о свойстве углов при основании
равнобедренного треугольника  .
А, следовательно,
.
А, следовательно,  .
Итак, треугольники
.
Итак, треугольники  по
первому признаку равенства треугольников, так как
по
первому признаку равенства треугольников, так как 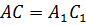 и
и
 по
условию теоремы, а
по
условию теоремы, а  .
.
Теорема доказана.
Задача.
Отрезок  –
общее основание равнобедренных
–
общее основание равнобедренных  и
и .
Докажите, что
.
Докажите, что  .
.

Доказательство.
Рассмотрим треугольники  и
и
 .
У этих треугольников
.
У этих треугольников  ,
,
 ,
а сторона
,
а сторона  –
общая. Тогда получаем, что треугольники
–
общая. Тогда получаем, что треугольники  по
третьему признаку равенства треугольников.
по
третьему признаку равенства треугольников.
Что и требовалось доказать.
Теперь перейдём к признакам подобия треугольников.
Вспомним, что подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.

Подобные треугольники обозначают следующим образом:  .
.
Сформулируем первый признак подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство.
Пусть у треугольников  и
и

 ,
,
 .
.
Напомним, что сумма углов треугольника равна 180о. Значит, для наших треугольников можем записать следующие равенства:

Выразим из первого равенства  ,
а из второго – угол
,
а из второго – угол  .
Так как по условию
.
Так как по условию  ,
,
 ,
то, следовательно,
,
то, следовательно,  .
То есть у рассматриваемых треугольников углы соответственно равны.
.
То есть у рассматриваемых треугольников углы соответственно равны.
Теперь докажем, что сходственные стороны этих треугольников пропорциональны.
Так как  ,
то по теореме: если угол одного треугольника равен углу другого треугольника,
то площади этих треугольников относятся как произведения сторон, заключающих
равные углы; площадь треугольника
,
то по теореме: если угол одного треугольника равен углу другого треугольника,
то площади этих треугольников относятся как произведения сторон, заключающих
равные углы; площадь треугольника  .
.
Углы  ,
а тогда отношение площадей наших треугольников равно
,
а тогда отношение площадей наших треугольников равно  .
.
Заметим, что у этих равенств левые части одинаковые, а тогда можно приравнять их правые части:

Упростим, получившееся равенство. Для этого обе части
равенства разделим на  ,
а затем умножим на
,
а затем умножим на  .
И получим,
.
И получим,

Аналогично, так как  ,
,
 ,
то имеют место следующие равенства:
,
то имеют место следующие равенства:

Их левые части равны, а тогда можем приравнять их правые части. Упростим, получившееся равенство. И получим,

Таким образом, из полученных равенств следует  .
.
То есть мы получили, что сходственные стороны
треугольников  и
и
 пропорциональны.
Выше мы доказали, что соответственные углы этих треугольников равны, а значит,
пропорциональны.
Выше мы доказали, что соответственные углы этих треугольников равны, а значит,  .
.
Что и требовалось доказать.
Задача.
На рисунке:  см,
см,
 см,
см,
 см,
а
см,
а  .
Найти
.
Найти  .
.

Рассмотрим треугольники  и
и
 .
У них углы
.
У них углы  по
условию задачи, а
по
условию задачи, а  –
общий. Значит,
–
общий. Значит,  по
первому признаку.
по
первому признаку.
Из подобия треугольников следует пропорциональность их
сходственных сторон:  .
Подставим известные значения сторон из условия задачи:
.
Подставим известные значения сторон из условия задачи:  .
Выразим
.
Выразим  .
Запишем ответ.
.
Запишем ответ.
Сформулируем и докажем второй признак подобия треугольников.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.

Рассмотрим треугольники  и
и
 ,
у которых
,
у которых  ,
,
 .
.
Построим на стороне  треугольника
треугольника
 треугольник
треугольник
 ,
у которого
,
у которого  ,
,
 .
Тогда треугольники
.
Тогда треугольники  по
первому признаку. Для сходственных сторон можем записать, что
по
первому признаку. Для сходственных сторон можем записать, что  .
.
По условию,  .
А тогда их этих двух равенств получим, что
.
А тогда их этих двух равенств получим, что  .
.
Рассмотрим треугольники  и
и
 .
У них
.
У них  .
Сторона
.
Сторона  –
общая.
–
общая.  ,
так как
,
так как  и
и
 .
А значит, треугольники
.
А значит, треугольники  по
двум сторонам и углу между ними, то есть по первому признаку равенства
треугольников.
по
двум сторонам и углу между ними, то есть по первому признаку равенства
треугольников.
Таким образом, мы получили, что треугольник  ,
а построенный треугольник
,
а построенный треугольник  .
Отсюда следует, что треугольник
.
Отсюда следует, что треугольник  .
.
Что и требовалось доказать.
Задача.
На одной из сторон  отложены
отрезки
отложены
отрезки  и
и
 ,
равные соответственно
,
равные соответственно  см
и
см
и  см.
На другой стороне этого же угла отложены отрезки
см.
На другой стороне этого же угла отложены отрезки  и
и
 ,
соответственно равные
,
соответственно равные  см
и
см
и  см.
Подобны ли
см.
Подобны ли  и
и
 ?
?

Рассмотрим треугольники  и
и
 .
У них
.
У них  –
общий. Составим отношения сторон
–
общий. Составим отношения сторон  ,
,
 ,
образующих
,
образующих
 .
Видим, что эти отношения равны, а значит,
.
Видим, что эти отношения равны, а значит,  .
.
А, следовательно, треугольники  по
двум сторонам и углу между ними, то есть по второму признаку подобия
треугольников.
по
двум сторонам и углу между ними, то есть по второму признаку подобия
треугольников.
Ну а теперь сформулируем третий признак подобия треугольников.
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

Доказательство.
Рассмотрим треугольники  и
и
 ,
у которых стороны соответственно пропорциональны
,
у которых стороны соответственно пропорциональны  .
.
Построим на стороне  треугольника
треугольника
 треугольник
треугольник
 ,
у которого
,
у которого  ,
,
 .
.
Тогда треугольники  по
первому признаку подобия треугольников. Поэтому стороны
по
первому признаку подобия треугольников. Поэтому стороны  .
.
По условию стороны  .
Сравнивания эти равенства, получаем, что
.
Сравнивания эти равенства, получаем, что  ;
;
 .
.
Тогда треугольники  по
третьему признаку равенства треугольников, так как только что мы получили, что
по
третьему признаку равенства треугольников, так как только что мы получили, что  ;
;
 ,
а сторона
,
а сторона  у
них общая. Следовательно, у этих треугольников углы соответственно равны, то
есть
у
них общая. Следовательно, у этих треугольников углы соответственно равны, то
есть  .
А так как
.
А так как  ,
то
,
то  .
.
Таким образом, мы получаем, что у треугольников  и
и
 стороны
пропорциональны и
стороны
пропорциональны и  .
Следовательно,
.
Следовательно,  по
второму признаку подобия треугольников.
по
второму признаку подобия треугольников.
Что и требовалось доказать.
Задача.
Выяснить, подобны ли  и
и
 ,
если
,
если  см,
см,
 см,
см,
 см,
см,
 см,
см,
 см,
см,
 см?
см?

Так как нам известны длины всех сторон данных
треугольников, то проверим, пропорциональны ли стороны треугольника  сторонам
треугольника
сторонам
треугольника  .
.
Найдём отношения сторон:

Видим, что эти отношения равны, а значит,  .
Следовательно,
.
Следовательно,  по
третьему признаку подобия треугольников.
по
третьему признаку подобия треугольников.
Итоги урока
На этом уроке мы говорили о равенстве и подобии треугольников. Сформулировали и доказали три признака равенства треугольников. А также сформулировали и доказали три признака подобия треугольников.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 2855
2855

