Вопросы занятия:
· назвать элементы треугольника;
· доказать, что медианы треугольника пересекаются в одной точке;
· доказать, что биссектрисы треугольника также пересекаются в одной точке;
· доказать, что высоты или прямые, содержащие высоты, пересекаются в одной точке.
Материал урока
Треугольник – это одна из самых замечательных и самых важных фигур в геометрии.
Итак, давайте отметим три точки А, В и С, которые не лежат на одной прямой, и соединим их отрезками. В результате получим геометрическую фигуру, которая и называется треугольником.
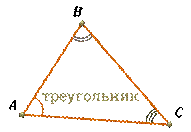
Точки 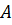 ,
,
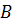 ,
,
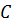 –
вершины треугольника, а отрезки
–
вершины треугольника, а отрезки 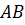 ,
,
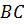 и
и
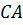 –
стороны треугольника.
–
стороны треугольника.
Треугольник, который мы с вами построили, обозначают так:
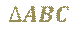
И говорят «треугольник А Б Ц».
Поменяв буквы местами, этот же треугольник можно обозначить и таким образом:
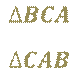
Углы 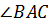 ,
,
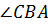 ,
,
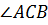 называют
углами
называют
углами  .
.
Кстати, углы треугольника можно обозначать и одной латинской буквой: например, ∠𝐴, ∠𝐵, ∠𝐶.
Сумма длин всех сторон треугольника называется периметром
треугольника. Т.е. периметр нашего треугольника равен 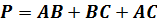 .
.
Различают следующие виды треугольников:
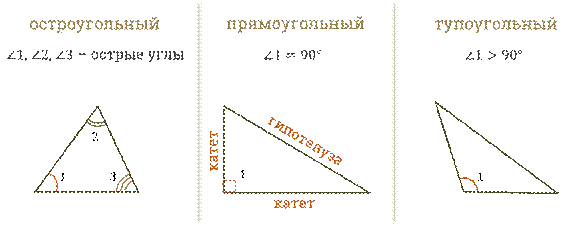
- в зависимости от величины углов:
остроугольный (все углы треугольника острые, т.е. меньше 90о);
прямоугольный (один из углов треугольника прямой, т.е. равен 90о);
Нужно помнить, что стороны прямоугольного треугольника имеют специальные названия. Итак, две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
И третий вид треугольников: тупоугольный (один из углов треугольника тупой, т.е. больше 90о).
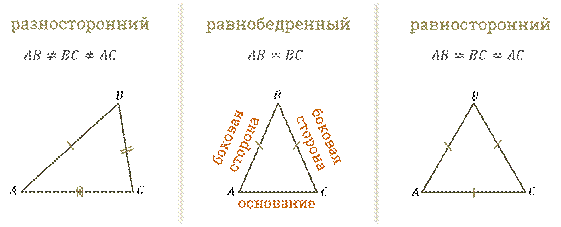
Затем, треугольники различают в зависимости от величины сторон:
разносторонний (все стороны разной длины);
равнобедренный (две стороны равны и называются боковыми, а третья сторона – основанием);
и равносторонний (все стороны равны между собой).
Во всяком треугольнике против большей стороны лежит больший угол; против равных сторон – равные углы. Любая сторона треугольника меньше суммы и больше разности двух других сторон.
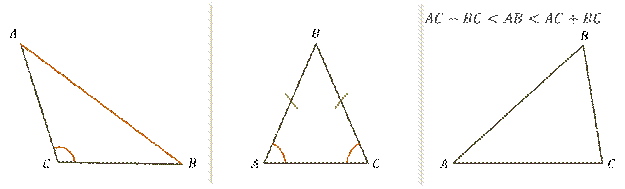
Определение.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Любой треугольник имеет три медианы. Например,
возьмём треугольник  .
Если точки
.
Если точки 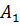 ,
,
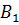 и
и
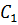 –
соответственно середины сторон
–
соответственно середины сторон 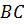 ,
,
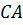 и
и
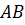 ,
то отрезки
,
то отрезки 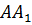 ,
,
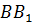 и
и
 –
медианы этого треугольника.
–
медианы этого треугольника.
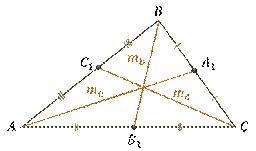
Медианы, проведённые из
вершин  ,
,
 и
и
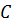 (или
их длины) треугольника
(или
их длины) треугольника  можно
обозначить:
можно
обозначить:
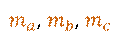
Определение.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны.
Любой треугольник имеет три биссектрисы.
Возьмём некоторый треугольник  и
проведём биссектрису
и
проведём биссектрису 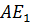 угла
угла
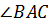 ,
,
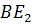 –
угла ∠𝐴𝐵𝐶
и
–
угла ∠𝐴𝐵𝐶
и 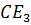 –
угла
–
угла 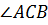 .
.
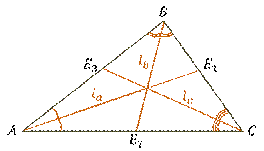
Биссектрисы, проведённые из вершин 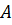 ,
,
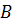 и
и
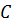 (или
их длины) треугольника
(или
их длины) треугольника  можно
обозначить:
можно
обозначить:
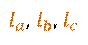
Определение.
Высотой треугольника называется перпендикуляр, проведённый из его вершины к прямой, содержащей противоположную сторону.
Каждый треугольник имеет три высоты. Изобразим
треугольник  и
отрезки
и
отрезки 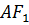 ,
,
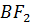 и
и
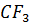 ,
которые являются высотами нашего треугольника.
,
которые являются высотами нашего треугольника.
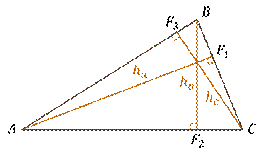
Высоты, проведённые из вершин 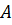 ,
,
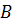 и
и
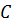 (или
их длины) треугольника
(или
их длины) треугольника  можно
обозначить:
можно
обозначить:
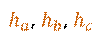
Определение.
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
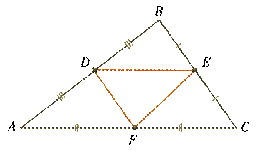
Поскольку в любом треугольнике три стороны, то треугольник имеет три средние линии. Средняя линия треугольника, соединяющая две данные стороны, параллельна третьей стороне, а её длина равна половине этой стороны.
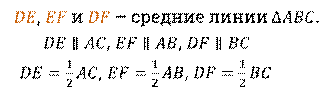
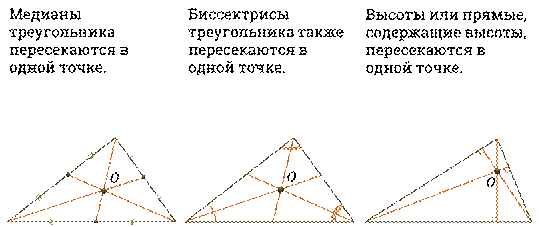
Отметим свойства, которыми обладают медианы, биссектрисы и высоты треугольника.
Медианы треугольника пересекаются в одной точке.
Биссектрисы треугольника также пересекаются в одной точке.
Высоты или прямые, содержащие высоты, пересекаются в одной точке.
Докажем каждое из этих свойств по очереди.
Итак, три медианы треугольника пересекаются в одной
точке, которая делит каждую медиану в отношении 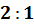 ,
считая от вершины.
,
считая от вершины.
Доказательство.
Рассмотрим треугольник  .
Пересечение медиан
.
Пересечение медиан 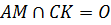 следует
из того, что
следует
из того, что 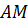 – внутренний луч
– внутренний луч 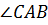 ;
; 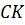 –
внутренний луч
–
внутренний луч 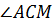 .
.
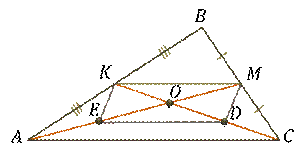
Тогда отрезок 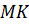 является
средней линией треугольника
является
средней линией треугольника  .
Значит,
.
Значит, 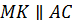 и
и
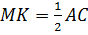 .
.
Обозначим середины отрезков 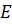 –
середина
–
середина 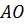 ,
,
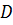 –
середина
–
середина 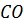 ,
тогда
,
тогда 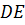 –
средняя линия
–
средняя линия 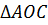 .
Следовательно,
.
Следовательно, 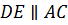 и
и
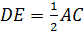 .
Таким образом,
.
Таким образом, 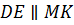 и
и
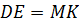 ,
следовательно, четырёхугольник
,
следовательно, четырёхугольник 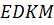 –
параллелограмм, диагонали которого
–
параллелограмм, диагонали которого 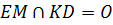 и
делятся этой точкой пополам, т.е.
и
делятся этой точкой пополам, т.е. 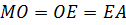 и
и
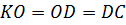 .
.
Но тогда 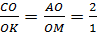 .
.
Что и требовалось доказать.
Биссектрисы треугольника пересекаются в одной точке.
Доказательство.
Рассмотрим треугольник  .
.
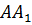 и
и
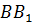 биссектрисы
треугольника. Обозначим буквой О точку их пересечения. Давайте из этой точки
проведём перпендикуляры
биссектрисы
треугольника. Обозначим буквой О точку их пересечения. Давайте из этой точки
проведём перпендикуляры 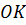 ,
,
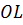 и
и
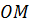 соответственно
к прямым
соответственно
к прямым 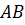 ,
,
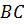 и
и
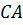 .
.
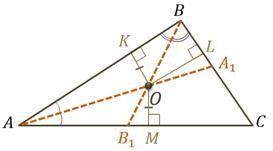
Ранее мы с вами доказали теорему о свойстве точек биссектрисы неразвёрнутого угла. Из этой теоремы следует, что
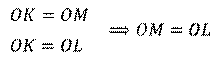
Т.е. точка О равноудалена от сторон угла 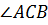 .
Значит, лежит на биссектрисе
.
Значит, лежит на биссектрисе 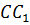 этого
угла. Следовательно, все три биссектрисы треугольника
этого
угла. Следовательно, все три биссектрисы треугольника  пересекаются
в точке О.
пересекаются
в точке О.
Что и требовалось доказать.
Высоты треугольника (или их продолжения) пересекаются в одной точке.
Докажем это утверждение.
Рассмотрим произвольный треугольник  .
Нам нужно доказать, что прямые
.
Нам нужно доказать, что прямые 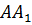 ,
,
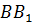 и
и
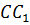 ,
содержащие его высоты, пересекаются в одной точке.
,
содержащие его высоты, пересекаются в одной точке.
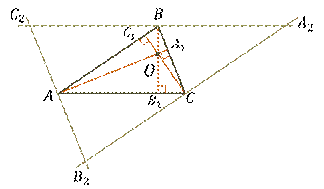
Для этого проведём через каждую вершину треугольника  прямую,
параллельную противоположной стороне. Т.е. через вершину
прямую,
параллельную противоположной стороне. Т.е. через вершину 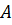 проведём
прямую параллельную стороне
проведём
прямую параллельную стороне 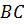 .
Через вершину
.
Через вершину 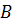 –
прямую параллельную стороне
–
прямую параллельную стороне 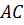 .
А через вершину
.
А через вершину 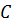 –
прямую параллельную стороне
–
прямую параллельную стороне 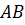 .
Смотрите, у нас получился новый треугольник с вершинами
.
Смотрите, у нас получился новый треугольник с вершинами 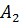 ,
,
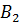 и
и
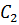 .
Рассмотрим его свойства.
.
Рассмотрим его свойства. 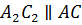 ,
значит, и
,
значит, и 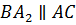 .
.
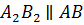 .
Значит, и
.
Значит, и 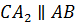 .
Следовательно, четырёхугольник
.
Следовательно, четырёхугольник 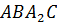 является
параллелограммом. Мы знаем, что противоположные стороны параллелограмма попарно
равны. Значит,
является
параллелограммом. Мы знаем, что противоположные стороны параллелограмма попарно
равны. Значит, 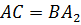 ,
,
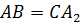 .
.
Аналогично,

Следовательно, четырёхугольник 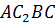 является
параллелограммом. Значит,
является
параллелограммом. Значит, 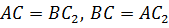 .
Таким образом, точка
.
Таким образом, точка 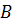 является
серединой отрезка
является
серединой отрезка 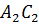 .
Следовательно, высота
.
Следовательно, высота 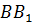 –
серединный перпендикуляр
–
серединный перпендикуляр 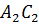 .
.
Аналогично точка 𝐴
является серединой отрезка 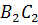 и
высота
и
высота 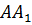 –
серединный перпендикуляр
–
серединный перпендикуляр 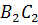 .
Точка
.
Точка 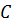 является
серединой отрезка
является
серединой отрезка 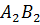 и
высота
и
высота 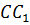 –
серединный перпендикуляр
–
серединный перпендикуляр 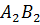 .
.
Мы знаем, что серединные перпендикуляры к сторонам
треугольника пересекаются в одной точке. Значит, и наши серединные
перпендикуляры 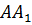 ,
,
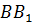 и
и
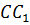 ,
проведённые к сторонам большого треугольника
,
проведённые к сторонам большого треугольника 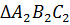 ,
пересекаются в одной точке. Обозначим её буквой О. Также мы показали, что эти
же серединные перпендикуляры являются и высотами маленького треугольника
,
пересекаются в одной точке. Обозначим её буквой О. Также мы показали, что эти
же серединные перпендикуляры являются и высотами маленького треугольника  .
Значит, высоты треугольника
.
Значит, высоты треугольника  пересекаются
в одной точке, в точке О.
пересекаются
в одной точке, в точке О.
Что и требовалось доказать.
А теперь рассмотрим решения нескольких задач.
Задача.
Периметр треугольника равен 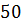 см.
Одна сторона больше другой на
см.
Одна сторона больше другой на 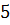 см
и меньше третьей на
см
и меньше третьей на 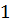 см.
Найдите стороны треугольника.
см.
Найдите стороны треугольника.
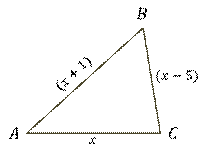
Пусть одна сторона треугольника равна 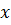 см,
тогда другая будет
см,
тогда другая будет 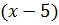 см,
а третья
см,
а третья 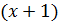 см.
Известно, что периметр треугольника равен 50 см. Составим уравнение:
см.
Известно, что периметр треугольника равен 50 см. Составим уравнение:
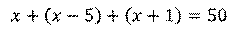
Решим это уравнение. Получим,
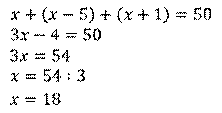
Тогда имеем одна сторона треугольника 18 см, вторая 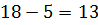 (см)
и третья
(см)
и третья 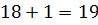 (см).
Не забудем записать ответ.
(см).
Не забудем записать ответ.
Задача.
В равнобедренном треугольнике найти неизвестные
стороны, если отношение боковой стороны к основанию равно  ,
а периметр равен
,
а периметр равен 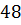 см.
см.
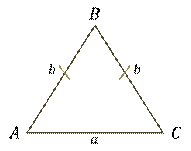
Пусть а – основание, 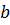 –
боковая сторона равнобедренного треугольника, тогда
–
боковая сторона равнобедренного треугольника, тогда 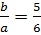 .
Отсюда,
.
Отсюда, 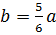 .
Тогда периметр треугольника будет равен:
.
Тогда периметр треугольника будет равен:
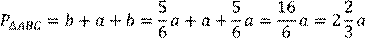
Заменим 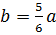 .
Приведём подобные и получим, что периметр равен:
.
Приведём подобные и получим, что периметр равен:
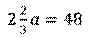
Составим уравнение. Решим его. Тогда получим, что
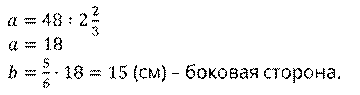
Запишем ответ.
Задача.
Дан треугольник, стороны которого соответственно равны
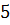 ,
,
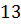 и
и
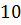 см.
Найти периметр треугольника, вершинами которого являются середины сторон
данного треугольника.
см.
Найти периметр треугольника, вершинами которого являются середины сторон
данного треугольника.
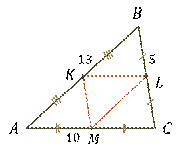
Пусть дан треугольник  .
Точки
.
Точки 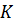 ,
,
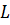 и
и
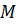 —
середины сторон
—
середины сторон 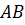 ,
,
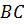 и
и
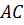 ,
соответственно.
,
соответственно.
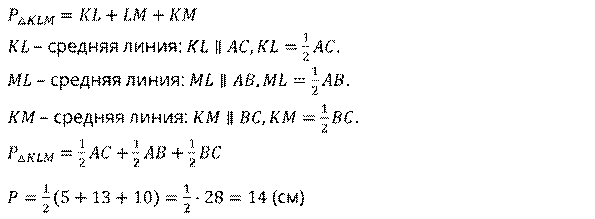
Запишем ответ.
Итоги урока
На этом уроке мы говорили о треугольниках. Рассмотрели их элементы. А также доказали, что медианы треугольника пересекаются в одной точке. Биссектрисы треугольника также пересекаются в одной точке. Высоты или прямые, содержащие высоты, пересекаются в одной точке.

 Получите свидетельство
Получите свидетельство Вход
Вход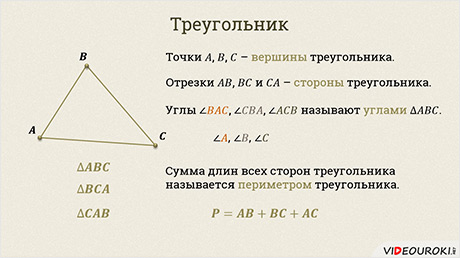



 2
2 4040
4040





Повторяем тему" Треугольник"
jnkbxyj