Уравнение окружности. Взаимное расположение окружностей на плоскости

Вопросы занятия:

·  вспомнить, какой вид имеет уравнение окружности с центром в точке с координатами (x₀; y₀) и радиусом r;

·  повторить вид уравнения окружности с центром вначале координат и радиусом r;

·  вспомнить, как могут располагаться две окружности на плоскости.

Материал урока

Начнём с того, что вспомним, как мы выводили уравнение окружности с центром в точке с координатами (x₀; y₀) и радиусом r.

Пусть центр окружности имеет координаты:

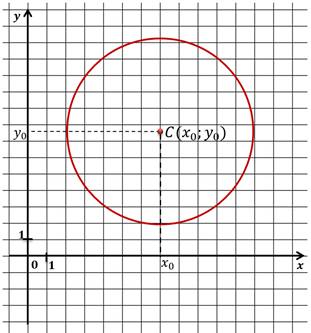
Возьмём на окружности произвольную точку. Запишем формулу расстояния между точками.

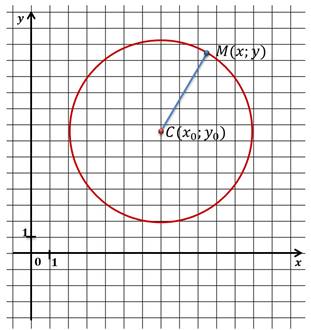
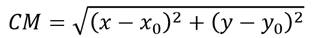
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с центром окружности – это радиус.

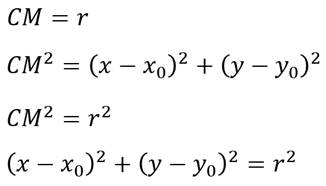
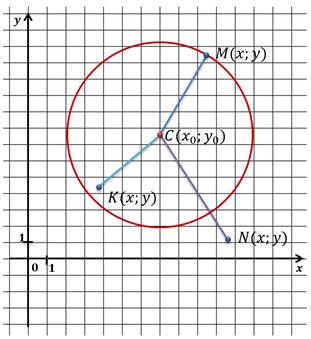
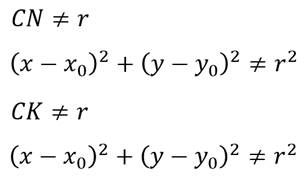
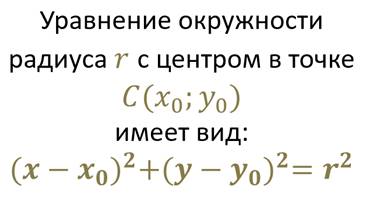
Рассмотрим задачу.

Пример.

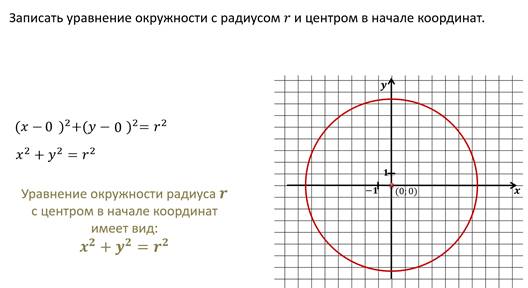
Пример.

Рассмотрим ещё одну задачу.

Пример.

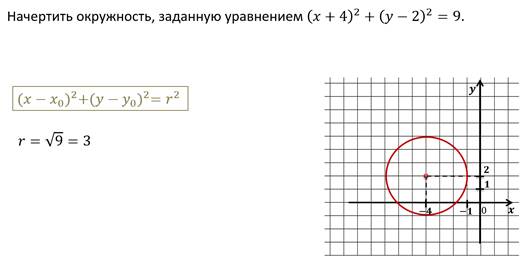
Пример.

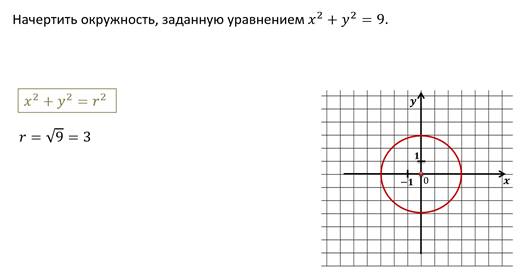
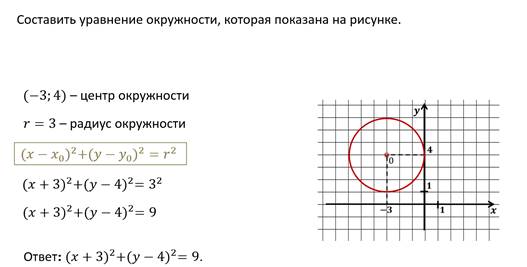
Теперь давайте попробуем решить задачу обратную данным. То есть по рисунку составить уравнение окружности.

Пример.

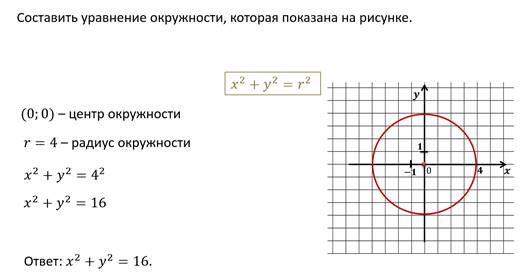
Решим ещё одну задачу.

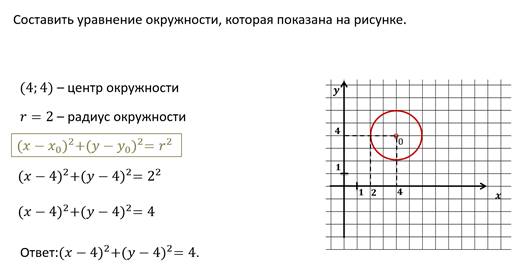
Решим ещё одну задачу.

Решая задачи мы с вами выполняли один и тоже порядок действий. Давайте ещё раз повторим этот порядок.

Для того, что бы составить уравнение окружности и построить ее надо:

1. Найти координаты центра окружности.

2. Найти длину радиуса этой окружности.

3. Записать уравнение окружности.

4. Подставить полученные значения в уравнение окружности.

5. Построить окружность, если это требуется для решения задачи.

Рассмотрим ещё одну задачу.

Пример.

Теперь давайте вспомним, как две окружности могут располагаться на плоскости.

Сначала перечислим все возможные случаи взаимного расположения.

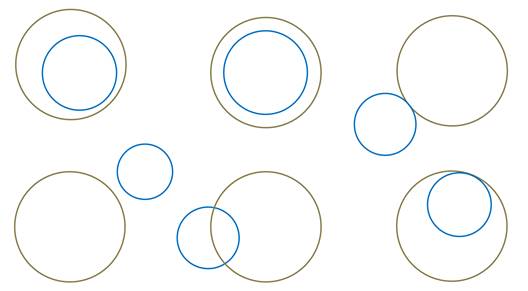
Сначала рассмотрим случай, когда центры окружностей совпадают.

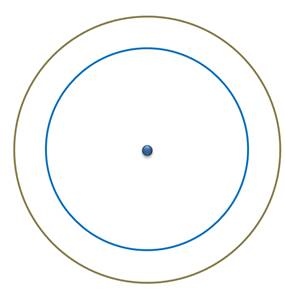
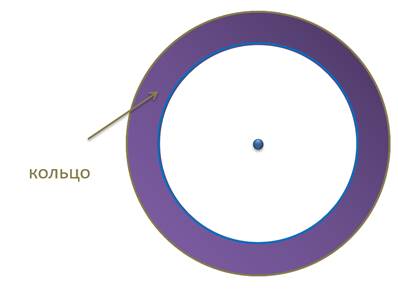
Такие окружности называются концентрическими. Если радиусы окружностей не равны, то такие окружности образуют кольцо. Если радиусы окружностей равны, то окружности совпадают.

Теперь давайте рассмотрим случаи, когда центры окружностей не совпадают. Соединим их прямой d, которую назовём линией центров данной пары окружностей.

В данном случае взаимное расположение окружностей будет зависеть от соотношения между величиной d и величинами радиусов окружностей. Для того, чтобы было понятно о какой окружности идёт речь, радиус одной из окружностей обозначим за r, а радиус второй окружности – за R. И будем считать, что r ≤ R.

Если d > r+ R, то очевидно, что окружности не пересекаются. В этом случае говорят, что одна окружность лежит вне другой.

Если d < R – r, то тогда одна окружность лежит внутри другой, но они не пересекаются.

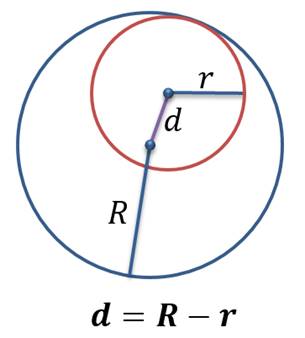
Если d = R – r, тогда малая окружность лежит внутри большой, но имеет с ней одну общую точку на линии центров. Такой случай называют внутренним касанием, а такие окружности называют внутренне касающимися.

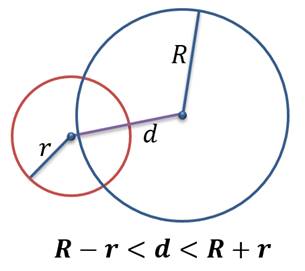
Если R – r < d < R +r, то окружности пересекаются в двух точках и называются пересекающимися.

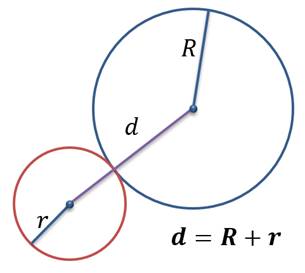
Если d = R +r, то такие окружности имеют одну общую точку, причём центр одной из них расположен за пределами второй окружности. Такой вид касания называется внешним касанием, а такие окружности называются внешне касающимися. Точка касания внешне касающихся окружностей лежит на линии центров.

Решим несколько задач.

Пример.

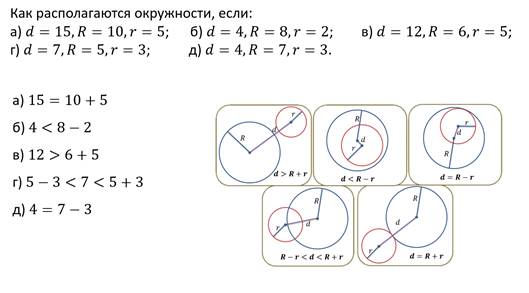
Рассмотрим ещё одну задачу.

Пример.

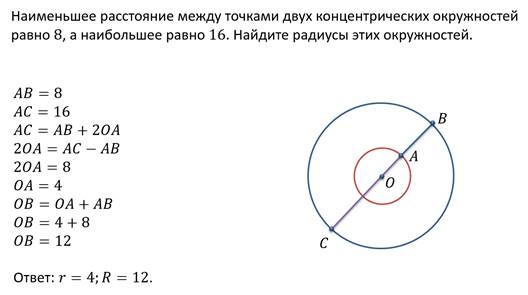
Решим ещё одну задачу.

Решим ещё одну задачу.

Итоги урока

Сегодня на уроке мы с вами вспомнили какой вид имеет уравнение окружности с центром в точке с координатами (x₀; y₀) и радиусом r. Повторили вид уравнения окружности с центром вначале координат и радиусом r. Вспомнили как могут располагаться две окружности на плоскости.