Вопросы занятия:
· вывести уравнения прямой и произвольной линии на плоскости.
Материал урока
И начнём мы наш урок с повторения уравнения прямой.
В координатной плоскости прямая может располагаться либо вертикально (параллельно оси Oy), горизонтально (параллельно оси Ox) либо быть наклонной к обеим осям.

Первым давайте рассмотрим случай, когда прямая параллельна оси Oy.
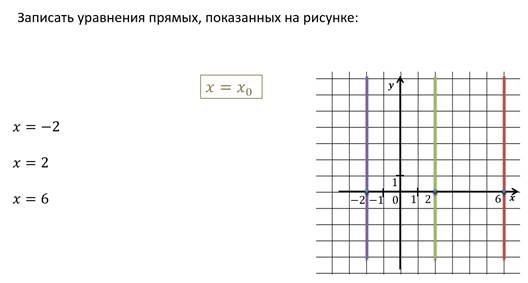
Возьмём на оси Ox, например, точку с координатой 3 и проведём через эту точку прямую, параллельную оси Oy. Абсцисса любой точки этой прямой равна 3. То есть координаты любой точки этой прямой удовлетворяют уравнению x = 3, а координаты любой точки, которая не лежит на данной прямой не удовлетворяют данному уравнению. Значит, уравнение x = 3 является уравнением прямой параллельной оси Oy и проходящей через точку с координатами (3; 0).

Можно сказать, что произвольная прямая параллельная оси Oy задаётся уравнением:

Ось Oy задаётся уравнением x = 0.
Решим задачу.
Задача.
Рассмотрим теперь случай, когда прямая параллельна оси Ox.
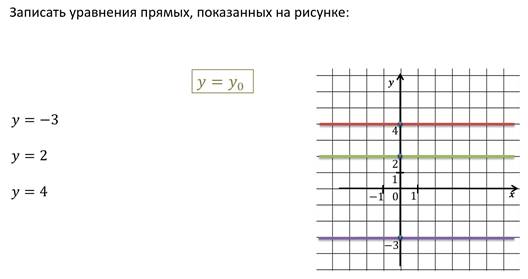
Возьмём на оси Oy, например, точку 5 и проведём через неё прямую параллельную оси Ox. Любая точка этой прямой удовлетворяет уравнению y = 5, любая точка, которая не лежит на этой прямой не удовлетворяет этому уравнению, значит, эту прямую задаёт уравнение y = 5.

Можно сказать, что произвольная прямая параллельная оси Ox задаётся уравнением:

Ось Ox задаётся уравнением y = 0.
Решим задачу.
Задача.
Теперь рассмотрим случай, когда прямая наклонная к обеим осям.
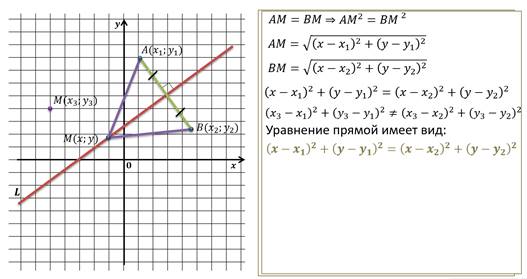
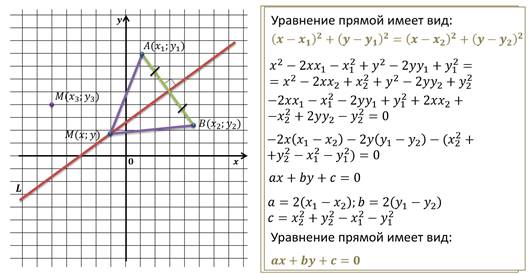
Решим задачу.
Задача.
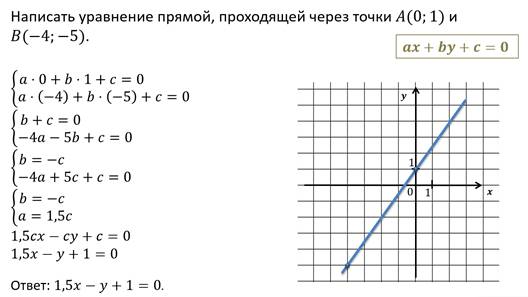
Запишем общее уравнение прямой.

Предположим, что:

Выразим y через x:

Получили уравнение

Число k называется угловым коэффициентом прямой.
Отметим, что две параллельные прямые, не параллельные оси Oy имеют одинаковые угловые коэффициенты и если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны. Почему мы говорим о прямых, не параллельных оси Oy? Потому что, мы помним, что уравнение прямых, параллельных оси имеют вид x = x0, и они все параллельны между собой.
Решим несколько задач.
Пример.

Решим ещё одну задачу.
Пример.

Пример.

Теперь давайте вспомним как мы вводили понятие уравнения для произвольной линии.
Пусть в декартовой системе координат дана произвольная линия L.

Уравнение с двумя переменными x и y называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Например,

Давайте решим задачу.
Пример.

Рассмотрим ещё один пример.

Решим ещё одну задачу.

Итоги урока
Сегодня на уроке мы с вами повторили уравнения прямой и произвольной линии на плоскости.

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 2082
2082

