Понятие о письменном приёме деления на однозначное число

Привет, ребята!

Сегодня я хочу рассказать вам о письменном приёме деления на однозначное число. Вы уже встречались с подобной записью деления, когда знакомились с темой «Деление с остатком». Но сегодня мы с вами поговорим об этом подробнее и выполним несколько упражнений на закрепление деления столбиком. Итак, приступим.

Давайте вспомним, как можно устно делить двузначное число на однозначное. Вот, к примеру, девяносто шесть разделить на три. Представим число девяносто шесть в виде суммы разрядных слагаемых – девяносто и шесть. Теперь каждое из них делим на делитель – три. Получается тридцать и два. Складываем эти частные. Ответ: тридцать два. Точно так же можно разделить и трёхзначное число. Разделим на три число триста девяносто шесть. Раскладываем число триста девяносто шесть на сумму разрядных слагаемых – триста, девяносто и шесть. Делим каждое из них на три. Получается сто, тридцать и два. Складываем эти частные. Ответ: сто тридцать два.

Да-а, длинная запись получилась. А вот как это вычисление можно выполнить столбиком.

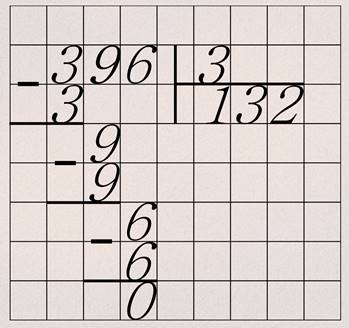
Пишем делимое – триста девяносто шесть. Отступив одну клеточку вправо пишем делитель – три. Отделяем делимое от делителя вертикальной чертой и под делителем проводим горизонтальную черту. Получилась лежащая на боку буква Т. Под горизонтальной чертой будет место для ответа – частного.

Деление столбиком, в отличие от остальных арифметических действий, мы начинаем не с единиц, а с наибольшего разряда делимого. В нашем числе это сотни. Три сотни делим на три. Предположим, что получится один. Единицу запишем под горизонтальной чертой. Ну а вдруг я ошибся, и получится не один, а какое-то другое число? Проверить это можно умножением. Умножаю один на три. Получается три. Всё верно. Результат умножения записываю под сотнями делимого. А теперь подчёркиваю и вычитаю из верхней тройки нижнюю. Получается нуль.

Но не спешите его записывать. Пока деление не закончим, нули писать не надо. Сотни разделили, теперь будем делить десятки. Для этого перенесём десятки из делимого под черту, но не левее и не правее, а строго под цифрой десятков в делимом. Девять десятков делим на три. Я думаю, что получится два. Записываю двойку в частное, и обязательно проверю. А вдруг что-то напутал? Умножаю двойку из частного на делитель – три. Это шесть. Подписываю под вот этой девяткой. Черта. Вычитаю из девяти девять. Получается три. Да. Вот и ошибка! При вычитании получился остаток, равный делителю. А ведь вы умеете выполнять деление с остатком и знаете, что остаток обязательно должен быть меньше делителя – не больше, не равен, а именно меньше.

Ну и ну! Какую глупую ошибку я допустил! Ведь при делении девяти на три должно получится число три. Как хорошо, что деление я проверил умножением! Три из частного умножаю на делитель три, получается девять. Вычитаю. Теперь в остатке нуль, который я опять не записываю – ведь мы ещё не делили единицы.

Переходим к делению единиц. Для этого цифру, обозначающую количество единиц, переношу под новую черту, строго под единицами делимого. Делю шесть на три. Это два. Но всё-таки проверю. Умножаю двойку на делитель – три. Получилось шесть. Шестёрку записываю под вот этой шестёркой. Из шести вычитаю шесть, получится нуль. Так как закончили деление числа триста девяносто шесть, его нужно написать под чертой. Ответ: сто тридцать два.

Вы, пока слушали меня, наверное, подсмеивались. Вот ведь какой растяпа, даже три на три делит неуверенно. А когда делил девять на три вообще допустил ошибку. Да потом ещё и проверяет деление умножением. Всё в чём-то сомневается. Но ведь никто из нас не застрахован от ошибки. Бывает, на секунду отвлёкся и допустил ошибку. Что уж говорить о гораздо более трудных вычислениях. Вот поэтому при записи деления столбиком надо не только делить, но и умножать. О таких трудных случаях я расскажу вам в следующий раз. А пока давайте составим алгоритм письменного приёма деления.

Пишем делимое, и справа от него – делитель. Между ними – знак деления, похожий на лежащую на боку букву Т.

Делим сотни. Частное записываем под делителем...

Умножаем полученное частное на делитель. Произведение записываем под сотнями.

Вычитаем из сотен полученное произведение.

Переносим под черту десятки.

Делим десятки. Результат записываем в частное.

Умножаем полученное число на делитель. Произведение записываем под десятками.

Вычитаем из десятков полученное произведение.

Переносим под черту единицы.

Делим единицы. Результат записываем в частное.

Умножаем полученное число на делитель... Произведение записываем под единицами.

Вычитаем из единиц полученное произведение.

Пишем нуль.

Читаем ответ.

Уффф, какой длинный алгоритм получился. Но обратите внимание, ребята, что одни и те же действия повторяются при делении каждого разряда: делим, умножаем, вычитаем.

А теперь я предлагаю вам решить несколько примеров на деление столбиком. Не забудьте воспользоваться нашим алгоритмом.

Первый пример давайте решать вместе.

Записали число четыреста двадцать восемь и справа от него два. Вертикальная и горизонтальная черта. Делим сотни. Четыре разделить на два – два. Записали под делителем. Умножаем два на два. Это четыре. Записали под сотнями делимого. Подчёркиваем и вычитаем. Получился нуль, который мы не пишем. Из делимого вниз переносим десятки. Делим их. Один записываем в частное. Умножаем один на делитель. Полученное число два записываем под десятками. Подчёркиваем и вычитаем. Снова нуль. Его не пишем. Из делимого переносим единицы. Делим их. В частное записываем четыре. Умножаем четыре на два. Это восемь. Записываем под восьмёркой. Вычитаем. Этот нуль мы пишем, ведь деление закончено. Ответ: двести четырнадцать.

У нас есть ещё два примера. Решите их самостоятельно, а потом мы вместе проверим ответы. Будьте внимательны – пользуйтесь алгоритмом.

А теперь проверьте. Вы так решали?

Если так, то заслужили отличную отметку!

Ну что же, пришла пора нам сегодня прощаться. Но мы скоро снова встретимся. Ведь я хочу вам рассказать и о более сложных случаях деления. Так что до встречи, друзья!